Apriori算法及代码实现

原理

定义

◆ 事务T是项i的集合：$$T=\{i_a,i_b,\dots ,i_t\}$$
◆ 如果I是所有项的集合，则T是I的子集。
◆ 数据集D是T的集合。
◆ 项集：项的集合。
◆ k项集：k个项的集合。

支持度：描述发生频次
置信度：衡量规则强度

关联规则支持度：
$$SupportX\to Y=\frac{(X\cup Y)}{n}$$

◆ 关联规则置信度：
$$ConfidenceX\to Y=\frac{(X\cup Y)}{(X)}$$
$$ConfidenceX\to Y=\frac{Support(X\cup Y)}{Support(X)}$$

类似于条件概率（在Y出现的情况下X发生的概率）$$P(X|Y)=\frac{P(XY)}{P(Y)}$$

课上举的栗子：

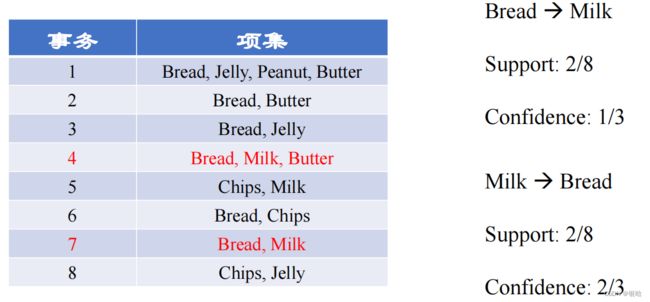
Bread -> Milk :
$$support=\frac{所有项集中出现的该项的次数}{项集总个数}$$
support：面包和牛奶一起出现的次数 = 2 ； 总项集数 = 8 ；
$$confidence=\frac{X和Y一起出现的次数}{所有项集中出现的X的次数}$$
confidence：有面包出现的项集数 = 6 ；面包牛奶一起出现的次数为2

Milk -> Bread 同理可得

---

频繁项集：支持度大于$\sigma$(最小支持度的阈值)的项集
强规则：是频繁项集且置信度大于Φ（最小置信度）

Task：给定I，D，σ和Φ，挖掘所有强规则的规则

Apriori算法过程：

1. 创建并找出所有的频繁项集
   • 从1到k挨个生成
   • 支持度大于σ认可
2. 创建并找出关联规则
   • 所有可能的关联规则
   • 关联规则的置信度大于Φ -> 认可

一个项集的子项集数: $M=2^m-1$

总项级数: $$I=\sum {}_i^N(m\ast M)$$

m : 项集数 ；N：事务数

基本思想：

• 任何非频繁项集的超集是不频繁的
• 频繁项集的所有非空子集一定是频繁的

咋一看这两条基本思想没鸟用，但是真的很有用

随着物品的增加，计算的次数呈指数的形式增长 …如果减少计数次数？
靠这两条规则

• 假设现在数据集={0，1，2，3}
• 如果 {0, 1} 是频繁的，那么 {0}, {1} 也是频繁的
• {2,3} 是 非频繁项集，那么利用上面的知识，我们就可以知道 {0,2,3} {1,2,3} {0,1,2,3} 都是 非频繁的。 也就是说，计算出 {2,3} 的支持度，知道它是 非频繁 的之后，就不需要再计算 {0,2,3} {1,2,3} {0,1,2,3} 的支持度
  

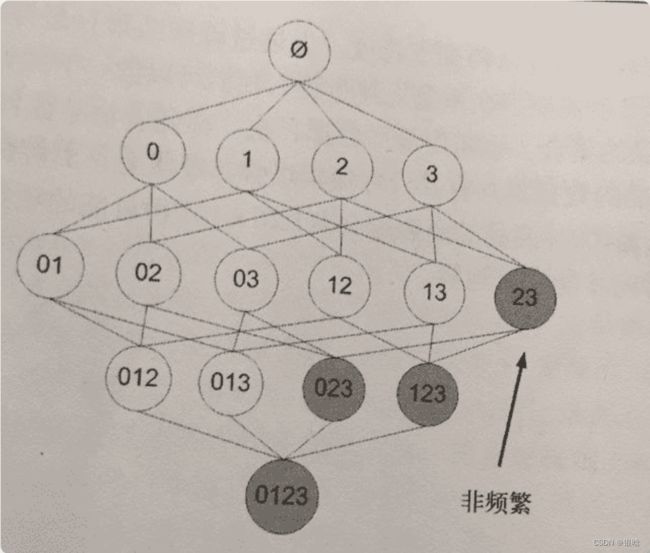
流程图：

---

代码实现

核心代码：

def returnItemsWithMinSupport(itemSet, transactionList, minSupport, freqSet):
    """
    计算子项集的支持度，返回频繁项集
    """
    _itemSet = set()
    localSet = defaultdict(int)

    for item in itemSet:
        for transaction in transactionList:
            if item.issubset(transaction):
                freqSet[item] += 1
                localSet[item] += 1

    for item, count in localSet.items():
        support = float(count) / len(transactionList)

        if support >= minSupport:
            _itemSet.add(item)

    return _itemSet


def getItemSetTransactionList(data_iterator):
	"""
	从候选集中获取所有子项集
	"""
    transactionList = list()
    itemSet = set()
    for record in data_iterator:
        transaction = frozenset(record)
        transactionList.append(transaction)
        for item in transaction:
            itemSet.add(frozenset([item]))  
    return itemSet, transactionList

参数设置：最小支持度：0.15 最小置信度： 0.6

• 城市名字数据集结果如下：
  
  换一个超市销售数据集：

频繁项集：

• 关联关系挖掘结果

挺好玩的，代码不是很难，但是网上的代码都年久失修，我调了很久，更新一些地方的写法（很暴力的循环，可能增加了复杂度和开销，太菜了能跑起来就是万幸了呜呜呜~）

别忘辽~ 记得给个赞！

---

优化策略

1. 将置信度换成提升度 提升度：$$lift(A->B)=\frac{confidence(A->B)}{p(B)}=\frac{support(BA)}{support(A)\ast P(B)}$$
   但是提升度会收到零事务的影响
2. 不用提升度，不受零事务影响但是会受到不平衡数据的影响
3. 使用哈希树来分组计数
   * 减少支持度的计算开销
   * 项集和计数同时都在叶子节点

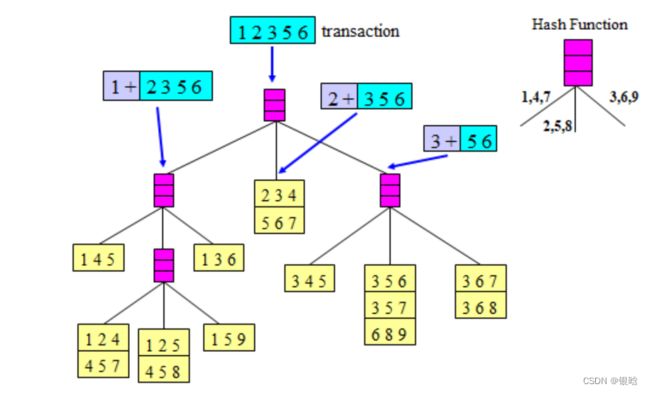
事务：{1,2,3,5,6}

项集：
在Apriori算法中，当查看一个候选集是否是频繁项集，需要将该候选集与DB中的每个事务进行比较，如果该候选集在这个事务中出现了，就将其支持度加1。当DB中有5个事务，而候选项集为3个的时候，其总的比较次数就是3×5=15次

为了减少比较的次数，通过以Hash树的结构来存储候选集，每一个事务不再和每个候选集进行比较，而是和Hash树中特定的候选集进行比较

---

构建哈希树：

1. 设置最大叶子节点数，大于这个阈值就要分裂，这里我们的Max_leaf_size选择为3。
2. 通过取模运算获得哈希位置
3. 分成3个数，最大哈希3次

举例说明：

Step1： 遍历候选集（也就是上面的15个项集）

对于项集{1，4，5}来说，对第一项 1 来说根据hash函数，应该放在左边

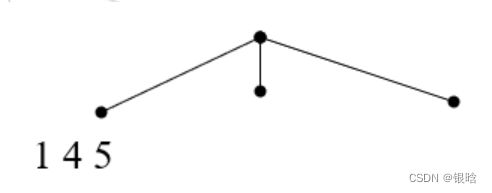
对于项集{1，2，4}来说，其第一项为1，也放在左边。

• 也就是说，第一项取模为1的，都放在根节点的左边

对于项集{4，5，7}来说，第一项为4，放在左边，但这时因为左边有3个候选集，需要进行分裂，这时我们根据候选集的第二项进行hash

注意：如果发现一个叶子节点的数目>=3，如果可以hash进行分类就分裂，如果三个数hash结果都一样，那就放在一起以线性表的结构存起来

• 其余节点依次类推…

Step 2 :

求一个事务可能的子项集，以事务{1，2，3，5，6}为例，求该事务可能存在的三项集。可能的三项集数目应该是$C_5^3$共10个。

• 这一步其实就是对可能的三项集提前进行分桶（为了后面哈希树的快速查找打好基础）
  
• 这样以来，10个可能的三项集变成6个桶了，计算支持度的时候直接去对应hash桶里找，然后比较

使用Hash树进行支持度计数

构建的hash树就长这样

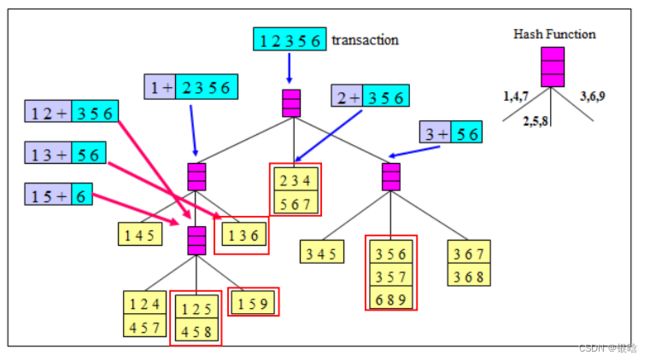
分桶查找

待支持度计数的项集

---

• 对于事务{1，2，3，5，6}，首项为1的项集，应该投递在左边，而首项为2的投递在中间，首项为3的投递在右边

1. 对于前两项为1，2的其可能的项集为{1，2，3}，{1，2，5}，{1，2，6}

• {1，2，3}，{1，2，6}应该投递在右，与{1，5，9}叶子节点中数据进行比较，没有相同的,支持度为0
• {1，2，5}应该投递在中间，与{1，2，5}，{4，5，8}结点进行比较，存在项集{1，2，5}，因此{1，2，5}的支持度计数加1

2. 对于项集前两项为1，3的前提下，因为只有一个叶子节点，因此不需要再对第三项进行投递，因此直接和{1，3，6}叶子节点进行比较，{1，3，6}有相同的，{1，3，6}支持度+1

3. 对于项集前两项为1，5的前提下，只有一个叶子节点{1，5，6}，不需要投递，直接和{1，5，6}比较，不相同，支持度为0

4. 对于项集前两项为{2，3}，{2，5}的前提下，只有两个节点{2，3，4}{5，6，7}，没有相同的，支持度为0

5. 对于项集前两项为3，5的前提下，有三个节点{3，5，6}，{3，5，7}，{6，8，9}，有一个相同的，{3，5，6}支持度+1

• 红框内就是需要比较的项集，红框内一共9个项集，也就是算支持度的时候只有比较9次，而不是逐一遍历的15次

所以，最后得到的频繁项集为{1，2，5}，{3，5，6}，{1，3，6}