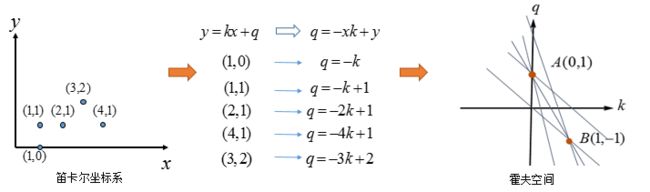【matlab图像处理笔记4】【图像变换】(三)图像的霍夫变换
文章目录
- 推荐阅读
- 前言
- 霍夫变换概述
- 霍夫变换直线检测原理
-
- 从笛卡尔坐标系到霍夫空间
- 两点一线的霍夫空间形式
- 寻找共线的点
- 直角坐标系存在的问题
- 极坐标参数空间下的霍夫变换
- matlab霍夫变换直线检测示例
-
- 检测步骤
- 示例以及代码
-
- 原图
- 边缘检测
- 对二值图像霍夫变换
- 寻找霍夫空间中的交点
- 在笛卡尔坐标系绘制线段
-
- 关于houghlines的补充说明
- 完整代码
推荐阅读
本系列其他文章
- 【matlab图像处理笔记2】【图像变换】(一)图像的算术运算与几何变换、图像插值算法_Twilight Sparkle.的博客-CSDN博客
- 【matlab图像处理笔记3】【图像变换】(二)图像的形态学变换_Twilight Sparkle.的博客-CSDN博客
参考教程/推荐文章
- 霍夫变换 - 疯狂奔跑 - 博客园 (cnblogs.com)
- 【OpenCV入门教程之十四】OpenCV霍夫变换:霍夫线变换,霍夫圆变换合辑_浅墨_毛星云的博客-CSDN博客
- 第16章:霍夫变换_李淳罡Lichungang的博客-CSDN博客_霍夫变换
- 霍夫变换(Hough Transformation)基本思想及MATLAB相关函数_wendy_ya的博客-CSDN博客_hough变换的基本思想
前言
本篇将介绍图像变换中的霍夫变换,该文章不会对霍夫变换做太过于详细的推导,将更注重于霍夫变换的理解与应用。
本篇文章主要介绍霍夫变换直线检测。
霍夫变换概述
霍夫变换是一种在图像中寻找直线、圆形以及其他简单形状的方法,广义上的霍夫变换可以找到你想要的任何你可以描述的特征。
霍夫变换采用类似于投票的方式来获取当前图像内的形状集合,该变换由Paul Hough(霍夫)于1962年首次提出。最初的霍夫变换只能用于检测直线,经过发展后,霍夫变换不仅能够识别直线,还能识别其他简单的图形结构,常见的有圆、椭圆等。实际上,只要是能够用一个参数方程表示的对象,都适合用霍夫变换来检测。
霍夫变换直线检测原理
从笛卡尔坐标系到霍夫空间
直线变为点
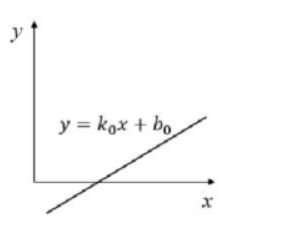
在笛卡尔坐标系中,存在一条直线 y = k 0 x + b 0 y=k_0x+b_0 y=k0x+b0
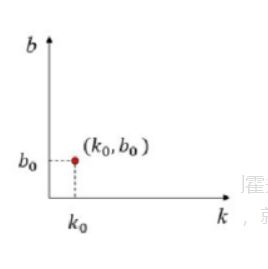
将 y = k 0 x + b 0 y=k_0x+b_0 y=k0x+b0写为关于 ( k , b ) (k,b) (k,b)的函数:
b 0 = − k 0 x + y b_0 = -k_0x+y b0=−k0x+y
变换后的空间称为霍夫空间。此时笛卡尔坐标系中的直线将表示为霍夫空间中的一个点:
同时也可以从霍夫空间逆变换为笛卡尔空间。
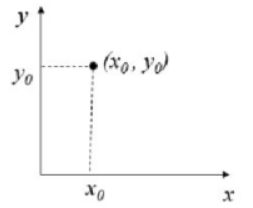
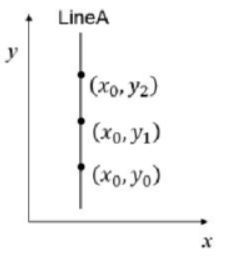
点变为直线
在笛卡尔坐标系中,存在一个点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0),
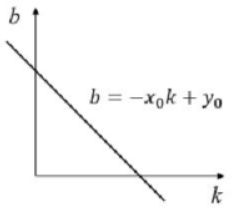
通过该点的直线可表示为: y 0 = k x 0 + b y_0 = kx_0+b y0=kx0+b 。变换后为 b = − k x 0 + y 0 b = -kx_0+y_0 b=−kx0+y0。此时笛卡尔坐标系中的一个点将表示为霍夫空间中的一条直线:
两点一线的霍夫空间形式
现在在笛卡尔坐标系中,有两个点:
我们知道,两点确定一条直线。现在来思考这两个点在霍夫空间将以什么形式表示这条直线。在霍夫空间中,这两个点对应不同的直线。那么在霍夫空间中,这两条直线的交点,就是笛卡尔坐标系中对应的直线。
寻找共线的点
现在我们将点位增多,并开始在这些点中寻找共线的点以及对应的直线。
那么根据霍夫空间交点即笛卡尔空间共线的规则,右图的交点都说明共线。但是右图的交点为什么无视了两个呢?
这是因为霍夫变换后处理的基本方式是:选择由尽可能多直线汇成的点。通常情况下,我们需要设置一个阈值,当霍夫坐标系内交于某点的曲线达到了阈值,就认为在对应的极坐标系内存在(检测到)一条直线。
现在逆变换回笛卡尔坐标系,看看这两个橙色的交点代表的直线:
可以看到我们成功找到了共线的点对应的直线,但此时的霍夫变换还存在问题。
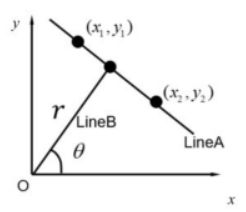
直角坐标系存在的问题
考虑下图的情况,即共线的直线垂直于x轴,此时直线的斜率k为无穷大,截距b无法取值。因此,下图的垂线无法映射至霍夫空间。为了解决该问题,我们需要将直角坐标系换位极坐标系。
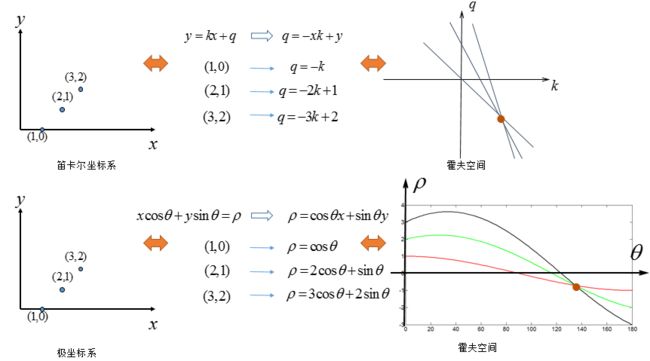
极坐标参数空间下的霍夫变换
在极坐标中的直线可以表示为:
r = x c o s θ + y s i n θ r = xcos\theta+ysin\theta r=xcosθ+ysinθ
现在将极坐标的点映射至霍夫空间,霍夫空间的参数变为 r , θ r,\theta r,θ ,对比图如下:
同样的规则,交点为共线。
matlab霍夫变换直线检测示例
现在使用matlab实现的霍夫变换做一个具体的示例。
检测步骤
-
对原图像进行边缘检测同时二值化。
(关于边缘检测的相关内容将在之后的文章中更新)二值化以后,我们就可以通过找非零点的坐标确定数据点的位置。即将像素图像变成笛卡尔坐标系的坐标集合。
-
对二值化后的图像进行霍夫变换。
-
在霍夫空间中寻找满足条件的交点。
-
在笛卡尔坐标系,将霍夫变换中找到的交点变成直线,再以线段的形式绘制出来。
这一步待会儿会特别说明一下
示例以及代码
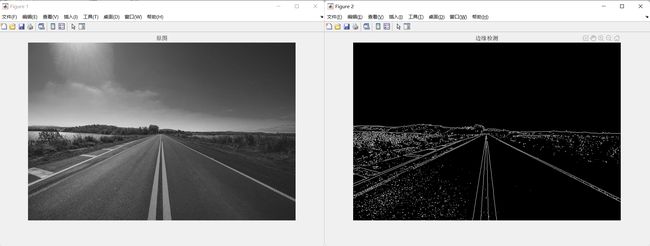
原图
边缘检测
clc;clear;close all;
I = imread('example3.jpg');
I = rgb2gray(I); % 灰度化
figure();imshow(I);title('原图');
BW = edge(I,'prewitt'); % 边缘检测
figure();imshow(BW);title('边缘检测');
对二值图像霍夫变换
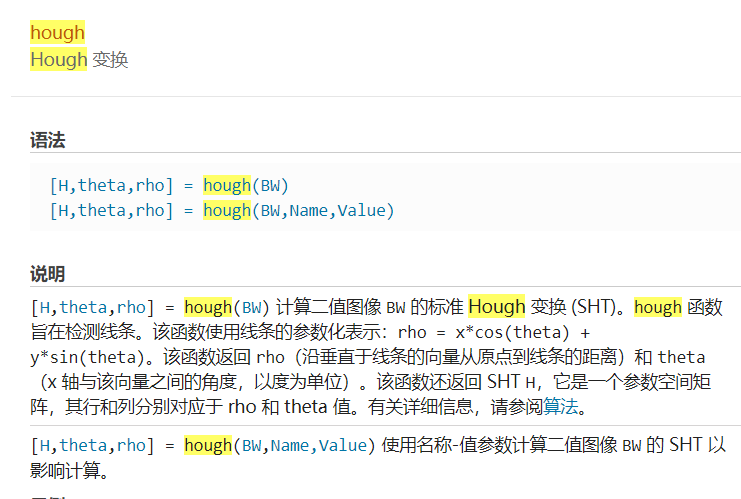
matlab中使用hough函数对二值图像进行霍夫变换。
函数用法:Hough 变换 - MATLAB hough - MathWorks 中国
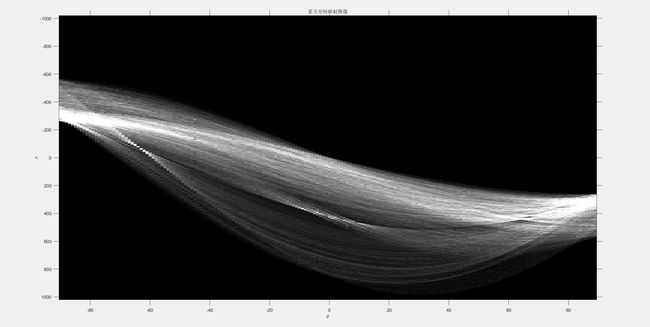
% 霍夫变换
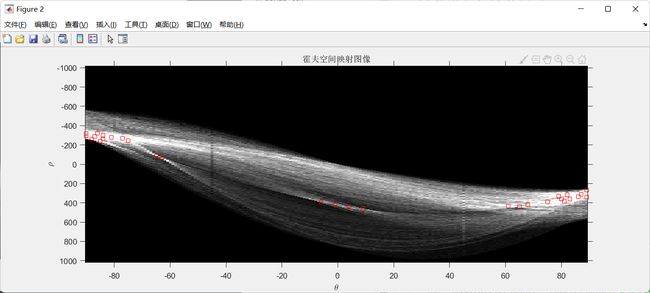
[H,theta,rho] = hough(BW);
figure();imshow(imadjust(mat2gray(H)),[],'XData',theta,'YData',rho,...
'InitialMagnification','fit');
xlabel('\theta');ylabel('\rho');
axis on, axis normal, hold on; % 调整图像比例,不然会很窄
title('霍夫空间映射图像');
边缘检测后的二值图像在霍夫空间上的映射图像:
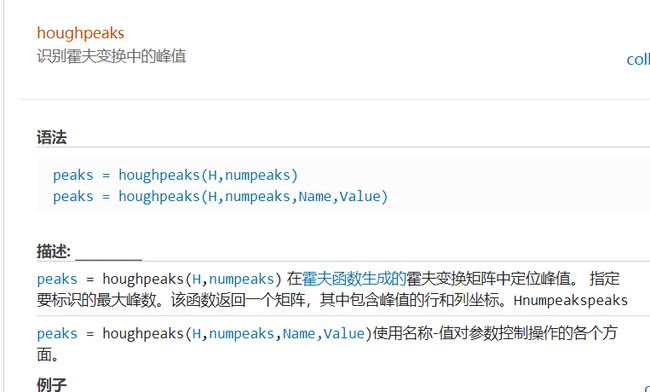
寻找霍夫空间中的交点
matlab中使用houghpeaks函数在霍夫空间寻找满足条件的交点。
函数用法:Identify peaks in Hough transform - MATLAB houghpeaks - MathWorks 中国
% 在Hough矩阵中寻找前30个大于Hough矩阵中最大值0.3的交点(交点即峰值)
P = houghpeaks(H,30,'threshold',ceil(0.3*max(H(:))));
x = theta(P(:,2));y = rho(P(:,1));
plot(x,y,'s','color','red');
在笛卡尔坐标系绘制线段
matlab中使用houghlines函数将在霍夫空间寻找到的交点提取成笛卡尔坐标系的线段(注意不是直线!)
函数用法:基于 Hough 变换提取线段 - MATLAB houghlines - MathWorks 中国
% 在笛卡尔坐标系中找到这些直线
% 合并距离小于20的线段,丢弃所有长度小于2的线段
lines=houghlines(BW,theta,rho,P,'FillGap',20,'Minlength',2);
figure();imshow(BW);hold on;
max_len = 0;
for k = 1:length(lines) % 依次标出各条直线段
xy = [lines(k).point1; lines(k).point2];
plot(xy(:,1),xy(:,2),'LineWidth',2,'Color','blue');
% 绘制线段的起点和终点
plot(xy(1,1),xy(1,2),'x','LineWidth',2,'Color','yellow');
plot(xy(2,1),xy(2,2),'x','LineWidth',2,'Color','red');
% 确定最长线段的端点
len = norm(lines(k).point1 - lines(k).point2);% 最长线段的长度
if ( len > max_len)
max_len = len;
xy_long = xy;
end
end
关于houghlines的补充说明
我最开始没搞清啊,就觉得很奇怪:找到的线明显比交点多啊,这是为什么?
然后仔细研究才发现它是把直线拆成了很多根线段,现在我们只找一个交点就很容易看清楚了:
可能图有点小,但是很明显可以看到它把一条直线拆成了两个线段。
完整代码
clc;clear;close all;
I = imread('example3.jpg');
figure();imshow(I);title('原图');
I = rgb2gray(I); % 灰度化
BW = edge(I,'Prewitt'); % 边缘检测
figure();imshow(BW);title('边缘检测');
% 霍夫变换
[H,theta,rho] = hough(BW);
figure();imshow(imadjust(mat2gray(H)),[],'XData',theta,'YData',rho,...
'InitialMagnification','fit');
xlabel('\theta');ylabel('\rho');
axis on, axis normal, hold on; % 调整图像比例,不然会很窄
title('霍夫空间映射图像');
% 在Hough矩阵中寻找前30个大于Hough矩阵中最大值0.5峰值
P = houghpeaks(H,30,'threshold',ceil(0.3*max(H(:))));
x = theta(P(:,2));y = rho(P(:,1));
plot(x,y,'s','color','red');
% 在笛卡尔坐标系中找到这些直线
% 合并距离小于20的线段,丢弃所有长度小于2的线段
lines=houghlines(BW,theta,rho,P,'FillGap',20,'Minlength',2);
figure();imshow(BW);hold on;
max_len = 0;
for k = 1:length(lines) % 依次标出各条直线段
xy = [lines(k).point1; lines(k).point2];
plot(xy(:,1),xy(:,2),'LineWidth',2,'Color','blue');
% 绘制线段的起点和终点
plot(xy(1,1),xy(1,2),'x','LineWidth',2,'Color','yellow');
plot(xy(2,1),xy(2,2),'x','LineWidth',2,'Color','red');
% 确定最长线段的端点
len = norm(lines(k).point1 - lines(k).point2);% 最长线段的长度
if ( len > max_len)
max_len = len;
xy_long = xy;
end
end
来个成果集合图:
到这里霍夫变换直线检测就写完了。但是霍夫变换的应用明显不止这么点,我原本想把圆环检测也写了,奈何时间确实不够,感兴趣的话就只能自行拓展啦。
写完本文已经是晚上1点了,明早还有早课,准备早课补眠喽~