VAE 实验报告
VAE 实验报告
- 1. 任务定义
- 2. 实验环境
- 3. 方法描述
-
- 3.1 VAE.py
-
- 3.1.1 损失函数定义
- 3.1.2 VAE模型实现
- 3.2 train.py
-
- 3.2.1 数据加载
- 3.2.2 模型、优化器与损失函数初始化
- 3.2.3 模型训练与图像绘制
- 4. 结果分析
-
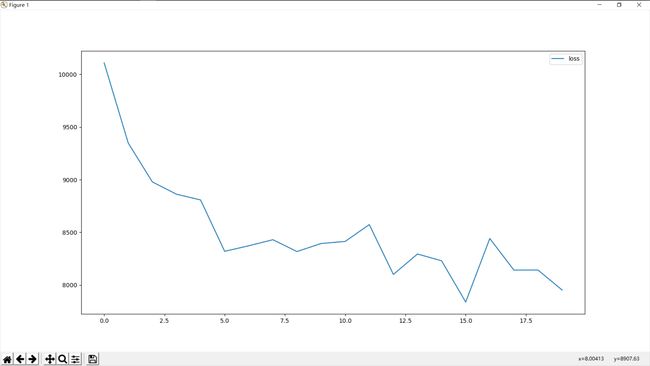
- 4.1 loss变化图像
- 4.2 观察原始图像与生成图像
1. 任务定义
本题目尝试用 VAE 生成 MNIST 风格的手写数字。与 AE 不同，VAE 试图从特定分布中采样出一个隐变量，交由解码器学习一个与观测数据相同的分布。然后从学习得到的分布中采样得到新数据。采用 MNIST 数据训练一个 VAE 模型（卷积网络或多层感知机网络），并使用学习好的 VAE 模型，生成与训练数据相似的新图像，并将其打印出来。
- 注意：可以使用最小均方误差作为模型的损失，记录和观察训练过程中损失函数的变化，以判断模型过拟合或欠拟合情况。
- 注意：反向传播不能通过一个随机采样过程进行，所以从均值和方差中采样得到隐变量后，需要用到重参数技巧(reparameterization trick)。
2. 实验环境
- Windows 10
- VS Code
- python 3.7.8
- torch 1.9.0+cu102
3. 方法描述
- 按文件说明
3.1 VAE.py
- VAE模型实现部分
3.1.1 损失函数定义
- VAE的损失函数由两部分的和组成（bce_loss、kld_loss)。bce_loss即为binary_cross_entropy（二分类交叉熵）损失，即用于衡量原图与生成图片的像素误差。kld_loss即为KL-divergence（KL散度），用来衡量潜在变量的分布和单位高斯分布的差异。
损失函数实现
def loss_func(recon_x, x, mu, logvar):
BCE_loss = nn.BCELoss(reduction='sum')
recon_loss = BCE_loss(recon_x, x)
KLD = -0.5 * torch.sum(1 + logvar - mu**2 - logvar.exp())
return recon_loss + KLD
3.1.2 VAE模型实现
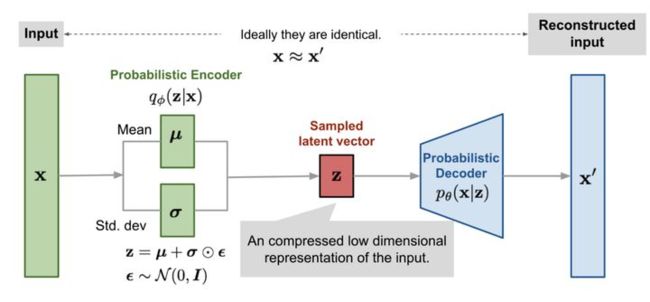
- VAE的结构由两个部分的网络所构成：
-
编码器部分能够学习到根据输入样本X来形成一个特定分布，从中我们可以对一个隐藏变量进行采样，而这个隐藏变量极有可能生成X里面的样本。为了使得Q(z|X)服从高斯分布，这部分需要被优化。
-
解码器部分能够学习到根据给定的一个隐藏变量z作为输入，生成一个具有真实数据分布的输出。该部分将经过采样后的z(最初来自正态分布)映射到一个更复杂的隐藏空间去(实际数据的空间)，并通过这个复杂的隐藏变量z生成一个个的数据点，这些数据点十分接近真实数据的分布。
VAE工作流程图
实现代码
class VAE(nn.Module):
def __init__(self):
super(VAE, self).__init__()
self.fc1 = nn.Linear(28 * 28, 400)
self.fc2_mean = nn.Linear(400, 20)
self.fc2_logvar = nn.Linear(400, 20)
self.fc3 = nn.Linear(20, 400)
self.fc4 = nn.Linear(400, 28 * 28)
self.relu = nn.ReLU()
self.sigmoid = nn.Sigmoid()
def encode(self, x):
h1 = self.relu(self.fc1(x))
return self.fc2_mean(h1), self.fc2_logvar(h1)
def reparamertrize(self, mu, logvar):
std = torch.exp(logvar / 2)
eps = torch.rand_like(std)
return eps * std + mu
def decode(self, z):
h3 = self.relu(self.fc3(z))
return self.sigmoid(self.fc4(h3))
def forward(self, x):
mu, logvar = self.encode(x)
z = self.reparamertrize(mu, logvar)
return mu, logvar, self.decode(z)
3.2 train.py
3.2.1 数据加载
- 采用MNIST数据集
BATCH_SIZE = 128
train_data = datasets.MNIST(
root='./dataset/',
train=True,
transform=transforms.ToTensor(),
download=True
)
train_loader = DataLoader(
dataset=train_data,
batch_size=BATCH_SIZE,
shuffle=True
)
3.2.2 模型、优化器与损失函数初始化
device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
LR = 1e-3
model = VAE().to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=LR)
pca = decomposition.PCA()
3.2.3 模型训练与图像绘制
# 记录loss变化
loss_list = []
for epoch in trange(EPOCH):
epoch_iterator = tqdm(train_loader, desc="Iteration")
for step, batch in enumerate(epoch_iterator):
# 由于是无监督模型，只采用data部分
data, targets = batch
real_imgs = data.view(-1, 28 * 28).to(device)
mu, logvar, gen_imgs = model(real_imgs)
loss = loss_func(gen_imgs, real_imgs, mu, logvar)
optimizer.zero_grad()
loss.backward()
optimizer.step()
print('Epoch {}, loss: {}'.format(epoch, loss))
loss_list.append(loss)
# 将原始图像与生成图像拼接绘制，左侧为原始图像，右侧为生成图像
concat_imgs = torch.cat([real_imgs.view(-1, 1, 28, 28),
gen_imgs.view(-1, 1, 28, 28)], dim=3)
save_image(concat_imgs, 'images/concat_image-{}.png'.format(epoch))
plt.plot(range(len(loss_list)), loss_list, label='loss')
plt.legend()
plt.show()
- 通过 PCA 将学习到的隐变量的均值和方差，映射到二维平面，绘制隐变量的概率密度函数
with torch.no_grad():
mu_re = pca.fit_transform(mu.cpu().numpy())[0, 0]
logvar_re = pca.fit_transform(logvar.cpu().numpy())[0, 0]
x = np.linspace(mu_re - 6 * logvar_re, mu_re + 6 * mu_re, 100)
y = normal_distribution(x, mu_re, logvar_re)
plt.plot(x, y, color='b')
plt.show()
4. 结果分析
4.1 loss变化图像
- 在第6个epoch之前loss快速下降，之后开始振荡。
4.2 观察原始图像与生成图像
-
可以看到，除个别数字不够清晰之外基本与原始图像一致
-
减少隐变量的均值和方差至10维，图像较20维时更模糊
-
增加隐变量的均值和方差至30维，图像变得更加清晰，基本均与原图像一致
-
不难得出结论，隐变量的均值和方差的维度对生成结果的清晰度有显著影响，更多维度的均值和方差有助于结果的生成。