机器学习-变分自编码器VAE实战(三)
本篇主要内容是变分自编码器VAE的实战,希望大家可以对比机器学习-自编码器AE实战(二)
进行对照学习,尤其是在自定义VAE类,以及网络训练部分,会有较大的不同。本人一般都在线,有问题或者建议随时留言,看到了就会回复。
目录
1.数据集加载:
2.自定义VAE类:
定义网络层:
编码器具体实现:
重参数(Reparameterization Trick)的应用:
解码器:
前向传播:
3.网络训练:
4.生成图片:
1.数据集加载:
h_dim = 20
batchsz = 512
lr = 1e-3
(x_train, y_train), (x_test, y_test) = keras.datasets.fashion_mnist.load_data()
x_train, x_test = x_train.astype(np.float32) / 255., x_test.astype(np.float32) / 255.
# we do not need label
train_db = tf.data.Dataset.from_tensor_slices(x_train)
train_db = train_db.shuffle(batchsz * 5).batch(batchsz)
test_db = tf.data.Dataset.from_tensor_slices(x_test)
test_db = test_db.batch(batchsz)
print(x_train.shape, y_train.shape)
print(x_test.shape, y_test.shape)
z_dim = 10本次数据集选用的是Fashion Mnist,和Mnist相比略显复杂,也是黑白图片。
注意,自编码器不需要标签信息,仅规格化数据信息,构建训练集和测试集时也不需要标签信息。
几个预设参数:
h_dim;经过编码降到的维度数
batchsz 和lr 大家应该比较熟悉了,代表分批大小和学习率
注意相对于AE,此处多了一个z_dim:它表示生成方差和均值向量的长度
2.自定义VAE类:
定义网络层:
class VAE(keras.Model):
def __init__(self):
super(VAE, self).__init__()
# Encoder
self.fc1 = layers.Dense(128)
self.fc2 = layers.Dense(z_dim) # get mean prediction
self.fc3 = layers.Dense(z_dim)
# Decoder
self.fc4 = layers.Dense(128)
self.fc5 = layers.Dense(784)此处构建编码器和解码器,解码器和AE是没差别的,都是将z一步一步重构为初始维度;但编码器存在差别fc2和fc3分别对应均值和方差。注意看,都没加激活函数。
编码器具体实现:
def encoder(self, x):
h = tf.nn.relu(self.fc1(x))
# get mean
mu = self.fc2(h)
# get variance
log_var = self.fc3(h)
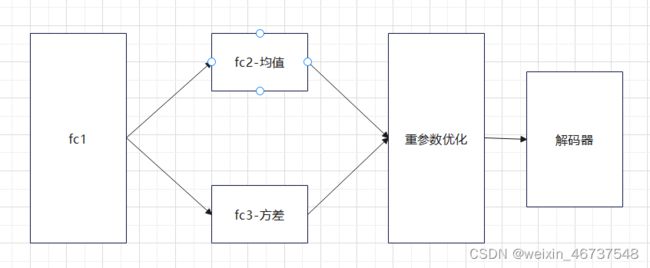
return mu, log_var经过上面的介绍大家也能看出VAE的编码器和AE的区别,其中fc1作为共享层, 直接给输入,并使用relu激活函数得到第一层的输出。下面就和我们以往接触的全连接层有所不同,它并不是一条路到底,而是在此处有了分叉,同一个输入分别进入不同的全连接层,得到不同的结果,一个是均值,一个是方差,最后返回这两个结果。
重参数(Reparameterization Trick)的应用:
重参数相关只是可以看我前面的文章
机器学习-自编码器,变分自编码器及其变种的基本原理(一)
def reparameterize(self, mu, log_var):
eps = tf.random.normal(log_var.shape)
std = tf.exp(log_var*0.5)
z = mu + std * eps
return z大家此处只需要知道z=均值+标准差*eps。eps是从标准正态分布中采样得到的,并且形状和标准差以及方差一样。
咱们来看代码:eps随机采样自正态分布,正态分布的参数只指定了形状为方差的形状,其他均为默认,则是均值为0,方差为1的标准正态分布。接着std标准差就是方差开根号即可。
最终经过重参数优化得到可以进入解码器的z。
解码器:
def decoder(self, z):
out = tf.nn.relu(self.fc4(z))
out = self.fc5(out)
return out解码器就比较中规中矩了,和AE差不多,有不懂的可以留言。
前向传播:
def call(self, inputs, training=None):
# [b, 784] => [b, z_dim], [b, z_dim]
mu, log_var = self.encoder(inputs)
# reparameterization trick
z = self.reparameterize(mu, log_var)
x_hat = self.decoder(z)
return x_hat, mu, log_var流程大概就是这么个流程
3.网络训练:
model = VAE()
model.build(input_shape=(4, 784))
optimizer = tf.optimizers.Adam(lr)
for epoch in range(1000):
for step, x in enumerate(train_db):
x = tf.reshape(x, [-1, 784])
with tf.GradientTape() as tape:
x_rec_logits, mu, log_var = model(x)
rec_loss = tf.nn.sigmoid_cross_entropy_with_logits(labels=x, logits=x_rec_logits)
rec_loss = tf.reduce_sum(rec_loss) / x.shape[0]
kl_div = -0.5 * (log_var + 1 - mu**2 - tf.exp(log_var))
kl_div = tf.reduce_sum(kl_div) / x.shape[0]
loss = rec_loss + 1. * kl_div
grads = tape.gradient(loss, model.trainable_variables)
optimizer.apply_gradients(zip(grads, model.trainable_variables))
if step % 100 == 0:
print(epoch, step, 'kl div:', float(kl_div), 'rec loss:', float(rec_loss))设定网络对象为AE()。规定输入规格。规定使用Adam优化器,并指定学习率。
循环1000轮,将图片打平,构建梯度下降记录器。
经过网络,得到三个参数分别是:重构后的x即x_rec_logits,均值,方差。
我们前面讲过变分自编码器的损失函数有两部分。即重建损失和KL散度组成。
重建损失:即利用激活函数为sigmoid的交叉熵求损失函数,两个参数分别为原始输入和重构后的输入。对损失函数求和之后除以分批的个数,得到每一张图片的重构损失的平均值。
KL散度:当其中一个正态分布符合 (mu,log_var ),另一个是标准正态分布是,实际上是固定公式直接代入计算得到KL散度,再求和计算平局值即可。
最后将重建损失和KL散度求和即得出真正的损失函数
进行自动求导与自动更新即可。
4.生成图片:
z = tf.random.normal((batchsz, z_dim))
logits = model.decoder(z)
x_hat = tf.sigmoid(logits)
x_hat = tf.reshape(x_hat, [-1, 28, 28]).numpy() *255.
x_hat = x_hat.astype(np.uint8)
save_images(x_hat, 'D:\桌面\文档\结果\结果果sampled_epoch%d.png'%epoch)
x = next(iter(test_db))
x = tf.reshape(x, [-1, 784])
x_hat_logits, _, _ = model(x)
x_hat = tf.sigmoid(x_hat_logits)
x_hat = tf.reshape(x_hat, [-1, 28, 28]).numpy() *255.
x_hat = x_hat.astype(np.uint8)
save_images(x_hat, 'D:\桌面\文档\结果\结果果rec_epoch%d.png'%epoch)给了两种图片生成方式,并可以进行可视化对比:
上面这一种是直接生成图片方式,直接从先验分布中获取z,并利用解码器生成图片
下面这一种是利用编码器和解码器,以及重参数等方式最终得出重建后的图片
经过对比,重建的效果更好。
代码来自于《TensorFlow深度学习》-龙龙老师
![]()