《PyTorch深度学习实践》完结合集--B站刘二大人学习总结

本篇主要是各类模型的基本介绍及应用，不涉及深层技术。

学习视频指路→B站指路

代码实践指路→代码指路

课件获取：通过百度网盘分享的文件：PyTorch深…
链接:https://pan.baidu.com/s/1iSY7LgEigOWUWEBLmN1j0A?pwd=ect0 
提取码:ect0
复制这段内容打开「百度网盘APP 即可获取」

目录

正文开始：

1.Overview

2.线性模型

3.梯度下降算法

4.反向传播

5.用PyTorch实现线性回归

6.逻辑斯蒂回归

7.处理多维特征的输入

8.加载数据集

9.多分类问题

10.卷积神经网络（基础篇）

11.卷积神经网络（高级篇）

12.循环神经网络（基础篇）

13.循环神经网络（高级篇）

---

正文开始：

1.Overview

        第一讲比较浅显只讲部分

Figure.1 学习系统发展

 学习系统的发展：

1.基于规则的系统：输入→手动设计程序→输出

        设计程序时需要人工制定规则，就要专业背景知识，但是容易遗漏规则，导致系统性能不佳。

2.经典机器学习系统：输入→手动提取特征（张量）→映射函数y=f(x)→输出

3.表示学习：

        输入→提取特征（张量）→映射函数y=f(x)→输出

        深度学习：输入→简单特征→额外层提取特征→映射函数y=f(x)（多层神经网络）→输出

 Figure.2 sk-learn官方算法路径

路径关键点：样本量？分类问题？预测量级？等

2.线性模型

        一般模型训练过程：1.准备数据集。2.选择适合模型。3.根据测试数据训练模型。4.推理及运用。

        我们的数据集一般分两部分，用于训练的训练数据和用于预测的测试数据。但是我们怎么评估这个模型是否可以达到评估标准，我们可以再将训练集分成普通训练集和开发集（用来评估模型）。

 看下图，是一个线性模型的例子：

         上图中，红色的线是我们的真实无差别的模型（现实不容易存在这么简单的模型），两条蓝色的线是我们随机random出来的模型结果，我们需要将random出来的线性模型和真实数据做对比，看他们之间的差异，当然差异越小，我们的模型越准确。那怎么计算差异呢？

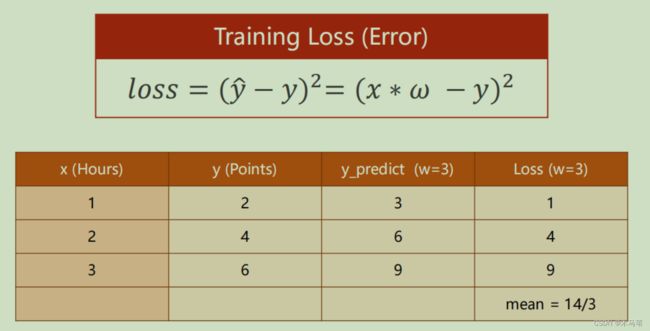
·        我们引入一个Loss损失的概念，损失函数我们常用的是预测结果和真实结果做差，但也有其他算法，所以写论文的时候一定要定义清楚你的Loss函数。

         注意：上图中y hat就是我们随机定义模型的预测结果。这里的Loss取平方主要是为了结果取正值。

         由Loss我们引出一个MSE（平均平方误差）的概念，由上图可以看出，他是一组参数模型或者说是一个随机模型的误差平均值。用MSE就可以选出损失最小的模型。

线性模型例子：

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

#这里设函数为y=3x+2
x_data = [1.0,2.0,3.0]
y_data = [5.0,8.0,11.0]

def forward(x):
    return x * w + b

def loss(x,y):
    y_pred = forward(x)
    return (y_pred-y)*(y_pred-y)

mse_list = []
W=np.arange(0.0,4.1,0.1)
B=np.arange(0.0,4.1,0.1)
[w,b]=np.meshgrid(W,B)

l_sum = 0
for x_val, y_val in zip(x_data, y_data):
    y_pred_val = forward(x_val)
    print(y_pred_val)
    loss_val = loss(x_val, y_val)
    l_sum += loss_val

fig = plt.figure()
ax = Axes3D(fig)
ax.plot_surface(w, b, l_sum/3)
plt.show()

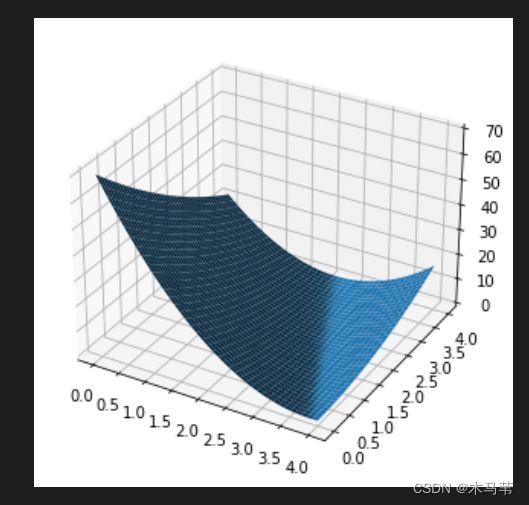
输出结果：

 

 

3.梯度下降算法

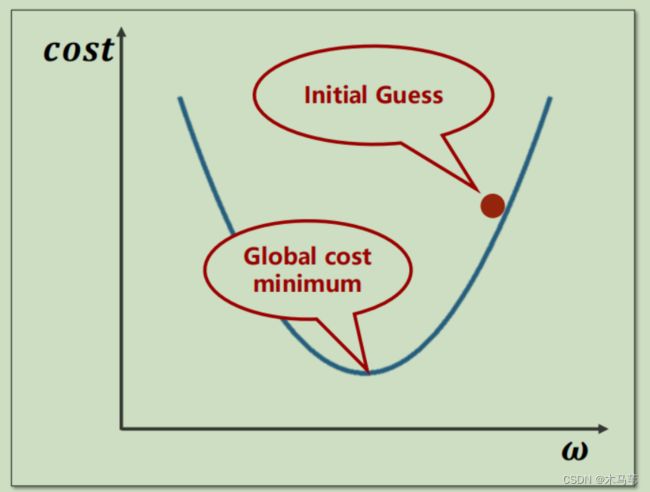
在我们构建模型时，需要找到损失函数最小的点来确定最佳模型，如何确定最小损失值，见下图。

Figure3.1 

通过不断更新权值w，来选取最小损失。

那么为什么需要采用梯度下降算法，先解释什么是梯度，梯度可以说是求导值/斜率等，当我们知道这个cost与w的变化趋势（斜率）时，你就知道我们w应该往何处变化。比如下图，当他的梯度大于0，说明此处是增函数，趋势上升，w越大，cost越大，所以我们应该降低w。

        Figure3.2

 GD梯度下降算法：

import matplotlib.pyplot as plt
 
# prepare the training set
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
 
# initial guess of weight 
w = 1.0
 
# define the model linear model y = w*x
def forward(x):
    return x*w
 
#define the cost function MSE 
def cost(xs, ys):
    cost = 0
    for x, y in zip(xs,ys):
        y_pred = forward(x)
        cost += (y_pred - y)**2
    return cost / len(xs)
 
# define the gradient function  gd
def gradient(xs,ys):
    grad = 0
    for x, y in zip(xs,ys):
        grad += 2*x*(x*w - y)
    return grad / len(xs)
 
epoch_list = []
cost_list = []
print('predict (before training)', 4, forward(4))
for epoch in range(100):
    cost_val = cost(x_data, y_data)
    grad_val = gradient(x_data, y_data)
    w-= 0.01 * grad_val  # 0.01 learning rate
    print('epoch:', epoch, 'w=', w, 'loss=', cost_val)
    epoch_list.append(epoch)
    cost_list.append(cost_val)
 
print('predict (after training)', 4, forward(4))
plt.plot(epoch_list,cost_list)
plt.ylabel('cost')
plt.xlabel('epoch')
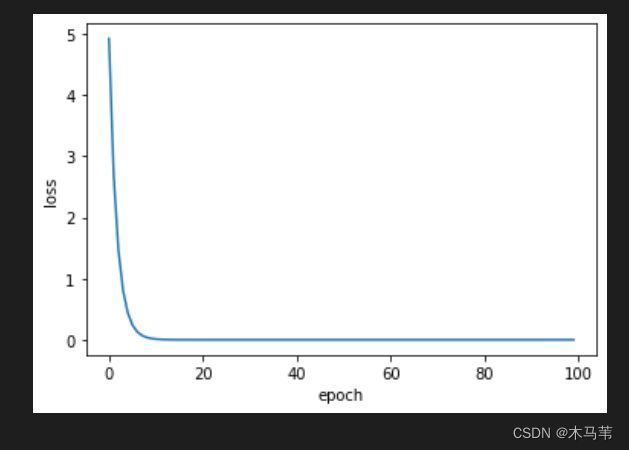
plt.show() 

结果：

        事实情况是，我们很少遇到图3.2这样平滑的损失函数，我们的真实损失函数很可能是坑坑洼洼的，在局部他是一个最低点，但是全局却不是最低点。所以我们一般采用随机梯度下降（SGD）。

 这样选取的就不是连续的平均值而是随机的一组损失值，避免入坑出不来。和梯度下降不同的就只有上图的更新权重和偏导不同，其他都一致。

SGD：

import matplotlib.pyplot as plt
 
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
 
w = 1.0
 
def forward(x):
    return x*w
 
# calculate loss function
def loss(x, y):
    y_pred = forward(x)
    return (y_pred - y)**2
 
# define the gradient function  sgd
def gradient(x, y):
    return 2*x*(x*w - y)
 
epoch_list = []
loss_list = []
print('predict (before training)', 4, forward(4))
for epoch in range(100):
    for x,y in zip(x_data, y_data):
        grad = gradient(x,y)
        w = w - 0.01*grad    # update weight by every grad of sample of training set
        print("\tgrad:", x, y,grad)
        l = loss(x,y)
    print("progress:",epoch,"w=",w,"loss=",l)
    epoch_list.append(epoch)
    loss_list.append(l)
 
print('predict (after training)', 4, forward(4))
plt.plot(epoch_list,loss_list)
plt.ylabel('loss')
plt.xlabel('epoch')
plt.show() 

结果：

 发现更新（训练）的更快。

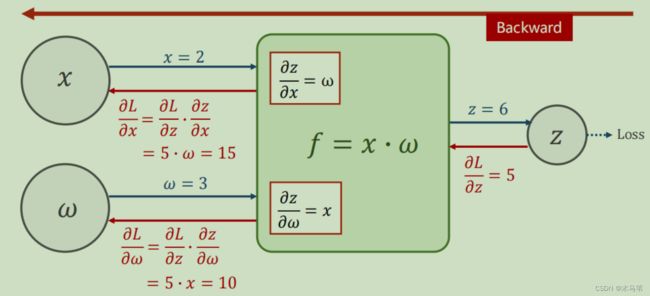
4.反向传播

        这一讲我觉得是可以和上一讲梯度下降合并来讲，什么是反向传播？上图中红色箭头就是反向传播的，其实就是个求偏导的过程，根据反向正负来更新新一轮的权值的过程。

         这里插一句，什么情况下才代表你的模型训练的差不多了，就是函数收敛，不会有大变化的时候，模型就训练完毕，如果继续下去就容易过拟合，导致真实预测不准。

        此处代码就不贴了，如果需要可点这里

5.用PyTorch实现线性回归

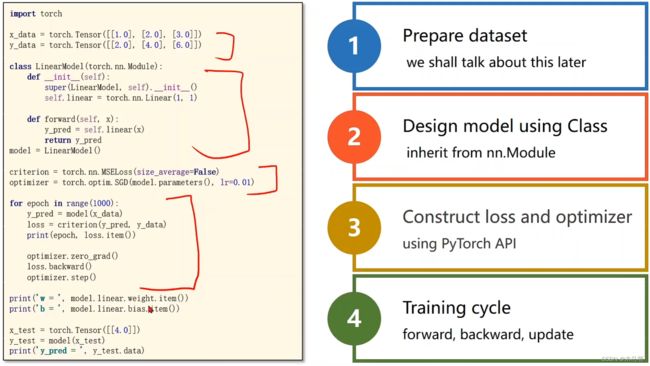
 正题来了，利用PyTorch来写模型。过程见上图。代码对应见下图。

 这一讲和第二讲的线性模型基本没差，只不过把求损失和优化直接调用PyTorch包中方法，十分简便。PS：1.一般定义模型时，我们需要定义一个类，后续如果要使用就直接实例化。2.在反向传播之前一定要手动梯度清零。

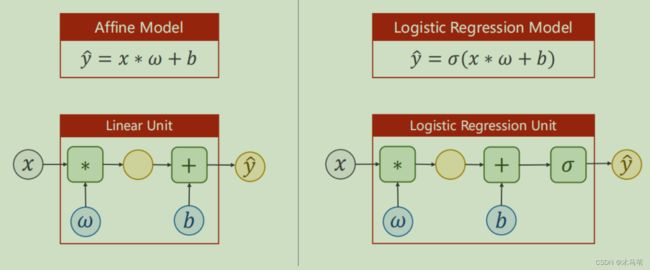
6.逻辑斯蒂回归

分类问题讨论的是该输入属于某个类别的概率是多少。

         逻辑斯蒂回归我们采用了sigmoid（用符号来表示）算法，具体算法见下。

 将w*x+b替换上式中的x。

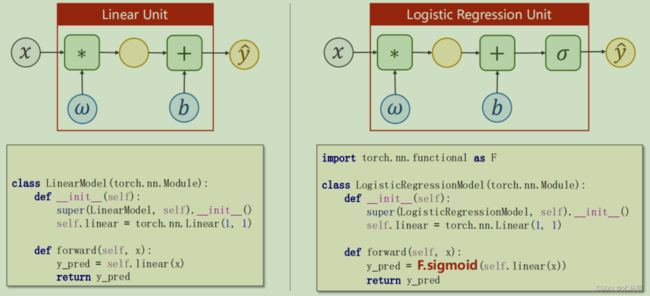
 代码变化见下图：仅多了一个sigmoid调用。

 逻辑斯蒂回归有一个特点，就是他通过sigmoid算法，最后求出的结果只会在0-1之间。

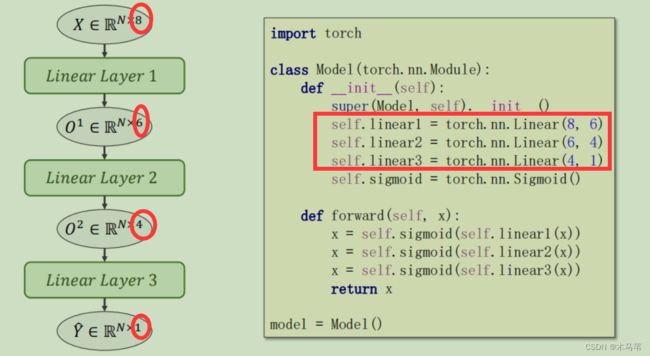
7.处理多维特征的输入

        我们前面几讲的例子在降维处理上只有一层变换，都是输入1维输出1维。但如果我们对数据有多维处理，之前做法就不恰当。

 由上图可以看出，现在需要将8维输入变成1维输出，中间经过了三层线性变换，代码和之前比也只需要多加两个线性模型。其余处理不变。

8.加载数据集

9.多分类问题

10.卷积神经网络（基础篇）

11.卷积神经网络（高级篇）

12.循环神经网络（基础篇）

13.循环神经网络（高级篇）