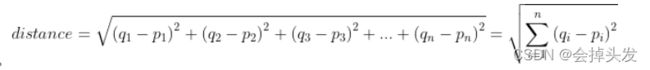KNN实现海伦约会预测
前期准备工作
接上一个文章,我们讲一讲怎么样完成一个数据导入到算法预测的小型实验。
这里我们需要的数据集为海伦约会的数据集,数据集为一个text文件,因为github访问速度的问题,我将数据集上传到百度网盘供大家下载。
点击这里下载
提取码为:wspl
前期的准备工作已经完成,我们开始实现。(不知道算法原理的请看本专题的这篇文章)
一、数据导入
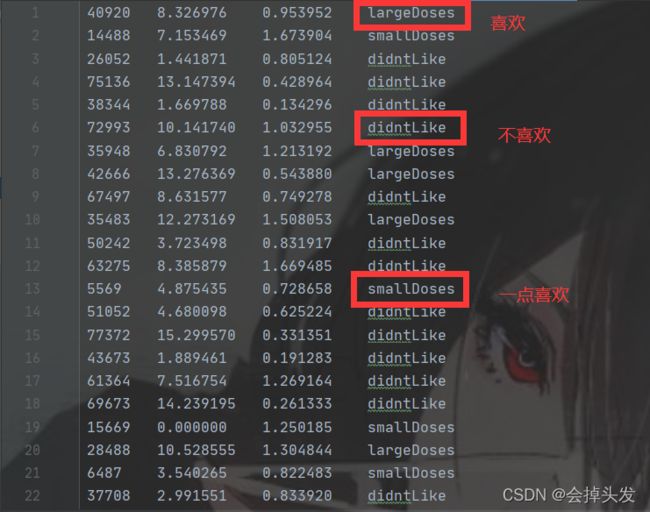
直接打开text文件,我们发现文件里面有四列,前三列为数据的特征,最后一列为标签。他们之前用一个制表符隔开。
我们读取文件的每一行,用split()方法将特征数据提取,并且制作相对应的标签列表,数据与标签之前一一对应,结果返回一个列表和一个矩阵。代码实现和代码讲解如下:
import numpy as np
import operator
import matplotlib.pyplot as plt
import matplotlib.lines as mlines
from matplotlib.font_manager import FontProperties
# 读取数据集
def file2matrix(filename):
# 打开文件
fr = open(filename)
# 读取txt文件的每一行,将每一行作为字符串存入arrayOlines这个列表内
arrayOlines = fr.readlines()
# 通过len()函数获取arrayOlines列表的长度
numberOfLines = len(arrayOlines)
# 通过numpy的zeros()函数创建一个有arrayOlines一样长并且有三列的零矩阵
# zeros((a,b))里面的参数为一个元组的时候表示创建一个a行b列的零矩阵
returnMat = np.zeros((numberOfLines, 3))
# 先声明一个空列表用于存放标签
classLabelVector = []
index = 0
for line in arrayOlines:
# 遍历arrayOlines列表,消除列表中的回车符
line = line.strip()
# 以'\t'作为分隔符,将arrayOlines列表的每个元素分隔开成为一个列表
listFormLine = line.split('\t')
# 并且将返回回来的列表的前三个元素作为returnMat矩阵的行
returnMat[index, :] = listFormLine[0:3]
if listFormLine[-1] == 'didntLike':
classLabelVector.append(1)
elif listFormLine[-1] == 'smallDoses':
classLabelVector.append(2)
elif listFormLine[-1] == 'largeDoses':
classLabelVector.append(3)
# # 创建一个新的字典labels
# labels = {'didntLike': 1, 'smallDoses': 2, 'largeDoses': 3}
# # 以labels字典作为参考,将listFormLine列表的最后一个元素,将这个字符串在字典中对应的键值使用追加的方法依次存入classLabelVector列表中
# classLabelVector.append(labels[listFormLine[-1]])
index += 1
return returnMat, classLabelVector二、分析数据
我们知道,使用KNN算法再对新的数据进行分类的时候,我们采取的标准是计算距离,通过计算新的数据点到其他所有点的距离,使用的也是欧几里得距离计算公式,这里就有出现一个问题,当某一个特征的数据很大的时候,其他的数据特征的影响会变得很小甚至可以忽略不计。用数学表达式可以看出当这个计算距离的公式中
的某一个q和p的值很大的时候,其他的特征影响会减小。这就需要我们将所有的数据特征的值都按比例缩小到一个等级,当然只是对于当前情景适合,因为凯伦约会的这个,她认为这三个特征同等重要,如果遇到其他情景,我们同样可以等比例缩放数据特征从而达到控制特征所占权重,这里我们要达到将他们都缩放到同一级别所要采取的方法就为数据的归一化。
数据的归一化的数学计算方法为:![]()
我们通过这个方法将每个特征的数据都缩放到0~1之间。这就叫做数据的归一化。
具体的代码实现如下:
# 数据的归一化
def autoNorm(dataSet):
# 获得数据的最小值
minVals = dataSet.min(0)
maxVals = dataSet.max(0)
# 最大值和最小值的范围
ranges = maxVals - minVals
# shape(dataSet)返回dataSet的矩阵行列数
normDataSet = np.zeros(np.shape(dataSet))
# 返回dataSet的行数
m = dataSet.shape[0]
# 原始值减去最小值
normDataSet = dataSet - np.tile(minVals, (m, 1))
# 除以最大和最小值的差,得到归一化数据
normDataSet = normDataSet / np.tile(ranges, (m, 1))
# 返回归一化数据结果,数据范围,最小值
return normDataSet, ranges, minVals三、数据的可视化
这里我们还插讲一个数据的可视化,我们通过matplotlib的pyplot库的方法实现数据的可视化。
具体的代码实现如下:
def showdatas(datingDataMat, datingLabels):
# 设置汉字格式
font = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=14)
# 将fig画布分隔成1行1列,不共享x轴和y轴,fig画布的大小为(13,8)
# 当nrow=2,nclos=2时,代表fig画布被分为四个区域,axs[0][0]表示第一行第一个区域
fig, axs = plt.subplots(nrows=2, ncols=2, sharex=False, sharey=False, figsize=(13, 8))
numberOfLabels = len(datingLabels)
LabelsColors = []
for i in datingLabels:
if i == 1:
LabelsColors.append('black')
if i == 2:
LabelsColors.append('orange')
if i == 3:
LabelsColors.append('red')
# 画出散点图,以datingDataMat矩阵的第一(飞行常客例程)、第二列(玩游戏)数据画散点数据,散点大小为15,透明度为0.5
axs[0][0].scatter(x=datingDataMat[:, 0], y=datingDataMat[:, 1], color=LabelsColors, s=15, alpha=.5)
# 设置标题,x轴label,y轴label
axs0_title_text = axs[0][0].set_title(u'每年获得的飞行常客里程数与玩视频游戏所消耗时间占比', FontProperties=font)
axs0_xlabel_text = axs[0][0].set_xlabel(u'每年获得的飞行常客里程数', FontProperties=font)
axs0_ylabel_text = axs[0][0].set_ylabel(u'玩视频游戏所消耗时间占', FontProperties=font)
plt.setp(axs0_title_text, size=9, weight='bold', color='red')
plt.setp(axs0_xlabel_text, size=7, weight='bold', color='black')
plt.setp(axs0_ylabel_text, size=7, weight='bold', color='black')
# 画出散点图,以datingDataMat矩阵的第一(飞行常客例程)、第三列(冰激凌)数据画散点数据,散点大小为15,透明度为0.5
axs[0][1].scatter(x=datingDataMat[:, 0], y=datingDataMat[:, 2], color=LabelsColors, s=15, alpha=.5)
# 设置标题,x轴label,y轴label
axs1_title_text = axs[0][1].set_title(u'每年获得的飞行常客里程数与每周消费的冰激淋公升数', FontProperties=font)
axs1_xlabel_text = axs[0][1].set_xlabel(u'每年获得的飞行常客里程数', FontProperties=font)
axs1_ylabel_text = axs[0][1].set_ylabel(u'每周消费的冰激淋公升数', FontProperties=font)
plt.setp(axs1_title_text, size=9, weight='bold', color='red')
plt.setp(axs1_xlabel_text, size=7, weight='bold', color='black')
plt.setp(axs1_ylabel_text, size=7, weight='bold', color='black')
# 画出散点图,以datingDataMat矩阵的第二(玩游戏)、第三列(冰激凌)数据画散点数据,散点大小为15,透明度为0.5
axs[1][0].scatter(x=datingDataMat[:, 1], y=datingDataMat[:, 2], color=LabelsColors, s=15, alpha=.5)
# 设置标题,x轴label,y轴label
axs2_title_text = axs[1][0].set_title(u'玩视频游戏所消耗时间占比与每周消费的冰激淋公升数', FontProperties=font)
axs2_xlabel_text = axs[1][0].set_xlabel(u'玩视频游戏所消耗时间占比', FontProperties=font)
axs2_ylabel_text = axs[1][0].set_ylabel(u'每周消费的冰激淋公升数', FontProperties=font)
plt.setp(axs2_title_text, size=9, weight='bold', color='red')
plt.setp(axs2_xlabel_text, size=7, weight='bold', color='black')
plt.setp(axs2_ylabel_text, size=7, weight='bold', color='black')
# 设置图例
didntLike = mlines.Line2D([], [], color='black', marker='.',
markersize=6, label='didntLike')
smallDoses = mlines.Line2D([], [], color='orange', marker='.',
markersize=6, label='smallDoses')
largeDoses = mlines.Line2D([], [], color='red', marker='.',
markersize=6, label='largeDoses')
# 添加图例
axs[0][0].legend(handles=[didntLike, smallDoses, largeDoses])
axs[0][1].legend(handles=[didntLike, smallDoses, largeDoses])
axs[1][0].legend(handles=[didntLike, smallDoses, largeDoses])
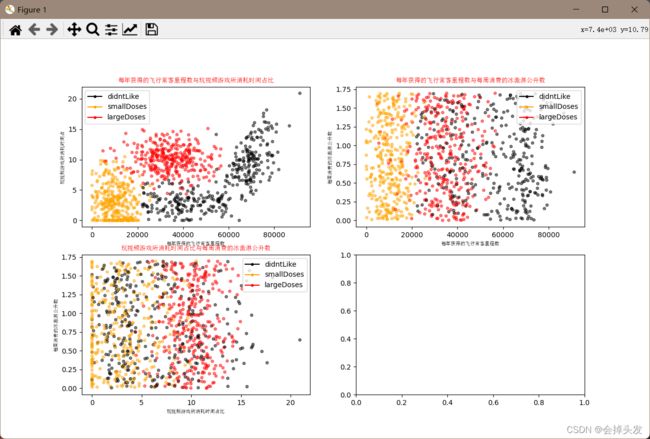
# 显示图片
plt.show()我们显示了三个图像,根据三个特征两两组合,并且根据类别的不同我们采用不同的三种颜色显示数据分布,结果如下:
四、算法预测
算法方面并没有新的改变,仍然使用之前写过的算法形式,只是数据的输入不同而已,具体代码实现如下:
def classify0(inx, dataset, labels, k):
dataSetsize = dataset.shape[0]
diffMat = np.tile(inx, (dataSetsize, 1)) - dataset
sqdiffMat = diffMat ** 2
sqDistances = sqdiffMat.sum(1)
distances = sqDistances ** 0.5
sortedDistIndices = distances.argsort()
classcount = {}
for i in range(k):
voteIlabel = labels[sortedDistIndices[i]]
# print(voteIlabel)
classcount[voteIlabel] = classcount.get(voteIlabel, 0) + 1
sortClassCount = sorted(classcount.items(), key=operator.itemgetter(1), reverse=True)
return sortClassCount[0][0]五、程序运行结果
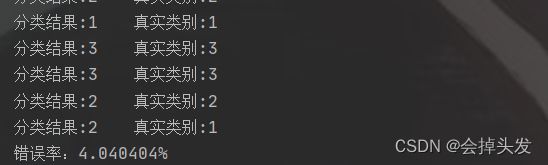
我们运行该算法可得到如下结果:
代码实现如下:
if __name__ == '__main__':
resultList = ['讨厌', '有些喜欢', '非常喜欢']
datingDataMat, datingLabels = file2matrix(r"C:\Users\86177\PycharmProjects\KNN\venv\dataset.txt")
normDataSet, ranges, minVals = autoNorm(datingDataMat)
# 取数据集的10%作为测试集
hoRatio = 0.10
m = normDataSet.shape[0]
numTestVecs = int(m * hoRatio)
errorCount = 0.0
for i in range(numTestVecs):
classifierResult = classify0(normDataSet[i, :], normDataSet[numTestVecs:m, :], datingLabels[numTestVecs:m], 4)
print("分类结果:%d\t真实类别:%d" % (classifierResult, datingLabels[i]))
if classifierResult !=datingLabels[i]:
errorCount += 1.0
print("错误率:%f%%"%(errorCount/float(numTestVecs)*100))
showdatas(datingDataMat, datingLabels)
六、总结
海伦约会预测的实现跟之前的简单KNN算法实现其实从本质上并没有大的区别,我们从核心的KNN算法代码部分可以看出,其实核心的算法部分并没有改变,整个实践与之前不同的就是数据的处理不同,并且导入的数据维度不同,我们这次对数据进行了归一化处理,并且数据的来源也是从文件导入,与之前不同。还做了数据的可视化,通过测试集还计算了算法的错误率。