python作图之plt.contour详解

plt.contour是python中用于画等高线的函数，这里介绍一下plt.contour的使用。

---

使用示例

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(-3, 3, 50)  # 生成连续数据
y = np.linspace(-3, 3, 50)  # 生成连续数据
X, Y = np.meshgrid(x, y)    
# 生成能够在坐标系中形成点阵的数组，这个可以去参考一下别的文章
# https://lixiaoqian.blog.csdn.net/article/details/81532855 这里讲的比较详细
Z = X**2 + Y**2     # 这里将高度设置为x^2+y^2，就能画一个圆形的等高线
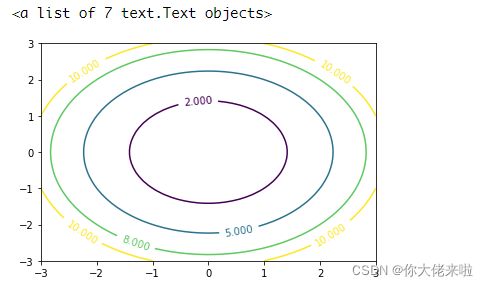
C=plt.contour(x, y,Z,[2,5,8,10])  # 画等高线 # 使用plt.contour(X, Y,Z,[2,5,8,10])也是没问题的
plt.clabel(C, inline=True, fontsize=10)

画出来的效果就是：

plt.contour()函数本身

plt.contour(X, Y, Z, [levels], **kwargs)

• plt就是matplotlib.pyplot
• X, Y表示的是坐标位置（这里是可选的，但是如果不传入的话就是python根据传入的高度数组(Z)的大小自动生成的坐标），一般很多会使用二维数组，但是实际上一维数组也可以的
• Z代表每个坐标对应的高度值，是一个二维数组，其中每个值表示的是每个坐标对应的高度 XYZ的实际数据构成可以参照上面的例子，在本地查看一下数据是长什么样
• levels有两种传入形式。一种是传入一个整数，这个整数表示你想绘制的等高线的条数，但是显示结果可能并不是完全和传入的整数的条数一样，是大致差不多的条数（可能相差一两条）（为什么是大致条数呢？可能是python帮你默认生成的比较合适的几条等高线吧）。还有一种方式就是传入一个包含高度值的一维数组，这样python便会画出传入的高度值对应的等高线。
• 其余的参数cmap, linewidths, linestyles等这里就不多介绍了

plt.contour()图中的坐标

由于一开始这里很混淆，因此在这里对坐标代表的内容进行一个解释。要解释这个问题，首先可以引入实际问题，比如一座山，一般来说从飞机上或者很高的地方观察这座山的话能看到这座山就像圆一样，如果抽象成平面的话就成为一个圆了（这里是指比较规整的山啊）。然后实际上等高线就是从这样很高的地方去想象的，通过一系列工具把相同高度的位置在一个平面上标注出来，相同高度的位置通过线连起来就形成了等高线。

如果把刚刚说的圆放在坐标系中，那么某个坐标(x,y)就表示观察到的这座山在平面视角来看所展现出来的位置，如下图：

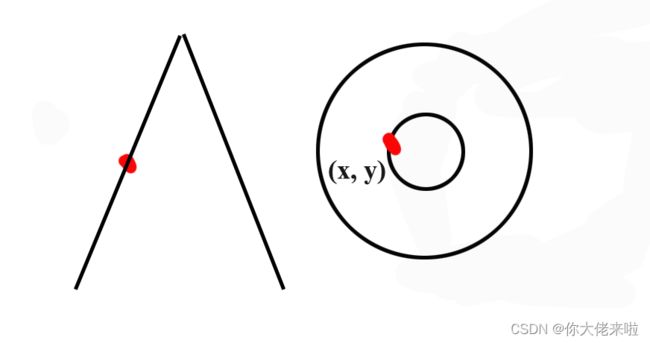
左边假设是一座山，上面的红色的点在平面视角来看的话就成为坐标系中的一个位置，此时高度已经在等高线图中反映不出来了，这也是为什么等高线的图需要标注高度值。

这里结合三维图来看会更加直观：将上面的圆形的等高线图的高度用三维图像展示出来，使用代码为：

from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np

x = np.linspace(-3, 3, 50)
y = np.linspace(-3, 3, 50)
X, Y = np.meshgrid(x, y)
Z = X**2 + Y**2 
C=plt.contour(x, y,Z,[2,5,8,10])
plt.clabel(C, inline=True, fontsize=10)

fig=plt.figure()
fig = plt.figure(figsize=(10,10))
ax1 = plt.axes(projection='3d')

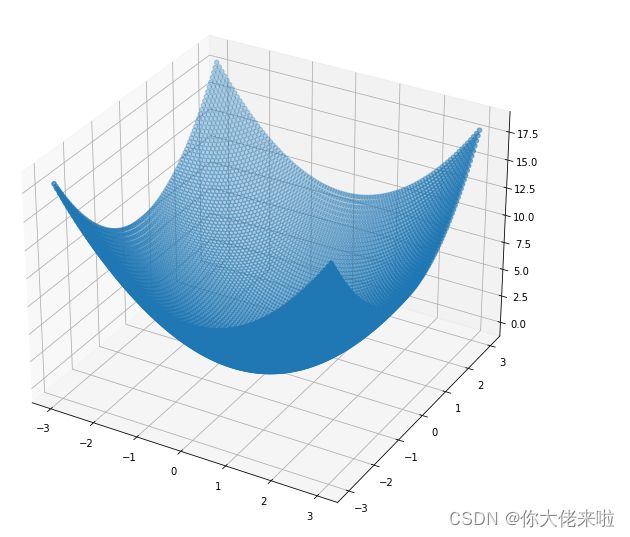
ax1.scatter3D(X,Y,z, cmap='Blues')

效果如下：

图中X,Y,Z都分别被转换为了三维坐标系中的坐标，形成了一个类似球形的一个部分的高度图。Z轴就是每个点对应的高度值，这里试想如果把整张图从最顶部投下到xy二维坐标系中，如果取开始的某几个固定的高度值（如2,5,8），那么这几个固定的高度值所对应的坐标在二维坐标系中连起来的话就成为了一条等高线。

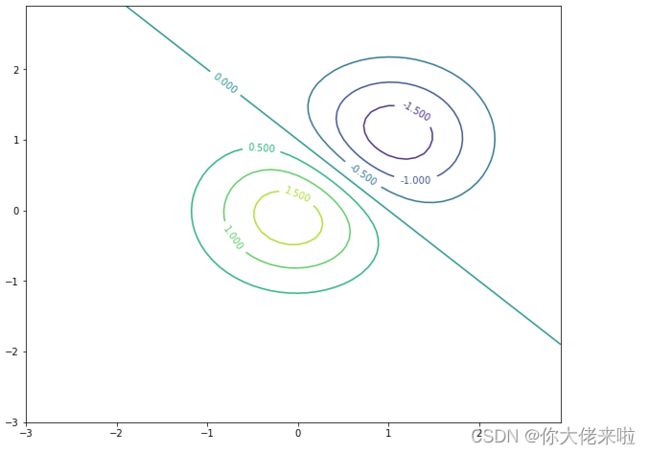
这里可以多看几个例子：

x = np.linspace(-3, 3, 50)
y = np.linspace(-3, 3, 50)
X, Y = np.meshgrid(x, y)
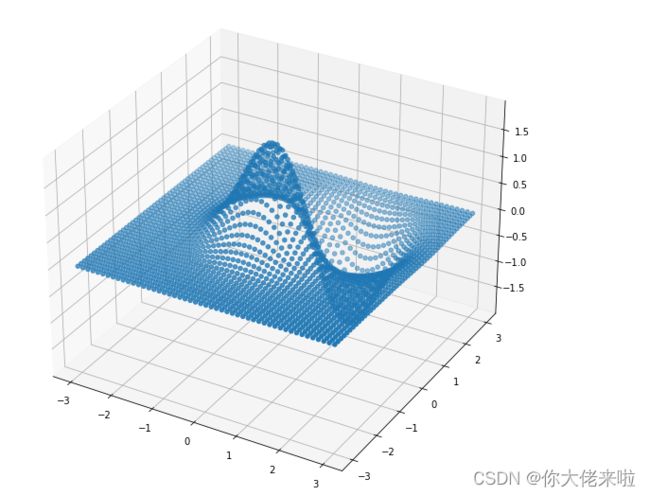
z = (np.exp(-X**2 - Y**2) - np.exp(-(X - 1)**2 - (Y - 1)**2))*2

fig=plt.figure()
fig = plt.figure(figsize=(10,10))
ax1 = plt.axes(projection='3d')
ax1.scatter3D(X,Y,z, cmap='Blues')

效果：
其二维图为：

叮！

不学不知道，学了才知道什么都不是想象的那么简单啊。

参考：https://blog.csdn.net/qq_42505705/article/details/88771942