【良心讲解】刘二大人第二讲课后习题
刘二大人(B站)第二章作业解析
本文针对刘二大人线性模型视频课后习题进行讲解
关于刘二大人得课上内容可登录下方网址查看:
刘二大人网课
课上代码
import numpy as np
import matplotlib.pyplot as plt
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
def forward(x):
return x*w
def loss(x, y):
y_pred = forward(x)
return (y_pred - y)*(y_pred-y)
# 穷举法
w_list = []
mse_list = []
for w in np.arange(0.0, 4.1, 0.1):
print("w=", w)
l_sum = 0
for x_val, y_val in zip(x_data, y_data):
y_pred_val = forward(x_val)
loss_val = loss(x_val, y_val)
l_sum += loss_val
print('\t', x_val, y_val, y_pred_val, loss_val)
print('MSE=', l_sum/3)
w_list.append(w)
mse_list.append(l_sum/3)
plt.plot(w_list,mse_list)
plt.ylabel('Loss')
plt.xlabel('w')
plt.show()
上述代码为课堂讲解代码,在此不做过多赘述,如有疑问可以私信作者或观看刘二大人网课视频。
一、线性模型
本文所写模型为:y=2x。
使用y=wx+b对模型进行分析绘图。
二、代码
1.引入库
代码如下:
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
2.定义变量
代码如下:
x_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]
W = np.arange(0.0,4.1,0.1)
B = np.arange(-2.0,2.1,0.1)
[w,b] = np.meshgrid(W,B)#建立网格化联系
l_sum = 0
下方为相关函数讲解:
numpy.meshgrid()函数讲解
3.定义函数
代码如下:
#验证函数
def forward(x):
return x * w + b
#损失函数
def loss(x,y):
y_pred = forward(x)
return (y_pred-y)**2
4.主函数
代码如下:
#主要计算过程
for x_val, y_val in zip(x_data, y_data):
y_pred_val = forward(x_val)
loss_val = loss(x_val, y_val)
l_sum += loss_val
print(l_sum.shape)
#绘图
fig = plt.figure()
ax = Axes3D(fig)
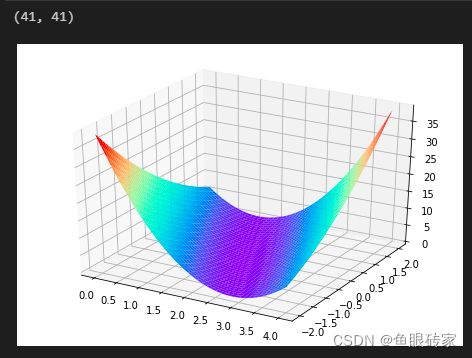
ax.plot_surface(w, b, l_sum/3,cmap='rainbow')
plt.show()
3D图绘制讲解博客:
python绘制3D图方法
5.总代码
为便于大家理解[w,b]如何同l_sum建立联系,对定义变量得位置进行调整。
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
#这里设函数为y=2x
x_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]
l_sum = 0
#W=np.arange(0.0,4.1,0.1)
#B=np.arange(-2.0,2.1,0.1)
#[w,b]=np.meshgrid(W,B)
#将该组数据引入forward函数中定义,便于理解。
def forward(x):#注意数和向量可以相乘,结果为向量
W=np.arange(0.0,4.1,0.1)
B=np.arange(-2.0,2.1,0.1)
[w,b]=np.meshgrid(W,B)
#变量[w,b]再后续计算中仍可使用,非形参
return x * w + b
#此时返回向量为40个点所对应得预测值向量,其中有40个元素
def loss(x,y):
y_pred = forward(x)
return (y_pred-y)**2
for x_val, y_val in zip(x_data, y_data):
y_pred_val = forward(x_val)#调用函数生成w,b并返还预测值向量
loss_val = loss(x_val, y_val)#返回损失值向量
l_sum += loss_val#损失值求和时,自动扩充为numpy向量
print(l_sum.shape)#观察向量形状
fig = plt.figure()
ax = Axes3D(fig)
ax.plot_surface(w, b, l_sum/3,cmap='rainbow')
#运行前已使用过forward函数,已对[w,b]进行定义,所以无需对w和b再定义
plt.show()