POJ-3693 Maximum repetition substring 后缀数组

　　题目链接：http://poj.org/problem?id=3693

　　求字符串的重复次数最多的且字典序最小的字串。

　　很不错的题目。罗穗骞大牛论文的模板题，摘了Neo / Add ~0U>>1大牛的详细题解，如下：

　　首先求第一问最大重复数。从N的范围来看O(N^2)虽不靠谱，但是起码能带来些有用的启示。方法有二，一是枚举开头位置求重复长度；二是枚举重复长度求开头位置。

第一种方法求最大重复数的方法MS也只有枚举重复长度然后去判……所以说我们从第二个方法入手。O(N^2)的方法是再枚举开头位置。我们来考虑一下能不能少枚举一些开头位置——更确切地说，能不能只枚举一些特殊位置，设当前枚举的长度为L，能不能只枚举0，L，2L，……这样的位置。见下图：

                         

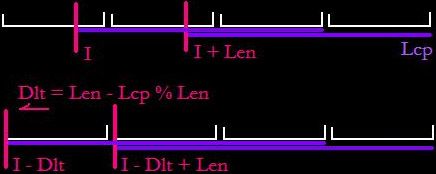
　　首先明确，枚举长度Len的时候，从一个位置求出的Lcp值表明从此处开始重复数为floor(Lcp / Len) + 1。

　　然后容易发现的问题就是，可能从某个枚举位置向前移动“一点”能够多一个周期，从而使重复数增加。从图上来看，这种状况发生的条件就是Lcp比满足这个重复数“必需的Lcp”要多，也就是Lcp % Len ≠ 0。不难发现，这时候我们向前移动Len - Lcp % Len的话，如果有下一个周期就会进去，否则也不会引起新的变化。所以说这种方法可行。

　　这样的话复杂度为n(1 + 1/2 + 1/3 + ... + 1/n) = O(nlogn)。有一个显而易见的优化，那就是只需要枚举到floor(n / 2)即可。但是后面的部分也少不了多少……

　　第二问是求最小字典序的答案。我采用了这样一种方法，那就是在第一步中记录能够达到最大重复数的重复长度的集合，然后按照sa[1]，sa[2]，sa[3]，……的顺序去暴力枚举，每到一个位置就从小到大地判重复长度的集合中有没有可行的，如果有一个可行的就立即输出结果并退出。这样的做法能够保证正确性，虽然最坏情况下仍然有可能退化到O(n^2)，但是要构造这样一组数据是比较困难的（得一直枚举到最后一个后缀，还得从1到Len / 2都能满足最大重复数）。对于非特殊构造的数据这一步的复杂度几乎是O(n)，于是这个题就可以水过了。

　　我的代码：

  1 //STATUS:C++_AC_422MS_11232KB

  2 #include<stdio.h>

  3 #include<stdlib.h>

  4 #include<string.h>

  5 #include<math.h>

  6 #include<iostream>

  7 #include<string>

  8 #include<algorithm>

  9 #include<vector>

 10 #include<queue>

 11 #include<stack>

 12 #include<map>

 13 using namespace std;

 14 #define LL __int64

 15 #define pii pair<int,int>

 16 #define mem(a,b) memset(a,b,sizeof(a))

 17 #define lson l,mid,rt<<1

 18 #define rson mid+1,r,rt<<1|1

 19 #define PI acos(-1.0)

 20 const int N=100010,INF=0x3f3f3f3f,MOD=10000,STA=8000010;

 21 //const LL LNF=0x3f3f3f3f3f3f3f3f;

 22 const double DNF=1e13;

 23 //

 24 inline int Max(int a,int b){return a>b?a:b;}

 25 inline int Min(int a,int b){return a<b?a:b;}

 26 void swap(int& a,int& b){int t=a;a=b;b=t;}

 27 void swap(LL& a,LL& b){LL t=a;a=b;b=t;}

 28 //

 29 

 30 char s[N];

 31 int d[N][20];

 32 int num[N];

 33 int sa[N],t1[N],t2[N],c[N],rank[N],height[N];

 34 int n,m;

 35 

 36 void build_sa(int s[],int n,int m)

 37 {

 38     int i,k,p,*x=t1,*y=t2;

 39     //第一轮基数排序

 40     for(i=0;i<m;i++)c[i]=0;

 41     for(i=0;i<n;i++)c[x[i]=s[i]]++;

 42     for(i=1;i<m;i++)c[i]+=c[i-1];

 43     for(i=n-1;i>=0;i--)sa[--c[x[i]]]=i;

 44     for(k=1;k<=n;k<<=1){

 45         p=0;

 46         //直接利用sa数组排序第二关键字

 47         for(i=n-k;i<n;i++)y[p++]=i;

 48         for(i=0;i<n;i++)if(sa[i]>=k)y[p++]=sa[i]-k;

 49         //基数排序第一关键字

 50         for(i=0;i<m;i++)c[i]=0;

 51         for(i=0;i<n;i++)c[x[y[i]]]++;

 52         for(i=1;i<m;i++)c[i]+=c[i-1];

 53         for(i=n-1;i>=0;i--)sa[--c[x[y[i]]]]=y[i];

 54         //根据sa和x数组计算新的x数组

 55         swap(x,y);

 56         p=1;x[sa[0]]=0;

 57         for(i=1;i<n;i++)

 58             x[sa[i]]=y[sa[i-1]]==y[sa[i]] && y[sa[i-1]+k]==y[sa[i]+k]?p-1:p++;

 59         if(p>=n)break;   //已经排好序，直接退出

 60         m=p;     //下次基数排序的最大值

 61     }

 62 }

 63 

 64 void getHeight(int s[],int n)

 65 {

 66     int i,j,k=0;

 67     for(i=0;i<=n;i++)rank[sa[i]]=i;

 68     for(i=0;i<n;i++){

 69         if(k)k--;

 70         j=sa[rank[i]-1];

 71         while(s[i+k]==s[j+k])k++;

 72         height[rank[i]]=k;

 73     }

 74 }

 75 

 76 void rmq_init(int a[])

 77 {

 78     int i,j;

 79     for(i=1;i<=n;i++)d[i][0]=a[i];

 80     for(j=1;(1<<j)<=n;j++){

 81         for(i=1;i+(1<<j)-1<=n;i++){

 82             d[i][j]=Min(d[i][j-1],d[i+(1<<(j-1))][j-1]);

 83         }

 84     }

 85 }

 86 

 87 int rmq(int l,int r)

 88 {

 89     int k=0;

 90     while((1<<(k+1))<=r-l+1)k++;

 91     return Min(d[l][k],d[r-(1<<k)+1][k]);

 92 }

 93 

 94 int lcp(int a,int b)

 95 {

 96     if(a==b)return n-a;

 97     int ra=rank[a],rb=rank[b];

 98     if(ra>rb)swap(ra,rb);

 99     ra++;

100     return rmq(ra,rb);

101 }

102 

103 int main()

104 {

105  //   freopen("in.txt","r",stdin);

106     int i,j,sz=1,hig,ans[N],cnt,fre,wide,t,ss,ok;

107     while(~scanf("%s",s) && (s[0]!='#' || s[1]) )

108     {

109         n=strlen(s);

110         for(i=0;i<n;i++){

111             num[i]=s[i]-'a'+1;

112         }

113         num[n]=0;

114         m=27;

115         build_sa(num,n+1,m);

116         getHeight(num,n);

117         rmq_init(height);

118 

119         hig=0;

120         for(i=1;i<=n/2;i++){

121             for(j=0;j+i<n;j+=i){

122                 wide=lcp(j,j+i);

123                 fre=wide/i+1;

124                 t=j-(i-wide%i);

125                 if(t>=0 && wide%i){

126                     wide=lcp(t,t+i);

127                     fre=Max(fre,wide/i+1);

128                 }

129                 if(fre>hig){

130                     hig=fre;

131                     cnt=0;

132                     ans[cnt++]=i;

133                 }

134                 else if(fre==hig){

135                     ans[cnt++]=i;

136                 }

137             }

138         }

139 

140         ok=0;

141         for(i=1;i<=n;i++){

142             for(j=0;j<cnt;j++){

143                 if(sa[i]+ans[j]>=n)continue;

144                 wide=lcp(sa[i],sa[i]+ans[j]);

145                 if(wide/ans[j]+1==hig){

146                     ss=sa[i];

147                     s[ss+hig*ans[j]]=0;

148                     ok=1;

149                     break;

150                 }

151             }

152             if(ok)break;

153         }

154 

155         printf("Case %d: %s\n",sz++,s+ss);

156     }

157     return 0;

158 }