POJ-2778 DNA Sequence AC自动机+矩阵二分

　　题目链接：http://poj.org/problem?id=2778

　　[摘自Matrix67]  题目大意是，检测所有可能的n位DNA串有多少个DNA串中不含有指定的病毒片段。合法的DNA只能由ACTG四个字符构成。题目将给出10个以内的病毒片段，每个片段长度不超过10。数据规模n<=2 000 000 000。
　　下面的讲解中我们以ATC,AAA,GGC,CT这四个病毒片段为例，说明怎样像上面的题一样通过构图将问题转化为例题8。我们找出所有病毒片段的前缀，把n位DNA分为以下7类：以AT结尾、以AA结尾、以GG结尾、以?A结尾、以?G结尾、以?C结尾和以??结尾。其中问号表示“其它情况”，它可以是任一字母，只要这个字母不会让它所在的串成为某个病毒的前缀。显然，这些分类是全集的一个划分（交集为空，并集为全集）。现在，假如我们已经知道了长度为n-1的各类DNA中符合要求的DNA个数，我们需要求出长度为n时各类DNA的个数。我们可以根据各类型间的转移构造一个边上带权的有向图。例如，从AT不能转移到AA，从AT转移到??有4种方法（后面加任一字母），从?A转移到AA有1种方案（后面加个A），从?A转移到??有2种方案（后面加G或C），从GG到??有2种方案（后面加C将构成病毒片段，不合法，只能加A和T）等等。这个图的构造过程类似于用有限状态自动机做串匹配。然后，我们就把这个图转化成矩阵，让这个矩阵自乘n次即可。最后输出的是从??状态到所有其它状态的路径数总和。
　　题目中的数据规模保证前缀数不超过100，一次矩阵乘法是三方的，一共要乘log(n)次。因此这题总的复杂度是100^3 * log(n)，AC了。

　　Example:　　　　　　　

　　　　　　2 3

　　　　　　AG

　　　　　　CG

　　状态转移图：

　　　　　　　

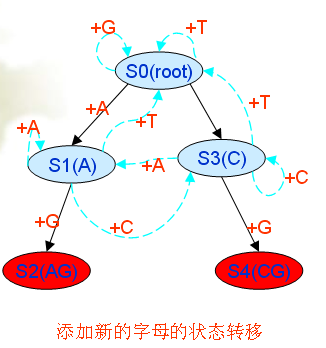
　　要注意当前前缀 i 匹配的前缀 j 可能不是可行的前缀。

  1 //STATUS:C++_AC_313MS_624KB

  2 #include<stdio.h>

  3 #include<stdlib.h>

  4 #include<string.h>

  5 #include<math.h>

  6 #include<iostream>

  7 #include<string>

  8 #include<algorithm>

  9 #include<vector>

 10 #include<queue>

 11 #include<stack>

 12 #include<map>

 13 #include<set>

 14 using namespace std;

 15 //define

 16 #define pii pair<int,int>

 17 #define mem(a,b) memset(a,b,sizeof(a))

 18 #define lson l,mid,rt<<1

 19 #define rson mid+1,r,rt<<1|1

 20 #define PI acos(-1.0)

 21 //typedef

 22 typedef __int64 LL;

 23 typedef unsigned __int64 ULL;

 24 //const

 25 const int N=101;

 26 const int INF=0x3f3f3f3f;

 27 const int MOD=100000,STA=8000010;

 28 const LL LNF=1LL<<60;

 29 const double EPS=1e-8;

 30 const double OO=1e15;

 31 //Daily Use ...

 32 template<class T> T gcd(T a,T b){return b?gcd(b,a%b):a;}

 33 template<class T> T lcm(T a,T b){return a/gcd(a,b)*b;}

 34 template<class T> inline T Min(T a,T b){return a<b?a:b;}

 35 template<class T> inline T Max(T a,T b){return a>b?a:b;}

 36 template<class T> inline T Min(T a,T b,T c){return min(min(a, b),c);}

 37 template<class T> inline T Max(T a,T b,T c){return max(max(a, b),c);}

 38 template<class T> inline T Min(T a,T b,T c,T d){return min(min(a, b),min(c,d));}

 39 template<class T> inline T Max(T a,T b,T c,T d){return max(max(a, b),max(c,d));}

 40 //End

 41 

 42 int idx[N];

 43 int ch[N][4];

 44 int val[N],f[N],sta[N];

 45 int sz,n,m;

 46 int size;

 47 

 48 struct Matrix{

 49     LL ma[N][N];

 50     Matrix friend operator * (const Matrix a,const Matrix b){

 51         Matrix ret;

 52         mem(ret.ma,0);

 53         int i,j,k;

 54         for(k=0;k<size;k++)

 55             for(i=0;i<size;i++)

 56                 for(j=0;j<size;j++)

 57                     ret.ma[i][j]=(ret.ma[i][j]+a.ma[i][k]*b.ma[k][j])%MOD;

 58         return ret;

 59     }

 60 }ans,mta;

 61 

 62 void mutilpow(LL k)

 63 {

 64     int i,j;

 65     mem(ans.ma,0);

 66     for(i=0;i<size;i++)

 67         ans.ma[i][i]=1;

 68     for(;k;k>>=1){

 69         if(k&1)ans=ans*mta;

 70         mta=mta*mta;

 71     }

 72 }

 73 

 74 void init(){sz=1;mem(ch[0],0);}

 75 

 76 void insert(char *s,int v){

 77     int i,len=strlen(s),id,u=0;

 78     for(i=0;i<len;i++){

 79         id=idx[s[i]];

 80         if(!ch[u][id]){

 81             mem(ch[sz],0);

 82             val[sz]=0;

 83             ch[u][id]=sz++;

 84         }

 85         u=ch[u][id];

 86     }

 87     val[u]=v;

 88 }

 89 

 90 void getFail()

 91 {

 92     int u,v,r,c;

 93     queue<int> q;

 94     mem(mta.ma,0);

 95     f[0]=0;

 96     sta[0]=size++;

 97     for(c=0;c<4;c++){

 98         u=ch[0][c];

 99         if(u){

100             f[u]=0;q.push(u);

101             if(!val[u]){

102                 sta[u]=size++;

103                 mta.ma[0][sta[u]]++;

104             }

105         }

106         else mta.ma[0][0]++;

107     }

108     while(!q.empty()){

109         r=q.front();q.pop();

110         if(sta[r]==-1)continue;

111         for(c=0;c<4;c++){

112             u=ch[r][c];

113             if(!u){

114                 v=ch[r][c]=ch[f[r]][c];

115                 if(sta[v]==-1)continue;

116                 mta.ma[sta[r]][sta[v]]++;

117             }

118             else {

119                 q.push(u);

120                 v=f[r];

121                 while(v && !ch[v][c])v=f[v];

122                 f[u]=ch[v][c];

123                 if(val[u] || sta[f[u]]==-1)continue;

124                 sta[u]=size++;

125                 mta.ma[sta[r]][sta[u]]++;

126             }

127         }

128     }

129 }

130 

131 int main()

132 {

133  //   freopen("in.txt","r",stdin);

134     int i,j;

135     LL sum;

136     char s[20];

137     idx['A']=0;idx['C']=1;idx['T']=2,idx['G']=3;

138     while(~scanf("%d%d",&m,&n))

139     {

140         init();

141         for(i=0;i<m;i++){

142             scanf("%s",s);

143             insert(s,1);

144         }

145 

146         mem(sta,-1);

147         size=0;

148         getFail();

149         mutilpow(n);

150         for(i=sum=0;i<size;i++){

151             sum+=ans.ma[0][i];

152         }

153 

154         printf("%I64d\n",sum%MOD);

155     }

156     return 0;

157 }