波士顿房价预测（TensorFlow2.9实践）

波士顿房价预测（TensorFlow2.9实践）

波士顿房价数据集包括506个样本，每个样本包括12个特征变量和该地区的平均房价。房价（单价）显然和多个特征变量相关，不是单变量线性回归（一元线性回归）问题，选择多个特征变量来建立线性方程，这就是多变量线性回归（多元线性回归）问题。本文探讨了使用TensorFlow2.9+多元线性回归，解决波士顿房价预测问题。

使用TensorFlow进行算法设计与训练的核心步骤：

（1）准备数据

（2）构建模型

（3）训练模型

（4）进行预测

一、数据读取

数据集解读

读取数据

import tensorflow as tf   #导入Tensorflow
import numpy as np       #导入numpy
import matplotlib.pyplot as plt#导入matplotlib
%matplotlib inline
import pandas as pd    #导入pandas
from sklearn.utils import shuffle           #导入sklearn的shuffle
from sklearn.preprocessing import scale    #导入sklearn的scale
print("Tensorflow版本是:",tf.__version__)    #显示版本

Tensorflow版本是: 2.9.1

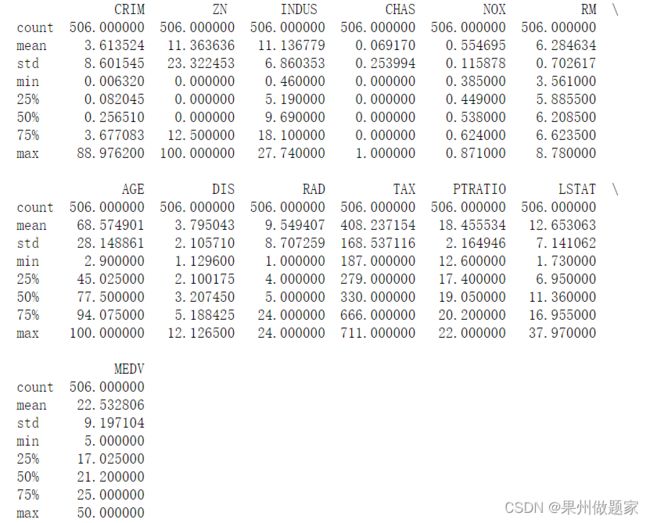
通过pandas读取数据文件，列出统计概述：

df=pd.read_csv("boston.csv",header=0)
print(df.describe())

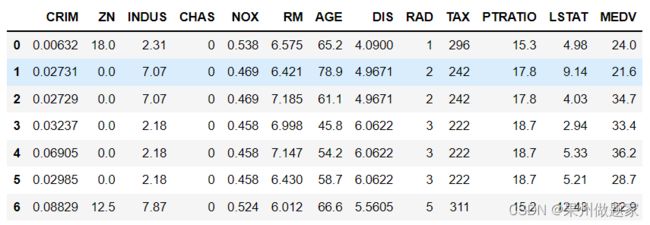
显示前3条数据:

df.head(3)  #显示前3条数据

显示后3条数据：

df.tail(3)  #显示后3条数据

二、数据准备

#获取数据集的值
ds=df.values   #df.values以np.array形式返回数据集的值
print(ds.shape)   #查看数据的形状

(506, 13)

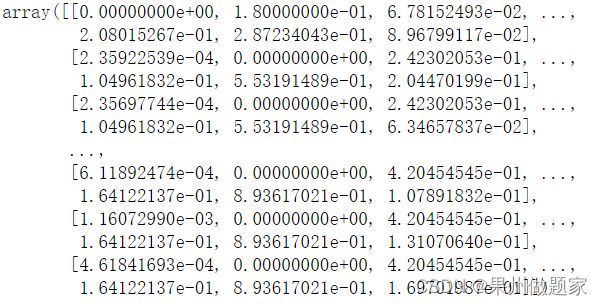
查看数据集的值：

print(ds)    #查看数据集的值

三、划分特征数据和标签数据

# x_data 为归一化前的前12列特征数据
x_data = ds[:,:12]
# y_data 为最后1列标签数据
y_data = ds[:,12]
print('x_data shape=',x_data.shape)
print('y_data shape=',y_data.shape)

x_data shape= (506, 12)
y_data shape= (506,)

四、特征数据归一化

考虑不同特征值取值范围大小的影响，需要对特征数据归一化。

#对特征数据【0到11】列做（0-1)归一化
for i in range(12):
    x_data[:,i]=(x_data[:,i]-x_data[:,i].min())/(x_data[:,i].max()-x_data[:,i].min())
x_data

五、数据集划分

构建和训练机器学习模型是希望对新的数据做出良好预测。如何去保证训练的实效，可以应对以前未见过的数据呢？全部带标签的数据参与模型训练，真的好吗？

划分数据集的方法：

一种方法是将数据集分成两个子集：

• 训练集 - 用于训练模型的子集
• 测试集 - 用于测试模型的子集

通常，在测试集上表现是否良好是衡量能否在新数据上表现良好的有用指标，前提是：
测试集足够大，不会反复使用相同的测试集来作假。

拆分数据：

将单个数据集拆分为一个训练集和一个测试集

确保测试集满足以下两个条件：
（1）规模足够大，可产生具有统计意义的结果
（2）能代表整个数据集，测试集的特征应该与训练集的特征相同

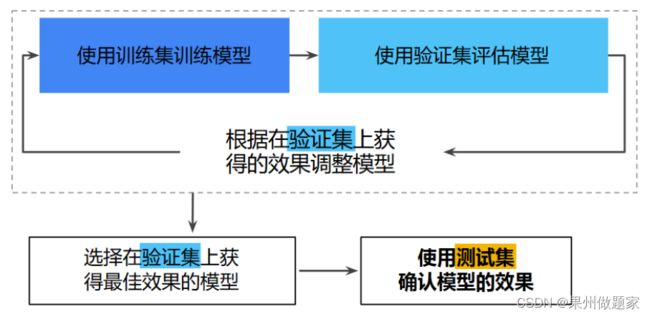
工作流程：

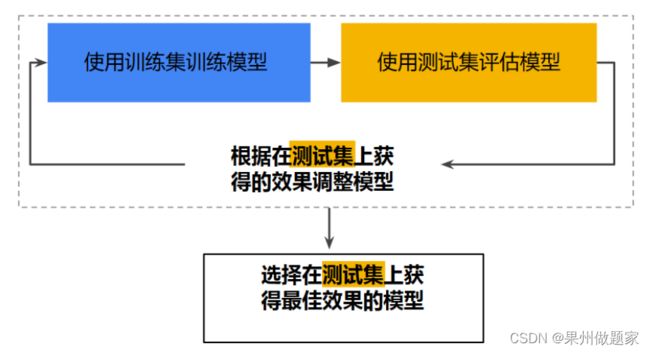
问题思考：
使用测试集和训练集来推动模型开发迭代的流程。
在每次迭代时，都会对训练数据进行训练并评估测试数据，并以基于测试数据的评估结果为指导来选择和更改各种模型超参数，例如学习速率和特征。这种方法是否存在问题？
问题在于：多次重复执行该流程可能导致模型不知不觉地拟合了特定测试集的特性。

新的数据划分：

通过将数据集划分为三个子集，可以大幅降低过拟合的发生几率：

使用验证集评估训练集的效果。
在模型“通过”验证集之后，使用测试集再次检查评估结果。

新的工作流程：

划分训练集、验证集和测试集：

train_num = 300    #训练集的数目
valid_num = 100    #验证集的数目
test_num = len(x_data) - train_num - valid_num #测试集的数日 = 506-训练集的数日–验证集的数月

#训练集划分
x_train = x_data[:train_num]
y_train = y_data[:train_num]

#验证集划分
x_valid = x_data[train_num:train_num+valid_num]
y_valid = y_data[train_num:train_num+valid_num]

#测试集划分
x_test = x_data[train_num+valid_num:train_num+valid_num+test_num]
y_test = y_data[train_num+valid_num:train_num+valid_num+test_num]

六、转换数据类型

转换为tf.float32数据类型，后面求损失时要和变量W执行tf.matmul操作

x_train = tf.cast(x_train,dtype=tf.float32)
x_valid = tf.cast(x_valid,dtype=tf.float32)
x_test = tf.cast(x_test,dtype=tf.float32)

七、构建模型

def model(x,w,b):
    return tf.matmul(x,w)+b

八、创建待优化变量

W = tf.Variable(tf.random.normal([12,1],mean=0.0,stddev=1.0,dtype=tf.float32))
B= tf.Variable(tf.zeros(1),dtype = tf.float32)
print(W)
print(B)

九、模型训练

9.1 设置超参数

training_epochs = 50  #迭代次数
learning_rate = 0.001  #学习率
batch_size = 10  #批量训练一次的样本数

9.2 定义损失函数

#采用均方差作为损失函数

def loss(x,y,w,b):
    err = model(x, w,b) - y       #计算模型预测值和标签值的差异
    squared_err = tf.square(err)  #求平方，得出方差
    return tf.reduce_mean(squared_err) #求均值，得出均方差.

9.3 定义梯度函数

#计算样本数据[x,y]在参数[w, b]点上的梯度

def grad(x,y,w,b):
    with tf.GradientTape() as tape:
        loss_= loss(x,y,w,b)
    return tape.gradient(loss_,[w,b]) #返回梯度向量

9.4 选择优化器

optimizer = tf.keras.optimizers.SGD(learning_rate) #创建优化器，指定学习率

9.5 迭代训练

loss_list_train = []  #用于保存训练集1oss值的列表
loss_list_valid = []  #用于保存验证集loss值的列表
total_step = int(train_num/batch_size)

for epoch in range(training_epochs):
    for step in range(total_step):
        xs = x_train[step*batch_size:(step+1)*batch_size,:]
        ys = y_train[step*batch_size:(step+1)*batch_size]
        
        grads = grad(xs,ys,W,B)   #计算梯度
        optimizer.apply_gradients(zip(grads,[W,B])) #优化器根据梯度自动调整变量w和b
        
    loss_train = loss(x_train,y_train,W,B).numpy()   #计算当前轮训练损失
    loss_valid = loss(x_valid,y_valid,W,B).numpy()   #计算当前轮验证损失
    loss_list_train.append(loss_train)
    loss_list_valid.append(loss_valid)
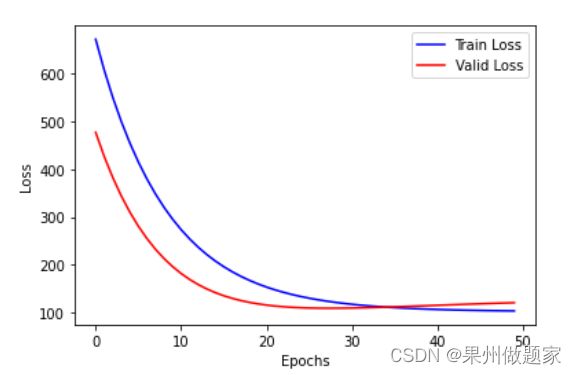
    print("epoch={:3d},train_loss={:.4f},valid_loss={:.4f}".format(epoch+1,loss_train,loss_valid))

epoch= 1,train_loss=587.1567,valid_loss=414.5585
epoch= 2,train_loss=461.1470,valid_loss=304.6138
epoch= 3,train_loss=366.7652,valid_loss=227.8302
epoch= 4,train_loss=296.0490,valid_loss=175.0670
epoch= 5,train_loss=243.0432,valid_loss=139.5983
epoch= 6,train_loss=203.2935,valid_loss=116.4885
epoch= 7,train_loss=173.4678,valid_loss=102.1276
epoch= 8,train_loss=151.0732,valid_loss=93.8853
epoch= 9,train_loss=134.2448,valid_loss=89.8543
epoch= 10,train_loss=121.5869,valid_loss=88.6597
epoch= 11,train_loss=112.0550,valid_loss=89.3172
epoch= 12,train_loss=104.8675,valid_loss=91.1287
epoch= 13,train_loss=99.4389,valid_loss=93.6048
epoch= 14,train_loss=95.3310,valid_loss=96.4073
epoch= 15,train_loss=92.2155,valid_loss=99.3077
epoch= 16,train_loss=89.8464,valid_loss=102.1555
epoch= 17,train_loss=88.0393,valid_loss=104.8561
epoch= 18,train_loss=86.6560,valid_loss=107.3541
epoch= 19,train_loss=85.5927,valid_loss=109.6212
epoch= 20,train_loss=84.7715,valid_loss=111.6475
epoch= 21,train_loss=84.1340,valid_loss=113.4355
epoch= 22,train_loss=83.6362,valid_loss=114.9954
epoch= 23,train_loss=83.2449,valid_loss=116.3418
epoch= 24,train_loss=82.9353,valid_loss=117.4922
epoch= 25,train_loss=82.6886,valid_loss=118.4646
epoch= 26,train_loss=82.4904,valid_loss=119.2775
epoch= 27,train_loss=82.3301,valid_loss=119.9482
epoch= 28,train_loss=82.1996,valid_loss=120.4934
epoch= 29,train_loss=82.0925,valid_loss=120.9283
epoch= 30,train_loss=82.0043,valid_loss=121.2668
epoch= 31,train_loss=81.9312,valid_loss=121.5214
epoch= 32,train_loss=81.8704,valid_loss=121.7035
epoch= 33,train_loss=81.8199,valid_loss=121.8229
epoch= 34,train_loss=81.7781,valid_loss=121.8884
epoch= 35,train_loss=81.7434,valid_loss=121.9079
epoch= 36,train_loss=81.7151,valid_loss=121.8881
epoch= 37,train_loss=81.6921,valid_loss=121.8350
epoch= 38,train_loss=81.6740,valid_loss=121.7537
epoch= 39,train_loss=81.6602,valid_loss=121.6488
epoch= 40,train_loss=81.6503,valid_loss=121.5241
epoch= 41,train_loss=81.6439,valid_loss=121.3830
epoch= 42,train_loss=81.6407,valid_loss=121.2285
epoch= 43,train_loss=81.6406,valid_loss=121.0630
epoch= 44,train_loss=81.6432,valid_loss=120.8886
epoch= 45,train_loss=81.6484,valid_loss=120.7074
epoch= 46,train_loss=81.6561,valid_loss=120.5208
epoch= 47,train_loss=81.6661,valid_loss=120.3301
epoch= 48,train_loss=81.6783,valid_loss=120.1367
epoch= 49,train_loss=81.6926,valid_loss=119.9414
epoch= 50,train_loss=81.7088,valid_loss=119.7451

十、可视化损失值

# 可视化损失值
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.plot(loss_list_train,'blue',label="Train Loss")
plt.plot(loss_list_valid,'red',label="Valid Loss")
plt.legend(loc=1)   #通过参数1oc指定图例位置

十一、查看测试集损失值

print("Test_loss:{:.4f}".format(loss(x_test,y_test,W,B).numpy()))

Test_loss:114.1834

十二、模型应用

测试集里随机选一条：

test_house_id = np.random.randint(0,test_num)
y = y_test[test_house_id]
y_pred = model(x_test,W,B)[test_house_id]
y_predit=tf.reshape(y_pred,()).numpy()
print("House id",test_house_id, "Actual value",y,"Predicted value ",y_predit)

House id 70 Actual value 19.9 Predicted value 25.09165

完整代码：

import tensorflow as tf   #导入Tensorflow
import numpy as np       #导入numpy
import matplotlib.pyplot as plt#导入matplotlib
#在Jupyter中，使用matplotlib显示图像需要设置为 inline 模式，否则不会在网页里显示图像
%matplotlib inline
import pandas as pd    #导入pandas
from sklearn.utils import shuffle           #导入sklearn的shuffle
from sklearn.preprocessing import scale    #导入sklearn的scale

def model(x,w,b):
    return tf.matmul(x,w)+b

#采用均方差作为损失函数
def loss(x,y,w,b):
    err = model(x, w,b) - y       #计算模型预测值和标签值的差异
    squared_err = tf.square(err)  #求平方，得出方差
    return tf.reduce_mean(squared_err) #求均值，得出均方差.df=pd.read_csv("boston.csv",header=0)

#计算样本数据[x,y]在参数[w, b]点上的梯度
def grad(x,y,w,b):
    with tf.GradientTape() as tape:
        loss_= loss(x,y,w,b)
    return tape.gradient(loss_,[w,b]) #返回梯度向量

#获取数据集的值
ds=df.values   #df.values以np.array形式返回数据集的值

# x_data 为归一化后的前12列特征数据
x_data = ds[:,:12]
# y_data 为最后1列标签数据
y_data = ds[:,12]
#对特征数据【0到11】列做（0-1)归一化
for i in range(12):
    x_data[:,i]=(x_data[:,i]-x_data[:,i].min())/(x_data[:,i].max()-x_data[:,i].min())

train_num = 300    #训练集的数目
valid_num = 100    #验证集的数目
test_num = len(x_data) - train_num - valid_num #测试集的数目 = 506-训练集的数目–验证集的数目

#训练集划分
x_train = x_data[:train_num]
y_train = y_data[:train_num]

#验证集划分
x_valid = x_data[train_num:train_num+valid_num]
y_valid = y_data[train_num:train_num+valid_num]

#测试集划分
x_test = x_data[train_num+valid_num:train_num+valid_num+test_num]
y_test = y_data[train_num+valid_num:train_num+valid_num+test_num]

#转换数据类型
x_train = tf.cast(x_train,dtype=tf.float32)
x_valid = tf.cast(x_valid,dtype=tf.float32)
x_test = tf.cast(x_test,dtype=tf.float32)

#创建待优化变量
W = tf.Variable(tf.random.normal([12,1],mean=0.0,stddev=1.0,dtype=tf.float32))
B= tf.Variable(tf.zeros(1),dtype = tf.float32)

#设置超参数
training_epochs = 50  #迭代次数
learning_rate = 0.001  #学习率
batch_size = 10  #批量训练一次的样本数

optimizer = tf.keras.optimizers.SGD(learning_rate) #创建优化器，指定学习率

#迭代训练
loss_list_train = []  #用于保存训练集1oss值的列表
loss_list_valid = []  #用于保存验证集loss值的列表
total_step = int(train_num/batch_size)

for epoch in range(training_epochs):
    for step in range(total_step):
        xs = x_train[step*batch_size:(step+1)*batch_size,:]
        ys = y_train[step*batch_size:(step+1)*batch_size]
        
        grads = grad(xs,ys,W,B)   #计算梯度
        optimizer.apply_gradients(zip(grads,[W,B])) #优化器根据梯度自动调整变量w和b
        
    loss_train = loss(x_train,y_train,W,B).numpy()   #计算当前轮训练损失
    loss_valid = loss(x_valid,y_valid,W,B).numpy()   #计算当前轮验证损失
    loss_list_train.append(loss_train)
    loss_list_valid.append(loss_valid)
    print("epoch={:3d},train_loss={:.4f},valid_loss={:.4f}".format(epoch+1,loss_train,loss_valid))