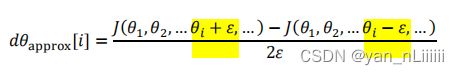深度学习课程自学笔记整理(二)——一些自己总结记录的结论和小tips等
注:本人已经学完了吴恩达老师机器学习深度学习的全部课程,整理出来的知识点是比较笼统的、自己总结的一些结论和经验,发在这里主要是为了方便自己复习翻阅,已经学完大部分课程或者对深度学习有了一定基础的uu可以阅读下~欢迎批评指正。
笔记一:吴恩达深度学习课程自学笔记整理(一)
深度学习的实践层面
Train/Dev/Test sets
- 只有训练集和测试集:七三分
- 有验证集且总数量不多:六二二分
- 有验证集且总数量很多-百万级别:大部分作交叉验证集
假设我们有 100 万条数据,其中 1 万条作为验证集,1 万条作为测试集,即:训练集占98%,验证集和测试集各占 1%。对于数据量过百万的应用,训练集可以占到 99.5%,验证和测试集各占 0.25%,或者验证集占 0.4%,测试集占 0.1%。 - 根据经验,要确保验证集和测试集的数据来自同一分布,关于这个问题老师在后面会多讲一些。因为要用验证集来评估不同的模型,尽可能地优化性能,如果验证集和测试集来自同一个分布就会很好。
- 最后一点,就算没有测试集也不要紧,测试集的目的是对最终所选定的神经网络系统做出无偏估计,如果不需要无偏估计,也可以不设置测试集。所以如果只有验证集,没有测试集,我们要做的就是,在训练集上训练、尝试不同的模型框架,在验证集上评估这些模型,然后迭代并选出适用的模型。这是因为验证集中已经涵盖测试集数据,其不再提供无偏性能评估。
在机器学习中,如果只有一个训练集和一个验证集,而没有独立的测试集,遇到这种情况,训练集还被人们称为训练集,而验证集则被称为测试集,不过在实际应用中,人们只是把测试集当成简单交叉验证集使用,并没有完全实现该术语的功能。
如果某团队跟你说他们只设置了一个训练集和一个测试集,我会很谨慎,心想他们是不是真的有训练验证集,我会让这些团队改变叫法,改称其为“训练验证集”,而不是“训练测试集”。即便我认为“训练验证集“在专业用词上更准确,实际上,如果你不需要无偏评估算法性能,那么这样是可以的。
偏差、方差
高偏差(high bias)的情况,“欠拟合”(underfitting)
高方差(high variance)的情况,数据过度拟(overfitting)
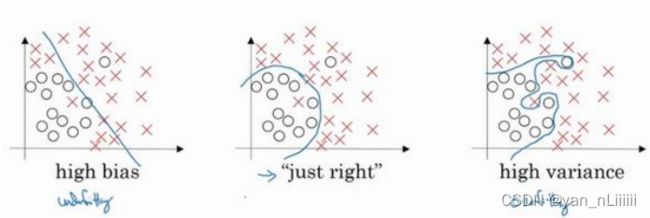
- 理解偏差和方差的两个关键数据是训练集误差(Train set error)和验证集误差(Dev set error):
- 假定训练集误差是 1%,为了方便论证,假定验证集误差是 11%,可以看出训练集设置得非常好而验证集设置相对较差,我们可能过度拟合了训练集,在某种程度上验证集并没有充分利用交叉验证集的作用,像这种情况,我们称之为“高方差”;即:差的多:方差高
- 假设训练集误差是 15%,验证集误差是 16%,训练数据的拟合度不高,就是数据欠拟合,就可以说这种算法偏差比较高。即:训练集误差高-高偏差
- 再举一个例子,训练集误差是 15%,偏差相当高,但是验证集的评估结果更糟糕,错误率达到 30%,这是方差偏差都很糟糕的情况。
- 一般来说,最优误差也被称为贝叶斯误差,所以,如果最优误差或贝叶斯误差非常高,比如 15%。我们再看看这个分类器(训练误差15%,验证误差 16%),则15%的错误率对训练集来说也是非常合理的,偏差不高,方差也非常低。
针对偏差方差的优化
- 初始模型训练完成后,我首先要知道算法的偏差高不高,如果偏差较高,试着评估训练集或训练数据的性能。如果偏差的确很高,甚至无法拟合训练集,那么你要做的就是选择一个新的网络,比如含有更多隐藏层或者隐藏单元的网络。采用规模更大的网络通常都会有所帮助,延长训练时间不一定有用,但也没什么坏处。反复尝试,直到可以拟合数据为止,至少能够拟合训练集。
- 一旦偏差降低到可以接受的数值,检查一下方差有没有问题。如果方差高,解决办法:采用更多数据;正则化。
- 正则化: λ / 2 m Σ ∣ ∣ w ∣ ∣ 2 λ/2m Σ||w||^{2} λ/2mΣ∣∣w∣∣2
为什么只正则化参数而不再加上参数 呢?你也可以这么做,只是我们习惯省略不写,因为通常是一个高维参数矢量,已经可以表达高偏差问题,可能包含有很多参数,我们不可能拟合所有参数,而只是单个数字,所以几乎涵盖所有参数。
于是, λ 变成了一个需要调整的超级参数。
dropout 正则化
dropout 会遍历网络的每一层,并设置消除神经网络中节点的概率,最后得到一个节点更少,规模更小的网络。我们用一个三层( = 3)网络来举例说明:
- 首先要定义向量, [ 3 ] ^{[3]} [3]表示一个三层的 dropout 向量:
d3 = np.random.rand(a3.shape[0],a3.shape[1])
向量或 [ 3 ] ^{[3]} [3]用来决定第三层中哪些单元归零。 - 然后看它是否小于某数,我们称之为 keep-prob。keep-prob 是一个具体数字,它表示保留某个隐藏单元的概率,此处 keep-prob 等于 0.8,它的作用就是生成随机矩阵,其中 [ 3 ] ^{[3]} [3]中的对应值为 1 的概率都是 0.8,对应为 0 的概率是 0.2,随机数字小于 0.8。它等于 1 的概率是 0.8,等于 0 的概率是 0.2。
- 接下来要做的就是从第三层中获取激活函数,这里我们叫它 [ 3 ] ^{[3]} [3], [ 3 ] ^{[3]} [3]等于上面的 [ 3 ] ^{[3]} [3]乘以 [ 3 ] ^{[3]} [3],
a3 =np.multiply(a3,d3),也可写3 ∗= 3,它的作用就是让 [ 3 ] ^{[3]} [3]中各个元素等于 0 的概率为20%。 - 最后,我们向外扩展[3],用它除以除以 keep-prob 参数:
3/= − b,原因: [ 4 ] ^{[4]} [4]= [ 4 ] ^{[4]} [4] [ 3 ] ^{[3]} [3]+ [ 4 ] ^{[4]} [4],为了不影响z [ 4 ] ^{[4]} [4]的期望值,我们用 [ 4 ] ^{[4]} [4]a [ 3 ] ^{[3]} [3]/0.8,会修正我们所需的那20%。这一步骤就是所谓的dropout法。反向随机失活(inverted dropout)方法通过除以 keep-prob,确保 [ 3 ] ^{[3]} [3]的期望值不变。,目前实施 dropout 最常用的方法就是 Inverted dropout
通常我们在测试阶段不会使用dropout函数,我们不期望输出结果是随机的,如果测试阶段应用 dropout 函数,预测会受到干扰。
dropout 的功能类似于2正则化,与2正则化不同的是应用方式不同会带来一点点小变化,甚至更适用于不同的输入范围。对于不同的应用方式 dropout正则化的情况也会不同。
总结一下,如果你担心某些层比其它层更容易发生过拟合,可以把某些层的 keep-prob值设置得比其它层更低,缺点是为了使用交叉验证,你要搜索更多的超级参数;另一种方案 是在一些层上应用 dropout,而有些层不用dropout,应用 dropout 的层只含有一个超级参 数,就是 keep-prob。
dropout在计算机视觉中应用得比较频繁,有些计算机视觉研究人员非常喜欢用它,几乎成了默认的选择。
其他正则化方法
梯度消失/梯度爆炸
指导数或坡度有时会变得非常大,或者非小,甚至于以指数方式变大变小,这加大了训练的难度。无法完全消除,但可以通过权重初始化减缓。
- 权重初始化:
- 比如只有一个神经元的情况:
= 1 1 + 2 2 + ⋯ + , = 0 = _1_1 + _2_2 + ⋯ + __, = 0 z=w1x1+w2x2+⋯+wnxn,b=0,为了预防值过大或过小,可以看到越大,你希望越小,最合理简单的方法就是设置 = 1/,表示神经元的输入特征数量, [ ] ^{[]} [l] =. . (shape) ∗ np. sqrt(1/[−1])(tanh激活函数),[−1]是第 − 1层神经元数量。这里的1/[−1]为方差。
如果用的是 Relu 激活函数,方差设置为2/,效果会更好。 - 如果激活函数的输入特征被零均值和标准方差化,则方差是 1,也会调整到相似范围,这就降低了梯度消失和爆炸问题,因为它给权重矩阵设置了合理值,你也知道,权重不能比 1 大很多,也不能比 1 小很多。
- 比如只有一个神经元的情况:
梯度检验
- 首先,不要在训练中使用梯度检验,它只用于调试。为了实施梯度下降,必须使用和 backprop 来计算,并使backprop 来计算导数,只有调试的时候,才会用梯度检验来确认数值是否接近。完成后,关闭梯度检验。
- 如果算法的梯度检验失败,要检查所有项,检查每一项,并试着找出 bug,也就是说,如果 a p p r o x [ i ] _{approx}[i] approx[i]与[i]相差很大,我们要做的就是查找不同的值,看看是哪个导致这个差距的。
- 第三点,在实施梯度检验时,如果使用正则化,请注意正则项。等于与相关的函数的梯度,记住一定要包括正则项。
- 第四点,梯度检验不能与 dropout 同时使用,因为每次迭代过程中,dropout 会随机消除隐藏层单元的不同子集,难以计算 dropout 在梯度下降上的代价函数。建议先关闭 dropout,用梯度检验进行双重检查,因为在没有 dropout 的情况下,你的算法至少是正确的,然后打开 dropout。
优化算法
Mini-batch梯度下降
把训练集分割为小一点的子集训练,这些子集被取名为 mini-batch。
之前我们使用了上角小括号()表示训练集里的第i个训练样本,用上角中括号[]来表示神经网络的第层,现在引入大括号来代表第i个mini-batch, ^{} t和 ^{} t。
- mini-batch的大小:
设m为训练集的大小,如果 mini-batch 的大小等于,其实就是传统的 batch 梯度下降法;另一个极端情况,假设 mini-batch 大小为 1,就有了新的算法,叫做随机梯度下降法。
考虑到电脑内存设置和使用的方式,如果 mini-batch 大小是 2 的次方,代码会运行地快一些。64 到 512 的 mini-batch 比较常见。
指数加权平均数算法
就是一种计算平均数的算法。
作用:从计算和内存效率来说,这是一个有效的方法,所以在机器学习中会经常使用,更不用说只要一行代码,这也是一个优势。
- 例如:伦敦的每日温度图如下:
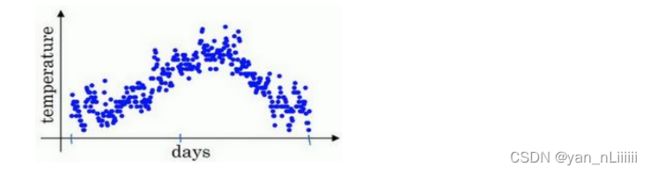
首先,使 0 = 0 _{0}=0 v0=0,然后, t = β t − 1 + ( 1 − β ) θ t _{t}=β_{t-1}+(1-β)θ_{t} vt=βvt−1+(1−β)θt,其中, θ t θ_{t} θt表示当日温度。
β=0.9:红线 每天只取0.1的权重
β=0.98接近1:绿线 每天只取0.02的权重
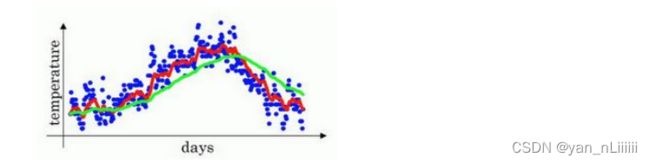
高值得到的曲线要平坦一些,原因在于多平均了几天的温度,所以这个曲线波动更小,缺点是曲线进一步右移,出现一定延迟,因为当 = 0.98,相当于给前一天的值加了太多权重,只有 0.02 的权重给了当日的值。
如果是另一个极端值0.5,相当于平均了两天的温度:
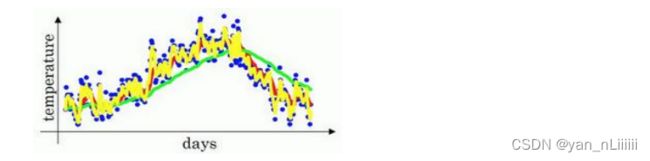
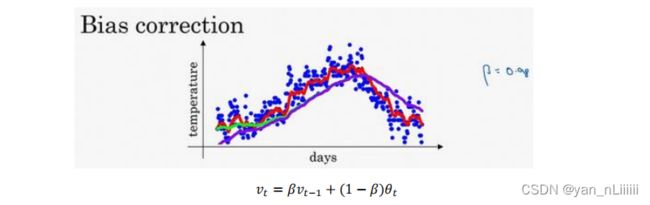
这个黄色线能更快适应温度变化。 - 偏差修正:
可以使平均数运算更加准确
方法:不用 t _{t} vt,而是用 t / ( 1 − β t ) _{t}/(1-β_{t}) vt/(1−βt)
可以让估测变得更好,更准确,特别是在估测初期;当很大的时候, β t β^{t} βt接近0,偏差修正几乎没有作用。如紫线:
Momentum/动量梯度下降法
简而言之,基本的想法就是计算梯度的指数加权平均数,并利用该梯度更新权重。
如图:

慢慢摆动到最小值,这种上下波动减慢了梯度下降法的速度,你就无法使用更大的学习率,如果你要用较大的学习率(紫色箭头),结果可能会偏离函数的范围。在纵轴上,你希望学习慢一点,因为你不想要这些摆动,但在横轴上,你希望加快学习,快速从左向右移,移向最小值红点。
-
做法:
d W = β d W + ( 1 − β ) d W , d b = β d b + ( 1 − β ) d b _{dW}=β_{dW}+(1-β)dW, _{db}=β_{db}+(1-β)db vdW=βvdW+(1−β)dW,vdb=βvdb+(1−β)db
这与之前的公式 t = β t − 1 + ( 1 − β ) θ t _{t}=β_{t-1}+(1-β)θ_{t} vt=βvt−1+(1−β)θt相似。 -
理解:每次都考虑所有的dW分量。当以前dW的分量都指向一个方向,那么它会叠加其它分量不是主方向。多个batch后会被减小,主方向不断增加,相当于加速。

这个算法肯定要好于没有 Momentum 的梯度下降算法,我们还可以做别的事情来加快学习算法。
RMSprop算法
root mean square prop
- 如果你想:

公式:

理解:
因为对纵轴求导和对横轴求导的小大不一样,S值就是为了使大的更大,小的更小,这样在作为分母时,就能在梯度上呈现出相反的情况,减小震荡的同时加速梯度下降。
为了确保数值稳定,在实际操练的时候,通常在分母上加上一个很小很小的,是多少没关系, 1 0 − 8 10^{−8} 10−8是个不错的选择,这只是保证数值能稳定一些。
Adam优化算法:
Adam 优化算法基本上就是将 Momentum 和 RMSprop 结合在一起。
以db为例,dW同理:
- Momentum:
d b = β 1 d b + ( 1 − β 1 ) d b _{db}=β_1_{db}+(1-β_1)db vdb=β1vdb+(1−β1)db - RMSprop:
由方差性质可知:
S d b = β 2 S d b + ( 1 − β 2 ) ( d b ) 2 S_{db}=β_2S_{db}+(1-β_2)(db)^2 Sdb=β2Sdb+(1−β2)(db)2 - 加上偏差修正:
v d b c o r r e c t e d = v d b / ( 1 − β 1 t ) v_{db}^{corrected}=v_{db}/(1-β_1^{t}) vdbcorrected=vdb/(1−β1t)
S d b c o r r e c t e d = S d b / ( 1 − β 2 t ) S_{db}^{corrected}=S_{db}/(1-β_2^{t}) Sdbcorrected=Sdb/(1−β2t)
- 1常用的缺省值为 0.9,至于超参数2,Adam 算法的发明者推荐使用 0.999,关于的选择其实没那么重要,Adam 作者建议为10^(−8),但你并不需要设置它,因为它并不会影响算法表现。
学习率衰减
慢慢减少的本质在于:在学习初期,你能承受较大的步伐,但当开始收敛的时候,小一些的学习率能让你步伐小一些。
拆分成不同的 mini-batch,第一次遍历训练集叫做第一代,第二次就是第二代。epoch-num表示第几代:

例子:

我们要做的是要去尝试不同的值,包括超参数0,以及超参数衰退率,找到合适的值。
还有很多衰减,如:指数衰减、离散下降、手动衰减等。
超参数调试
学习率a调试
- 在早一代的机器学习算法中,如果你有两个超参数:超参 1,超参 2,常见的做法是在网格中取样点。这里放置的是 5×5 的网格,你可以尝试这所有的 25 个点,然后选择哪个参数效果最好。当参数的数量相对较少时,这个方法很实用;
在深度学习领域,我们常做的是随机选择点,如左图所示:
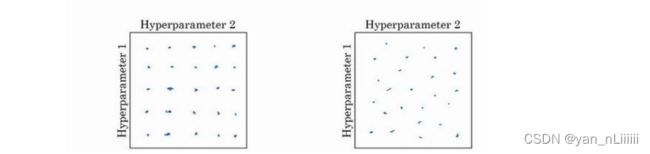
若三个超参数:立方体 - 另一个惯例是采用由粗糙到精细的策略:
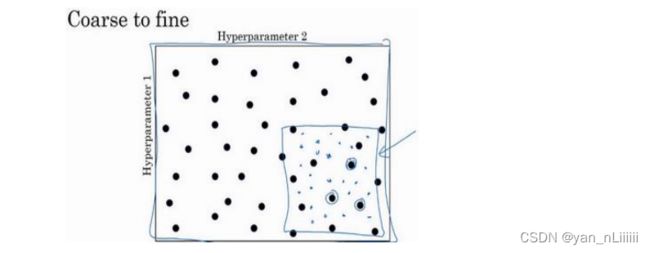
为超参数选择合适的范围-a和β
a:
用对数标尺搜索超参数的方式会更合理,通常不使用线性轴,分别依次取0.0001,0.001,0.01,0.1,1,在对数轴上均匀随机取点,这样,比如在
0.0001 到 0.001 之间,就会有更多的搜索资源可用。
- 取最小值的对数为a,最大值的对数为b
- r在对数轴上的10^ 到 10^ 区间取值
- 将超参数设置为10^ r
- 例如:0.0001到1:
log0.0001=-4=a,log1=0=b,r=-4*np.random.rand(),然后a随机取值:a=10^r,则a∈[10^{-4},10^{0}]
β:
假设你认为是 0.9到 0.999 之间的某个值,那就不能用线性轴取值了,所以考虑这个问题最好的方法就是,我们探究1 − ,此值在0.1 到 0.001 区间内。
这里,左边的是最大值,右边的是最小值,在[−3, −1]里随机均匀给 r 取值。设定1 − = 10,所以 = 1 − 10,这就变成了在特定的选择范围内超参数随机取值。希望用这种方式得到想要的结果: 在 0.9 到 0.99 区间探究的资源,和在 0.99 到 0.999 区间探究的一样多。
注意:当接近 1 时,就会对细微的变化变得很敏感。所以在 接近 1 的区间内的取值过程中,需要更加密集地取值。
两种超参数调试方式:
Pandas and Caviar 熊猫方式和鱼子酱方式
Pandas:
观察它的表现,耐心地调试学习率,但那通常这是你没有足够的计算能力,不能在同一时间试验大量模型时才采取的办法。
Caviar:
同时试验多种模型。
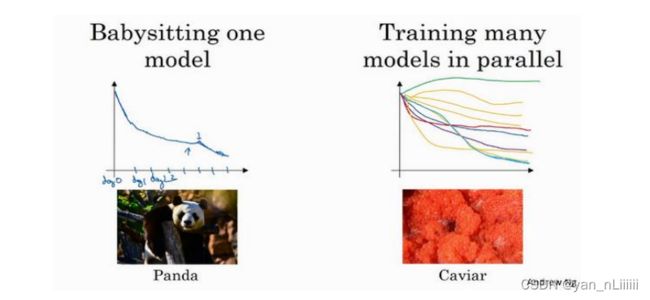
打个比方,把左边的方法称为熊猫方式。当熊猫有了孩子,他们的孩子非常少,一次通常只有一个,然后他们花费很多精力抚养熊猫宝宝以确保其能成活,所以,这的确是一种照料,一种模型类似于一只熊猫宝宝;
对比而言,右边的方式更像鱼类的行为,称之为鱼子酱方式。不对其中任何一个多加照料,只是希望其中一个,或其中一群,能够表现出色。
将称之为熊猫方式与鱼子酱方式。
Batch正则化和程序框架
Batch正则化:
简称BN
把z标准化:

其中, Z n o r m Z_{norm} Znorm=(z-μ)/(σ2+)0.5

将 Batch Norm 拟合进神经网络
BN:全称Batch Normalization(批规范化)
Batch 归一化的做法是将值进行 Batch 归一化,简称 BN,此过程将由和两参数控制,这一操作会给你一个新的规范化的值(̃[1]),然后将其输入激活函数中得到:= (̃)。
需要强调的是 Batch 归一化是发生在计算和之间的。实践中,Batch 归一化通常和训练集的 mini-batch一起使用,在每个 mini-batch上使用。
注意:在BN中,无论[]的值是多少,都是要被减去的,因为在 Batch 归一化的过程中,要减去平均值,加常数会抵消。

Batch Norm 奏效的原因总结
保证了均值和方差固定不变;
可以这样想,它减弱了前层参数的作用与后层参数的作用之间的联系,它使得网络每层都可以自己学习,稍稍独立于其它层,这有助于加速整个网络的学习;
打个比方,各种颜色的猫平均一下结果是黑猫,然后再输入到分类器,这样猫的颜色对分类的影响就可以减弱;
有轻微正则化的效果:归一化过程中,均值和方差的估计是不准确的,因此它们引来了噪声。但这噪声也实现了轻微正则化的效果,弄巧成拙了。
训练和测试时的 BN
- 在训练时,和2是在整个 mini-batch 上计算出来的,包含了一定数量的样本;
- 在测试时,是根据训练集估算和2。估算的方式有很多种,理论上可以在最终的网络中运行整个训练集来得到和2,但在实际操作中,我们通常运用指数加权平均来追踪在训练过程中看到的和2的值。然后在测试中使用和2的值来进行所需要的隐藏单元值的调整。
简单来说就是在测试test时对于单个样本均值和方差都没有意义,那么要利用训练时的数据来得到miu和sigma从而计算测试时的z_norm。
softmax回归
多种分类,不只是识别两个分类。
假设一共有四个类别:
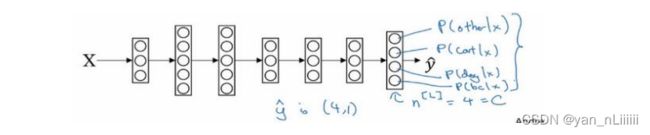
算出了之后,分为三个步骤。需要应用 Softmax 激活函数,设定一个临时变量 t = e z [ l ] t=e^{z^{[l]}} t=ez[l],并进行归一化。具体例子如下:

例如这里的第一个节点,归一化后它会输出0.842,这样说来,对于这张图片(对于这个z值),类0的概率就为84.2%,同理可得类1、类2、类3的概率,四个概率总和为1。
soft激活函数:设 [ ] ^{[]} [l]= [ ] ^{[]} [l]( [ ] ^{[]} [l]),这一激活函数
的特殊之处在于,,因为需要将所有可能的输出归一化,就需要输入一个 4×1 维向量,然后输出一个 4×1 维向量。