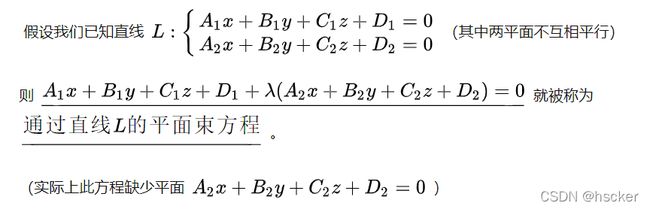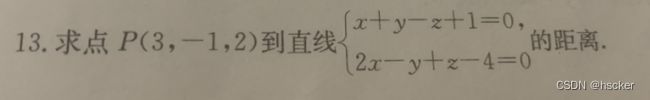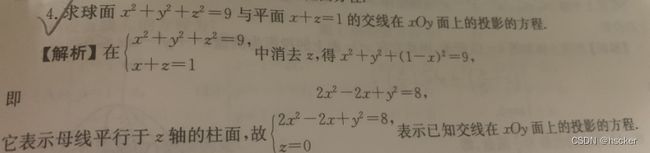空间解析几何与向量代数
一、向量基础知识
2、方向角:向量与各坐标轴的夹角
方向余弦:方向角的余弦值,即各轴对应坐标除以模长,各轴坐标即为向量的各轴投影
二、内外积与混合积
1、向量积满足反交换律,计算使用三阶行列式(行列式三行的顺序不影响计算结果)
2、证明三向量a,b,c共面,即证明三向量混合积为0
三、平面及其方程
1、平面方程有一般式(通过平面法向量确定x,y,z的系数,最后代入点求出常数D),点法式,截距式,一般式中x,y,z的系数即为平面的一个法向量
2、平面平行与哪个坐标轴,或包含,那么他的法向量对应轴坐标必为0(法向量垂直平面内任一直线),所以设方程时可以忽略掉对应变量或设法向量对应轴坐标为0,如果包含轴则平面方程不含D(因为平面过原点)
3、两平面的夹角公式即利用两个法向量的乘积求
4、求平面方程可以利用混合积(一般条件为点多,向量多)
5、点到平面的距离公式类比平面中点到直线距离公式
四、空间直线及其方程
1、一般方程(即两平面决定一条直线)
点向式方程(一定点一方向向量,式子中的方向向量代表的是过原点的一个向量,所以省略减0不写)
参数方程(令点向式等于t得到)
3、两平面的交线的方向向量可以用两平面的法向量的向量积表示
4、平面束方程:此方程表示过一条直线的所有平面(代入点来求出![]() 得到所需平面,有平面过直线的条件才设)
得到所需平面,有平面过直线的条件才设)
同理,点向式可以利用等式硬凑出含x,y,z的等式,左右随机一方乘以![]() 来设立平面束方程
来设立平面束方程
用法:题目给出过一点定直线和定点求平面时,将点代入含![]() 的方程求出后,即使所求的平面方程
的方程求出后,即使所求的平面方程
四.(1)直线,平面,定点间的关系
5、直线与平面交点问题:将直线点向式方程转为参数方程(一般式就利用三元一次方程组计算),将含t的式子代入平面方程求出t后,回代入x,y,z中即求出交点
6、定点与直线的距离问题:求出垂直于直线且过定点的平面,然后用四.5的方法联立平面与直线求出交点,最后利用两点间距离公式求出两点间距离
7、求直线在定平面上的投影直线:利用平面束方程设直线的平面,利用两平面法向量的乘积为0求出垂直平面,最后用一般式(即两平面方程组)表示投影直线
8、两直线相交用已知直线求未知直线问题:利用混合积结果等于0,第一行表示为过定点的向量,二三行分别为两个直线的方向向量(只要三个向量都是共面的,都可以用这个混合积令其等于0来求解未知数)(此方法也可看做求平面,二三行的向量积是法向量,第一行是定点,即点法式方程)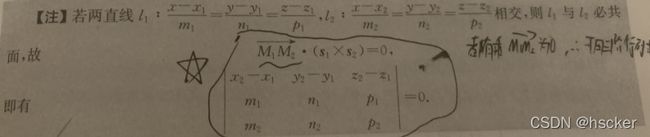
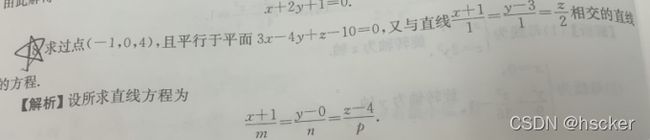 9、三维空间中点到直线的距离:求p到直线l的距离,设p0为直线上任意一点,直线方向向量为s,距离d=
9、三维空间中点到直线的距离:求p到直线l的距离,设p0为直线上任意一点,直线方向向量为s,距离d=
点到平面的距离:p0(x0,y0,z0),平面Ax+By+Cd+D=0,d=![]() (即二维平面中点到直线的进阶版)
(即二维平面中点到直线的进阶版)
10、一点一直线求平面方程:同8的方法一样,利用混合积等到结果为0的方程式
11、两直线间的距离公式:设两直线方向向量为s1,s2,A,B分别为两线上的点,d=![\frac{\left [ s1s2\vec{AB} \right ]}{\left | s1\times s2 \right |}](http://img.e-com-net.com/image/info8/61a386771fab474380aa7ae383caad06.gif)

五、曲面及其方程
(1)柱面
由一条准线上各个点沿着母线方向不断平移延伸而形成的曲面,方程式多为只含x,y的方程,这样不含z就可以沿着z轴方向不断平移延伸形成柱面
(2)旋转曲面
某平面的曲线绕着此面内的一个定轴旋转而形成的曲面,绕哪个轴哪个变量不变,而因为曲面必有z,所以另一个变量会加上z(例如绕y转,那么x会变为![]() )
)
例1、求旋转曲面![]() 如何形成
如何形成
(3)二次曲面
1、椭圆锥面、椭圆抛物面、双曲抛物面区别:前者z有平方,中后者z为一次方,中者x,y系数为正,后者x,y系数一正一负(即符合平面的椭圆与双曲线形式)
单双叶双曲面区别:单叶为一,双叶为负一,同化为1,双叶的负系数更多
椭球面即在三个面内都是椭圆图形
例1(求曲线在某平面的投影)
例2 求柱面方程,x0代表准线上的点,x代表柱面上的点,后者范围更大包含了前者全部点
例3 求旋转面方程(绕着哪个轴转,哪个轴会成为曲线与曲面方程的沟通桥梁,例如绕着z轴,则有z=z0)(旋转后那一圈的点到原点的距离都一样)
六、空间曲线及其方程
只有等号代表曲面,有大于小于号代表曲面体
![\left [ abc \right ]= \begin{vmatrix} ax & ay &az \\ bx & by & bz\\ cx&cy & cz \end{vmatrix}=\left [ a\times b \right ]\cdot c](http://img.e-com-net.com/image/info8/56214e00b4794efd8adba537e428819b.gif)