关于方向导数和梯度你真的懂了吗？

前言

方向导数和梯度是多元函数微分学中两个抽象的概念，如果对它们没有深刻的理解，那么就会感觉晦涩难懂，今天我们来对二者进行一个总结。
在介绍方向导数和梯度之前，我们先回顾两个知识点：空间曲线的切线与法平面、曲面的切平面与法线。

---

一、空间曲线的切线与法平面

若空间曲线$\Gamma$的方程为
$$\{\begin{array}{l}x=\phi \left(t\right),\\ y=\psi \left(t\right),\\ z=\omega \left(t\right),\end{array}t\in \left[\alpha ,\beta \right]$$
点$M$处对应的参数为$t_0$
点$M$处的切向量为$T=\left({\phi }^{\prime }\left(t_0\right),{\psi }^{\prime }\left(t_0\right),{\omega }^{\prime }\left(t_0\right)\right)$
则曲线在点$M$处的切线方程为
$$\frac{x-x_0}{{\phi }^{\prime }\left(t_0\right)}=\frac{y-y_0}{{\psi }^{\prime }\left(t_0\right)}=\frac{z-z_0}{{\omega }^{\prime }\left(t_0\right)}$$
法平面方程为
$${\phi }^{\prime }\left(t_0\right)\left(x-x_0\right)+{\psi }^{\prime }\left(t_0\right)\left(y-y_0\right)+{\omega }^{\prime }\left(t_0\right)\left(z-z_0\right)=0$$

若空间曲线$\Gamma$的方程为
$$\{\begin{array}{l}y=\phi \left(x\right)\\ z=\psi \left(x\right)\end{array}$$
我们取$x$为参数，则方程可以表示为
$$\{\begin{array}{l}x=x\\ y=\phi \left(x\right)\\ z=\psi \left(x\right)\end{array}$$
点$M$处对应的参数为$x_0$
点$M$处的切向量为$T=\left(1,{\phi }^{\prime }\left(x_0\right),{\psi }^{\prime }\left(x_0\right)\right)$
则曲线在点$M$处的切线方程为
$$\frac{x-x_0}{1}=\frac{y-y_0}{{\phi }^{\prime }\left(x_0\right)}=\frac{z-z_0}{{\psi }^{\prime }\left(x_0\right)}$$
法平面方程为
$$\left(x-x_0\right)+{\phi }^{\prime }\left(x_0\right)\left(y-y_0\right)+{\psi }^{\prime }\left(x_0\right)\left(z-z_0\right)=0$$

若空间曲线$\Gamma$的方程为
$$\{\begin{array}{l}F\left(x,y,z\right)=0\\ G\left(x,y,z\right)=0\end{array}$$即一般方程
我们可以将方程变形为
$$\{\begin{array}{l}x=x\\ F\left(x,y,z\right)=0\\ G\left(x,y,z\right)=0\end{array}$$
先利用隐函数方程组求导的知识解出$\frac{dy}{dx}$和$\frac{dz}{dx}$，我们就可以得到曲线在某点的切向量为$T=\left(\frac{dx}{dx},\frac{dy}{dx},\frac{dz}{dx}\right)$
则曲线在点$M$处的切线方程为
$$\frac{x-x_0}{\frac{dx}{dx}}=\frac{y-y_0}{\frac{dy}{dx}}=\frac{z-z_0}{\frac{dz}{dx}}$$
法平面方程为
$$\frac{dx}{dx}\left(x-x_0\right)+\frac{dy}{dx}\left(y-y_0\right)+\frac{dz}{dx}\left(z-z_0\right)=0$$

二、曲面的切平面与法线

若曲面方程为$F(x,y,z)=0$，已知曲面上一点$M(x_0，y_0,z_0)$
垂直于曲面上该点切平面的法向量为
$$n=\left(F_x\left(x_0,y_0,z_0\right),F_y\left(x_0,y_0,z_0\right),F_z\left(x_0,y_0,z_0\right)\right)$$
则点$M$处切平面的方程为
$$F_x\left(x_0,y_0,z_0\right)\left(x-x_0\right)+F_y\left(x_0,y_0,z_0\right)\left(y-y_0\right)+F_z\left(x_0,y_0,z_0\right)\left(z-z_0\right)=0$$
法线的方程为
$$\frac{x-x_0}{F_x\left(x_0,y_0,z_0\right)}=\frac{y-y_0}{F_y\left(x_0,y_0,z_0\right)}=\frac{z-z_0}{F_z\left(x_0,y_0,z_0\right)}$$

若曲面方程为$z=f(x,y)$，已知曲面上一点$M(x_0，y_0,z_0)$
令$F(x,y,z)=f(x,y)-z$
垂直于曲面上该点切平面的法向量为
$$n=\left(f_x\left(x_0,y_0\right),f_y\left(x_0,y_0\right),-1\right)$$
则点$M$处切平面的方程为
$$f_x\left(x_0,y_0\right)\left(x-x_0\right)+f_y\left(x_0,y_0\right)\left(y-y_0\right)-\left(z-z_0\right)=0$$
法线方程为
$$\frac{x-x_0}{f_x\left(x_0,y_0\right)}=\frac{y-y_0}{f_y\left(x_0,y_0\right)}=\frac{z-z_0}{-1}$$

三、方向导数和梯度

如果函数$f(x,y)$在点$P_0(x_0,y_0)$可微分，则函数在该点沿任意方向$l$的方向导数存在
$${\frac{\partial f}{\partial l}|}_{\left(x_0,y_0\right)}=f_x\left(x_0,y_0\right)\cos \alpha +f_y\left(x_0,y_0\right)\cos \beta$$
其中$cos\alpha$和$cos\beta$是方向$l$上的方向余弦。

与方向导数有关联的概念是函数的梯度，首先要强调梯度是一个向量，那么梯度是一个怎样的向量呢？接下来一起看一下：
$${\frac{\partial f}{\partial l}|}_{\left(x_0,y_0\right)}=f_x\left(x_0,y_0\right)\cos \alpha +f_y\left(x_0,y_0\right)\cos \beta$$
$$=\left(f_x\left(x_0,y_0\right),f_y\left(x_0,y_0\right)\right)\cdot \left(\cos \alpha ,\cos \beta \right)$$
$$=\nabla f\left(x_0,y_0\right)\cdot e_l$$
$$=|\nabla f\left(x_0,y_0\right)|\cos \theta$$
其中$\theta$是梯度与$l$方向的夹角
从上面我们可以得到梯度
$\nabla f\left(x_0,y_0\right)=f_x\left(x_0,y_0\right)i+f_y\left(x_0,y_0\right)j=\left(f_x\left(x_0,y_0\right),f_y\left(x_0,y_0\right)\right)$
梯度是这样一个向量：它的方向是函数在这点方向导数取最大值的方向，它的模等于方向导数的最大值

梯度的几何意义

首先要明确我们上面定义的梯度是二元函数的梯度
函数为二元函数$z=f(x,y)$时在空间中表示的是一个曲面，但是函数上某一点的梯度是二维空间中的一个向量
不少同学会在这儿感到疑惑，包括本人也是经过了思考才搞清楚的

第一个图形上有若干个等值面，它们在$xOy$平面内的投影即为第二个图形
譬如函数上$H$点的梯度方向如图所示，我们发现二元函数上某一点的梯度方向就是二维平面内的一个向量(注意：梯度方向为等值线上垂直于该点切线的法线方向)

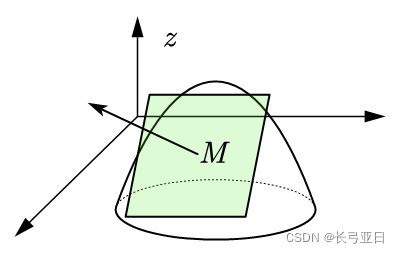
如果函数是一个三元函数$u=f(x,y,z)$，它的图形是一个超曲面，在三维空间我们无法绘制出来，但是它的投影却是三维空间的曲面，称之为等值面，我们可以绘制出一个三元函数在三维空间的等值面
如图所示

譬如函数上点$M$处的梯度方向如图所示，三元函数上某一点梯度的方向就是三维空间中的一个向量(注意：梯度方向为等值面上垂直于该点切平面的法线方向)

---

总结

(一)二元函数梯度的方向就是等值线上该点的法线方向
(二)三元函数梯度方向就是等值面上该点的法线方向（该点切平面的法线方向），通常用来求曲面上某点的切平面方程和法线方程