基于matlab实现数字图像处理之图像复原
一、实验目的
(1)了解图像复原的目的及意义,加深对图像复原的感性认识。
(2)熟练掌握逆滤波、维纳滤波图像复原方法。
二、实验仪器(软件平台)
Matlab软件
三、实验原理
1. 点扩散(PSF)函数
点扩散函数(PSF)描述了一个成像系统对一个点光源(物体)的响应。PSF的一般术语就是系统响应,PSF是一个聚焦光学系统的冲击响应。在大多情况下,PSF可以认为像是一个能够表现未解析物体的图像中的一个扩展区块。
利用fspecial(type,para)函数来对图像进行点扩散来完成模糊图像,H = FSPECIAL('motion',len,theta),motion filter为运动模糊算子,有两个参数,表示摄像物体逆时针方向以theta角度运动了len个像素,len的默认值为9,theta的默认值为0。
2. 维纳滤波复原函数deconvwnr
维纳滤波一种基于最小均方误差准则、对平稳过程的最优估计器。这种滤波器的输出与期望输出之间的均方误差为最小,因此,它是一个最佳滤波系统。它可用于提取被平稳噪声污染的信号。从连续的(或离散的)输入数据中滤除噪声和干扰以提取有用信息的过程称为滤波,这是信号处理中经常采用的主要方法之一,具有十分重要的应用价值,而相应的装置称为滤波器。
维纳滤波是有约束的图像恢复方法,需要注意图像的噪信比(NSR),或者噪声自相关(NCORR)和图像自相关(ICORR)。
四、实验内容
1.用点扩散(PSF)函数创建运动模糊图像,修改参数改变模糊程度。
a) 无噪声运动模糊图像
b) 有噪声运动模糊图像
2.用维纳滤波复原函数deconvwnr 对模糊图像进行复原重建。
a) 对无噪声运动模糊图像用deconvwnr(I,PSF)进行复原;
b) 对有噪声运动模糊图像用deconvwnr(I,PSF)、deconvwnr(I,PSF,NSR) 和deconvwnr(I,PSF,NCORR,ICORR)函数进行复原。
c) 在实际应用过程中,常常无法准确得知噪声图像和理想图像的功率谱,试着用常数K来代替NSR,并通过实验观察不同K对图像复原效果的影响。
clc;clear;%A(m:n):取A矩阵中第m行第n列的值;A(:):把A矩阵转为列向量
R = imread('x.jpg');
%设置模糊滤波器
PSF = fspecial('motion',50,20);
%生成模糊滤波后的图片,卷积,二维展开
fr1 = imfilter(R,PSF,'conv','circular');%无噪声模糊图片
R1 = deconvwnr(fr1,PSF);
figure(1);
subplot(131);imshow(R,[]);title('原始图像');
subplot(132);imshow(fr1,[]);title('无噪声模糊图像');
subplot(133);imshow(R1,[]);title('逆滤波复原图像');
% randn(511,1)函数用来产生511个正态分布随机噪声
noise = randn(size(R));%生成正态随机噪声 %0.05* NSR=0.0164; 1* 6.5339
fr2 = im2double(fr1) +noise;%生成带正态加性噪声的模糊图像;注意noise是double类型,fr1是uint8类型
R2 = deconvwnr(fr1,PSF);
%NSR-信噪比
NSR = sum(abs(noise(:)).^2)/sum(abs(im2double(R(:))).^2);%需是二维的,现在R和noise是三维的,用(:)减少一个维度,用sum来限制数组大小
R3 = deconvwnr(fr2,PSF,NSR);
%自相关-功率谱的傅里叶变换,功率谱-信号的频谱的绝对值的平方
%NCORR-噪声自相关;ICORR-图像自相关
NCORR = real(ifft2((abs(fft2(noise)).^2)));
ICORR = real(ifft2((abs(fft2(im2double(R))).^2)));
R4 = deconvwnr(fr2,PSF,NCORR,ICORR);%自相关要取实部
figure(2);
subplot(231);imshow(R,[]);title('原始图像');
subplot(232);imshow(fr2,[]);title('有噪声模糊图像');
subplot(233);imshow(R2,[]);title('有噪声无参数逆滤波复原图像');
subplot(234);imshow(R3,[]);title('有噪声信噪比逆复原图像');
subplot(235);imshow(R4,[]);title('有噪声自相关逆复原图像');
%自定义K代替NSR
RR1 = deconvwnr(fr2,PSF,1);
RR2 = deconvwnr(fr2,PSF,0.5);
RR3 = deconvwnr(fr2,PSF,0.1);
RR4 = deconvwnr(fr2,PSF,0.05);
RR5 = deconvwnr(fr2,PSF,0.01);
RR6 = deconvwnr(fr2,PSF,0.005);
RR7 = deconvwnr(fr2,PSF,0.001);
figure(3);
subplot(331);imshow(R3,[]);title('NSR逆复原图像');
subplot(332);imshow(RR1,[]);title('k=1逆复原图像');
subplot(333);imshow(RR2,[]);title('k=0.5逆复原图像');
subplot(334);imshow(RR3,[]);title('k=0.1逆复原图像');
subplot(335);imshow(RR4,[]);title('k=0.05逆复原图像');
subplot(336);imshow(RR5,[]);title('k=0.01逆复原图像');
subplot(337);imshow(RR6,[]);title('k=0.005逆复原图像');
subplot(338);imshow(RR7,[]);title('k=0.001逆复原图像');
[实验结果]
| 图 6无噪模糊图像复原结果 |
图 7 有噪模糊图像三种复原结果 |
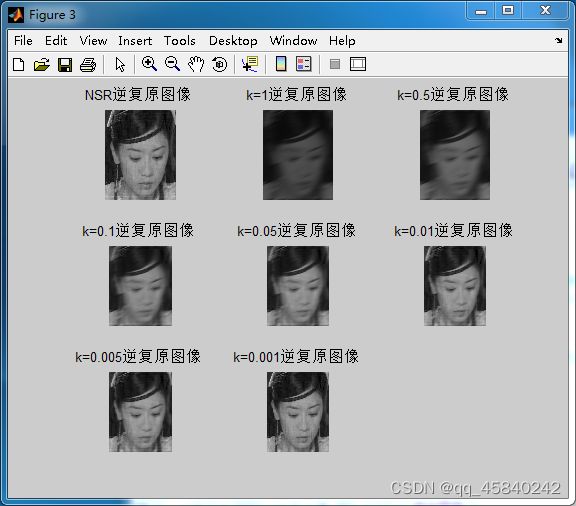
图 8 不同K值对复原效果的影响
采用仿真的方法对清晰的图像加以运动模糊,形成模糊的图像。用这种模型来描述由于目标或摄像头运动,而导致的图像模糊。 同时在加入正态分布的随机噪声图像显得更加灰暗。
由实验结果可以看出,当图像无噪声或噪声较小,即轻度降质时,采用逆滤波恢复的方法可以获得较好的结果。
比较复原结果可以发现,在对图像和噪声信息都未知的情况下采用不带参数的维纳滤波(逆滤波)形式进行复原效果很不好,在已知信噪比NSR参数的情况的维纳滤波复原效果有了较大的改善,在已知噪声和原图像的自相关函数等参数的情况下的维纳滤波复原效果最佳。
实验中NSR取均值时为0.0164,在[0.1,0.05]之间。由实验结果可知,在带噪信比参数的维纳滤波复原中,当NSR取均值时滤波效果是最好的,随着滤波中NSB由均值减小时,图像的模糊运动减小但同时噪声增强了;反之,当NSB由均值增大时,图像的模糊运动增强噪声减小了。
实验心得
本次实验中添加的正态分步噪声要注意压制噪声的大小,不然噪声太大,维纳滤波是比较难以恢复图像的,会出现修复的图像大部分被黑色覆盖的问题。另外需要注意本次实验中图像是uint8类型,噪声是double类型,必要的时候需要使用im2double或im2uint8函数来进行转换。还有噪信比、噪声自相关和图像自相关的计算,自相关函数是功率频谱的傅里叶逆变换,且需要去实部real()。
在本次实验中,发现在低版本中彩色图像需要转换成灰度图像才能顺利进行,而在高版本则没有这个顾虑。
本次实验收获非常大,学会了利用fspecial()函数构建滤波器,再通过imfilter()函数进行滤波得到滤波后的图像,最后使用deconvwnr ()函数进行维纳滤波或逆滤波来恢复图像。