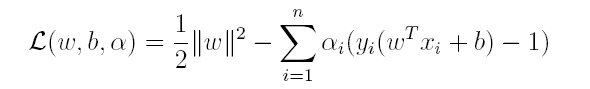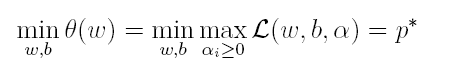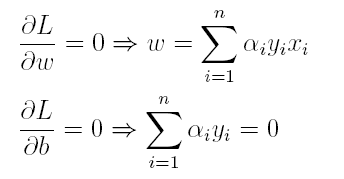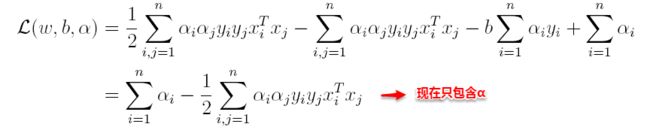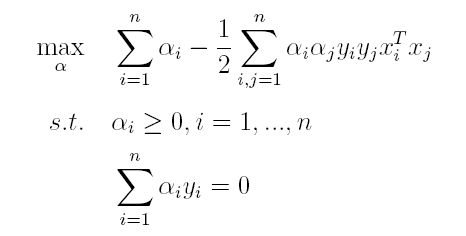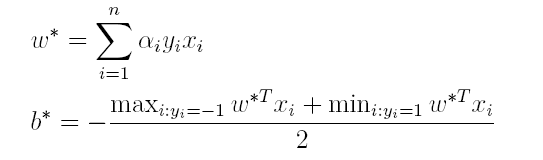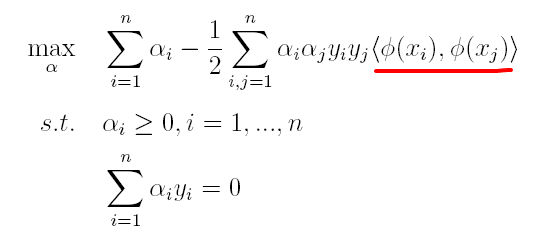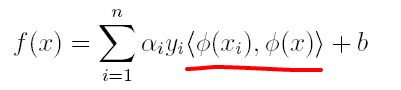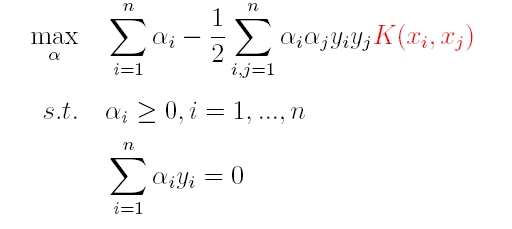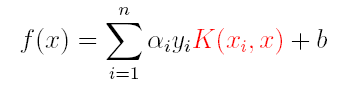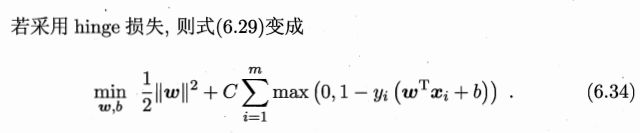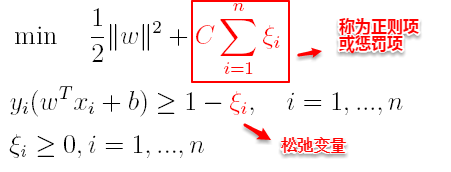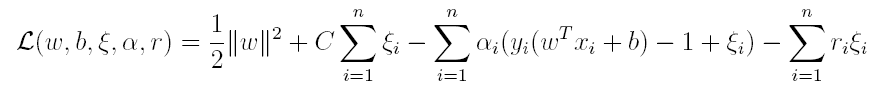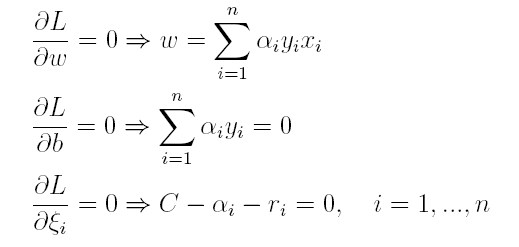【周志华机器学习】六、支持向量机
文章目录
- 参考资料
- 前言:一个关于SVM的童话故事
- 1. 基本概念
-
- 1.1 函数间隔与几何间隔
-
- 1.1.1 函数间隔
- 1.1.2 几何间隔
- 1.2 最大间隔与支持向量
- 1.3 从原始优化问题到对偶问题
- 2. 核函数
- 3. 软间隔支持向量机
- 4. SVM的一些问题
- 5. LR(逻辑回归)和SVM的联系与区别
-
- 5.1 相同点
- 5.2 不同点
- 6. 线性分类器与非线性分类器的区别以及优劣
参考资料
- Machine-learning-learning-notes
- LeeML-Notes
- ML-NLP
本博客为作者根据周志华的西瓜书和参考资料1、2、3所做的笔记,主要用于学习,非技术类博客,因此存在大量复制粘贴,请见谅。
如果本篇博客有后记部分,则该部分表示的是在书本原有的基础知识上,进行的知识点的扩充。
代码演示部分可参考github仓库。
前言:一个关于SVM的童话故事
传说魔鬼和天使玩了一个游戏,魔鬼在桌上放了两种颜色的球。魔鬼让天使用一根木棍将它们分开。这对天使来说,似乎太容易了。天使不假思索地一摆,便完成了任务。魔鬼又加入了更多的球。随着球的增多,似乎有的球不能再被原来的木棍正确分开,如下图所示。

SVM实际上是在为天使找到木棒的最佳放置位置,使得两边的球都离分隔它们的木棒足够远。依照SVM为天使选择的木棒位置,魔鬼即使按刚才的方式继续加入新球,木棒也能很好地将两类不同的球分开。
看到天使已经很好地解决了用木棒线性分球的问题,魔鬼又给了天使一个新的挑战,如下图所示。

按照这种球的摆法,世界上貌似没有一根木棒可以将它们 完美分开。但天使毕竟有法力,他一拍桌子,便让这些球飞到了空中,然后凭借 念力抓起一张纸片,插在了两类球的中间。从魔鬼的角度看这些 球,则像是被一条曲线完美的切开了。
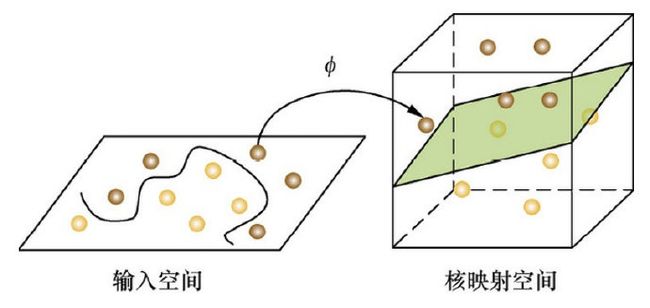
后来,“无聊”的科学家们把这些球称为“数据”,把木棍称为“分类面”,找到最 大间隔的木棒位置的过程称为“优化”,拍桌子让球飞到空中的念力叫“核映射”,在 空中分隔球的纸片称为“分类超平面”。这便是SVM的童话故事。
1. 基本概念
支持向量机(support vector machine)是一种经典的二分类模型,基本模型定义为特征空间中最大间隔的线性分类器,其学习的优化目标便是间隔最大化,因此支持向量机本身可以转化为一个凸二次规划求解的问题。
1.1 函数间隔与几何间隔
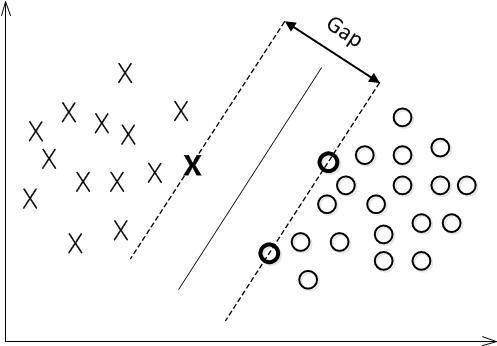
对于二分类学习,假设现在的数据是线性可分的,这时分类学习最基本的想法就是找到一个合适的超平面,该超平面能够将不同类别的样本分开,类似二维平面使用 a x + b y + c = 0 ax+by+c=0 ax+by+c=0来表示,超平面实际上表示的就是高维的平面,如下图所示:
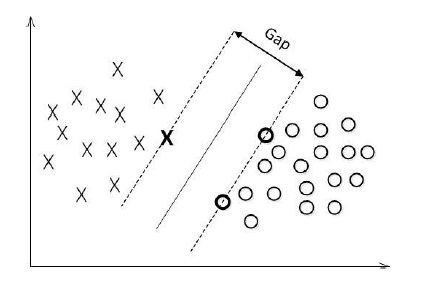
对数据点进行划分时,易知:当超平面距离与它最近的数据点的间隔越大,分类的鲁棒性越好,即当新的数据点加入时,超平面对这些点的适应性最强,出错的可能性最小。因此需要让所选择的超平面能够最大化这个间隔Gap(如下图所示)
常用的间隔定义有两种,一种称之为函数间隔,一种为几何间隔,下面将分别介绍这两种间隔,并对SVM为什么会选用几何间隔做了一些阐述。
1.1.1 函数间隔
在超平面 w T x + b = 0 w^Tx+b=0 wTx+b=0确定的情况下, ∣ w T x ∗ + b ∣ |w^Tx^*+b| ∣wTx∗+b∣能够代表点x*距离超平面的远近,易知:当 w T x ∗ + b > 0 w^Tx^*+b>0 wTx∗+b>0时,表示x*在超平面的一侧(正类,类标为1),而当 w T x ∗ + b < 0 w^Tx^*+b<0 wTx∗+b<0时,则表示x*在超平面的另外一侧(负类,类别为-1),因此 ( w T x ∗ + b ) y ∗ (w^Tx^*+b)y^* (wTx∗+b)y∗ 的正负性恰能表示数据点x*是否被分类正确。于是便引出了函数间隔的定义(functional margin):
而超平面(w,b)关于所有样本点(Xi,Yi)的函数间隔最小值则为超平面在训练数据集T上的函数间隔:
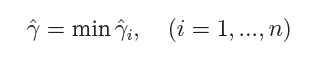
可以看出:这样定义的函数间隔在处理SVM上会有问题,当超平面的两个参数w和b同比例改变时,函数间隔也会跟着改变,但是实际上超平面还是原来的超平面,并没有变化。例如: w 1 x 1 + w 2 x 2 + w 3 x 3 + b = 0 w_1x_1+w_2x_2+w_3x_3+b=0 w1x1+w2x2+w3x3+b=0其实等价于 2 w 1 x 1 + 2 w 2 x 2 + 2 w 3 x 3 + 2 b = 0 2w_1x_1+2w_2x_2+2w_3x_3+2b=0 2w1x1+2w2x2+2w3x3+2b=0,但计算的函数间隔却翻了一倍。从而引出了能真正度量点到超平面距离的概念–几何间隔(geometrical margin)。
1.1.2 几何间隔
参考博客:https://blog.csdn.net/v_july_v/article/details/7624837
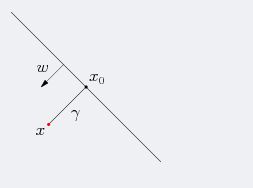
几何间隔代表的则是数据点到超平面的真实距离,对于超平面 w T x + b = 0 w^Tx+b=0 wTx+b=0, w w w代表的是该超平面的法向量,设 x 0 x_0 x0为超平面外一点x在法向量w方向上的投影点,x与超平面的距离为 γ \gamma γ,则有 x 0 = x − γ w ∣ ∣ w ∣ ∣ x_0=x-\gamma\frac{w}{||w||} x0=x−γ∣∣w∣∣w,又 x 0 x_0 x0在超平面上,即 w T x 0 = − b w^Tx_0=-b wTx0=−b,两边同乘以 w T w^T wT,代入即可得:
为了得到 γ \gamma γ的绝对值,令 γ \gamma γ乘上其对应的类别y,即可得到几何间隔的定义:
从上述函数间隔与几何间隔的定义可以看出:实质上函数间隔 y ( w T x + b ) = y f ( x ) y(w^Tx+b) = yf(x) y(wTx+b)=yf(x)就是 ∣ w T x + b ∣ |w^Tx+b| ∣wTx+b∣,而几何间隔就是点到超平面的距离。
1.2 最大间隔与支持向量
对一个数据点进行分类,当超平面离数据点的“间隔”越大,分类的确信度(confidence)也越大。所以,为了使得分类的确信度尽量高,需要让所选择的超平面能够最大化这个“间隔”值。这个间隔就是下图中的Gap的一半。
通过前面的分析可知:函数间隔不适合用来最大化间隔,因此这里我们要找的最大间隔指的是几何间隔,于是最大间隔分类器的目标函数定义为:
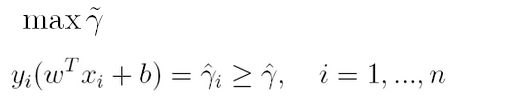
一般地,我们令 γ ^ \hat{\gamma} γ^为1(这样做的目的是为了方便推导和目标函数的优化),从而上述目标函数转化为:
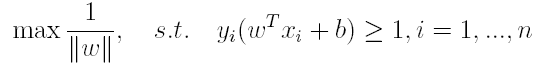
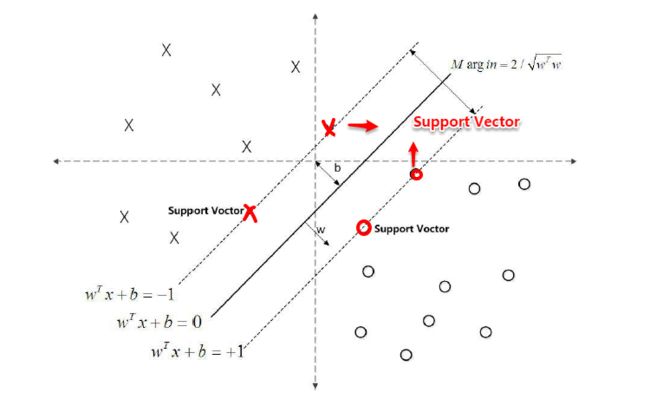
对 y ( w T x + b ) = 1 y(w^Tx+b)=1 y(wTx+b)=1的数据点,即下图中位于 w T x + b = 1 w^Tx+b=1 wTx+b=1或 w T x + b = − 1 w^Tx+b=-1 wTx+b=−1上的数据点,我们称之为支持向量(support vector),易知:对于所有的支持向量,它们恰好满足 y ( w T x + b ) = 1 y(w^Tx+b)=1 y(wTx+b)=1,而所有不是支持向量的点,有 y ( w T x + b ) > 1 y(w^Tx+b)>1 y(wTx+b)>1。
1.3 从原始优化问题到对偶问题
对于上述得到的目标函数,求 1 / ∣ ∣ w ∣ ∣ 1/||w|| 1/∣∣w∣∣的最大值相当于求 ∣ ∣ w ∣ ∣ 2 ||w||^2 ∣∣w∣∣2的最小值,因此很容易将原来的目标函数转化为:
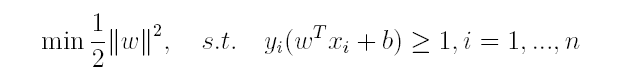
即变为了一个带约束的凸二次规划问题,可以使用现成的优化计算包(QP优化包)求解,但由于SVM的特殊性,一般我们将原问题变换为它的对偶问题,接着再对其对偶问题进行求解。
为什么通过对偶问题进行求解,有下面两个原因:
- 一是因为使用对偶问题更容易求解;
- 二是因为通过对偶问题求解出现了向量内积的形式,从而能更加自然地引出核函数。
对偶问题,顾名思义,可以理解成优化等价的问题,更一般地,是将一个原始目标函数的最小化转化为它的对偶函数最大化的问题。对于当前的优化问题,首先我们写出它的拉格朗日函数:
上式很容易验证:当其中有一个约束条件不满足时,L的最大值为 ∞(只需令其对应的α为 ∞即可);当所有约束条件都满足时,L的最大值为 1 / 2 ∣ ∣ w ∣ ∣ 2 1/2||w||^2 1/2∣∣w∣∣2(此时令所有的α为0),因此实际上原问题等价于:
由于这个的求解问题不好做,因此一般我们将最小和最大的位置交换一下(需满足KKT条件) ,变成原问题的对偶问题:
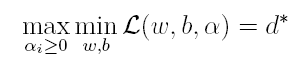
这样就将原问题的求最小变成了对偶问题求最大(用对偶这个词还是很形象),接下来便可以先求L对w和b的极小,再求L对α的极大。
(1)首先求L对w和b的极小,分别求L关于w和b的偏导,可以得出:
将上述结果代入L得到:
(2)接着L关于α极大求解α(通过SMO算法(序列最小优化算法(Sequential Minimal Optimization, SMO))求解)。
(3)最后便可以根据求解出的α,计算出w和b,从而得到分类超平面函数。
在对新的点进行预测时,实际上就是将数据点x*代入分类函数 f ( x ) = w T x + b f(x)=w^Tx+b f(x)=wTx+b中,若f(x)>0,则为正类,f(x)<0,则为负类,根据前面推导得出的w与b,分类函数如下所示,此时便出现了上面所提到的内积形式。
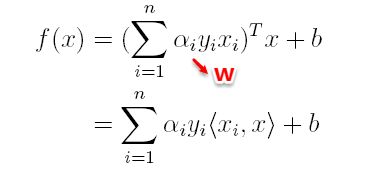
这里实际上只需计算新样本与支持向量的内积,因为对于非支持向量的数据点,其对应的拉格朗日乘子一定为0,根据最优化理论(KKT条件),对于不等式约束 ( w T x + b ) − 1 ≥ 0 (w^Tx+b)-1≥0 (wTx+b)−1≥0,满足:
2. 核函数
由于上述的超平面只能解决线性可分的问题,对于线性不可分的问题,例如:异或问题,我们需要使用核函数将其进行推广。
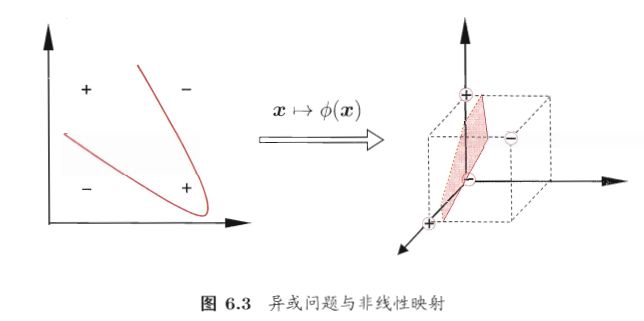
一般地,解决线性不可分问题时,常常采用映射的方式,将低维原始空间映射到高维特征空间,使得数据集在高维空间中变得线性可分,从而再使用线性学习器分类。
如果原始空间为有限维,即属性数有限,那么总是存在一个高维特征空间使得样本线性可分。若∅代表一个映射,则在特征空间中的划分函数变为:
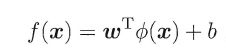
按照同样的方法,先写出新目标函数的拉格朗日函数,接着写出其对偶问题,求L关于w和b的极大,最后运用SMO算法求解α。可以得出:
(1)原对偶问题变为:
求解的过程中,只涉及到了高维特征空间中的内积运算,由于特征空间的维数可能会非常大,例如:若原始空间为二维,映射后的特征空间为5维,若原始空间为三维,映射后的特征空间将是19维,之后甚至可能出现无穷维,根本无法进行内积运算了,此时便引出了核函数(Kernel)的概念。
 因此,核函数可以直接计算隐式映射到高维特征空间后的向量内积,而不需要显式地写出映射后的结果,它虽然完成了将特征从低维到高维的转换,但最终却是在低维空间中完成向量内积计算,与高维特征空间中的计算等效(低维计算,高维表现),从而避免了直接在高维空间无法计算的问题。引入核函数后,原来的对偶问题与分类函数则变为:
因此,核函数可以直接计算隐式映射到高维特征空间后的向量内积,而不需要显式地写出映射后的结果,它虽然完成了将特征从低维到高维的转换,但最终却是在低维空间中完成向量内积计算,与高维特征空间中的计算等效(低维计算,高维表现),从而避免了直接在高维空间无法计算的问题。引入核函数后,原来的对偶问题与分类函数则变为:
(1)对偶问题:
(2)分类函数:
因此,在线性不可分问题中,核函数的选择成了支持向量机的最大变数,若选择了不合适的核函数,则意味着将样本映射到了一个不合适的特征空间,则极可能导致性能不佳。同时,核函数需要满足以下这个必要条件:
定理6.1表明,只要一个对称函数所对应的核矩阵半正定,它就能作为核函数使用,事实上,对于一个半正定核矩阵,总能找到一个与之对应的映射中.换言之,任何一个核函数都隐式地定义了一个称为“再生核希尔伯特空间”(Reproducing Kernel Hilbert Space,简称RKHS)的特征空间。
由于核函数的构造十分困难,通常我们都是从一些常用的核函数中选择,下面列出了几种常用的核函数:

3. 软间隔支持向量机
前面的讨论中,我们主要解决了两个问题:当数据线性可分时,直接使用最大间隔的超平面划分;当数据线性不可分时,则通过核函数将数据映射到高维特征空间,使之线性可分。然而在现实问题中,对于某些情形还是很难处理,例如数据中有噪声的情形,噪声数据(outlier)本身就偏离了正常位置,但是在前面的SVM模型中,我们要求所有的样本数据都必须满足约束,如果不要这些噪声数据还好,当加入这些outlier后导致划分超平面被挤歪了,如下图所示,对支持向量机的泛化性能造成很大的影响。
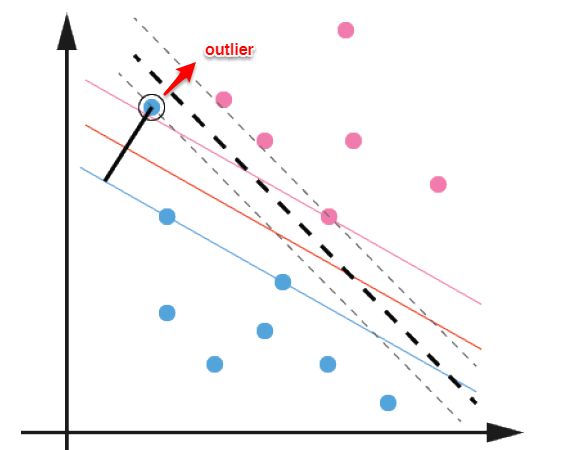
为了解决这一问题,我们需要允许某一些数据点不满足约束,即可以在一定程度上偏移超平面,同时使得不满足约束的数据点尽可能少,这便引出了软间隔支持向量机的概念
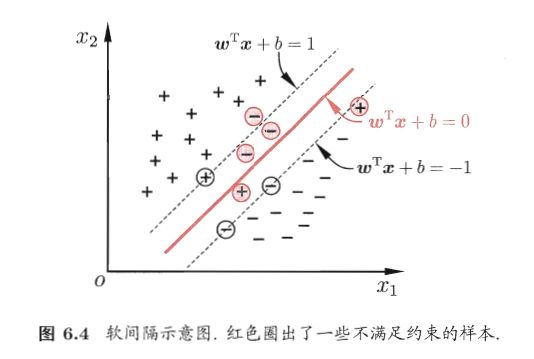
具体来说,前面介绍的支持向量机形式是要求所有样本均满足约束,即所有样本都必须划分正确,这称为硬间隔(hard margin),而软间隔则是允许某些样本不满足约束, 同时又使得不满足约束的样本尽可能少。
这样优化目标变为:
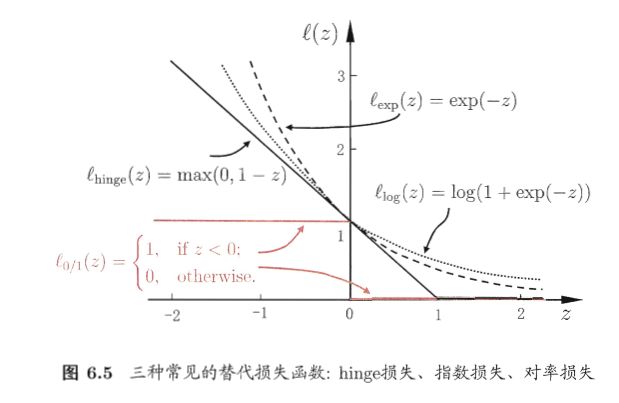
如同阶跃函数,0/1损失函数虽然表示效果最好,但是数学性质不佳。因此常用其它函数作为“替代损失函数”。

其中C为一个参数,控制着目标函数与新引入正则项之间的权重,这样显然每个样本数据都有一个对应的松弛变量,用以表示该样本不满足约束的程度,将新的目标函数转化为拉格朗日函数得到:
按照与之前相同的方法,先让L求关于w,b以及松弛变量的极小,再使用SMO求出α,有:
将w代入L化简,便得到其对偶问题:
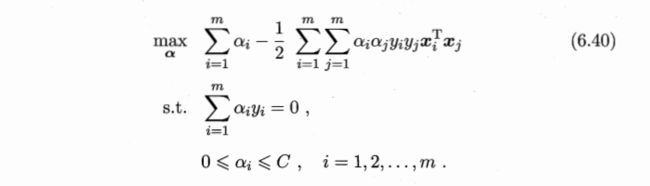
将“软间隔”下产生的对偶问题与原对偶问题对比可以发现:新的对偶问题只是约束条件中的α多出了一个上限C,其它的完全相同,因此在引入核函数处理线性不可分问题时,便能使用与“硬间隔”支持向量机完全相同的方法。
4. SVM的一些问题
-
是否存在一组参数使SVM训练误差为0?
答:存在
-
训练误差为0的SVM分类器一定存在吗?
答:一定存在
-
加入松弛变量的SVM的训练误差可以为0吗?
答:使用SMO算法训练的线性分类器并不一定能得到训练误差为0的模型。这是由 于我们的优化目标改变了,并不再是使训练误差最小。
-
带核的SVM为什么能分类非线性问题?
答:核函数的本质是两个函数的內积,通过核函数将其隐射到高维空间,在高维空间非线性问题转化为线性问题, SVM得到超平面是高维空间的线性分类平面。其分类结果也视为低维空间的非线性分类结果, 因而带核的SVM就能分类非线性问题。
-
如何选择核函数?
- 如果特征的数量大到和样本数量差不多,则选用LR或者线性核的SVM;
- 如果特征的数量小,样本的数量正常,则选用SVM+高斯核函数;
- 如果特征的数量小,而样本的数量很大,则需要手工添加一些特征从而变成第一种情况。
5. LR(逻辑回归)和SVM的联系与区别
5.1 相同点
- 都是线性分类器。本质上都是求一个最佳分类超平面。
- 都是监督学习算法。
- 都是判别模型。判别模型不关心数据是怎么生成的,它只关心信号之间的差别,然后用差别来简单对给定的一个信号进行分类。常见的判别模型有:KNN、SVM、LR,常见的生成模型有:朴素贝叶斯,隐马尔可夫模型。
5.2 不同点
-
LR是参数模型,svm是非参数模型,linear和rbf则是针对数据线性可分和不可分的区别;
-
从目标函数来看,区别在于逻辑回归采用的是logistical loss,SVM采用的是hinge loss,这两个损失函数的目的都是增加对分类影响较大的数据点的权重,减少与分类关系较小的数据点的权重
-
SVM的处理方法是只考虑support vectors,也就是和分类最相关的少数点,去学习分类器。而逻辑回归通过非线性映射,大大减小了离分类平面较远的点的权重,相对提升了与分类最相关的数据点的权重。
-
逻辑回归相对来说模型更简单,好理解,特别是大规模线性分类时比较方便。而SVM的理解和优化相对来说复杂一些,SVM转化为对偶问题后,分类只需要计算与少数几个支持向量的距离,这个在进行复杂核函数计算时优势很明显,能够大大简化模型和计算。
-
logic 能做的 svm能做,但可能在准确率上有问题,svm能做的logic有的做不了。
6. 线性分类器与非线性分类器的区别以及优劣
线性和非线性是针对模型参数和输入特征来讲的;比如输入x,模型 y = a x + a x 2 y=ax+ax^2 y=ax+ax2 那么就是非线性模型,如果输入是x和x^2则模型是线性的。
-
线性分类器可解释性好,计算复杂度较低,不足之处是模型的拟合效果相对弱些。
线性分类器包括:LR,贝叶斯分类,单层感知机、线性回归
-
非线性分类器效果拟合能力较强,不足之处是数据量不足容易过拟合、计算复杂度高、可解释性不好。
非线性分类器包括:决策树、RF、GBDT、多层感知机