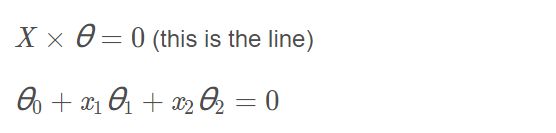吴恩达机器学习ex2:逻辑回归
吴恩达机器学习练习二：逻辑回归
1. 逻辑回归（logistic regression）
构建一个可以基于两次测试评分来评估录取可能性的分类模型。
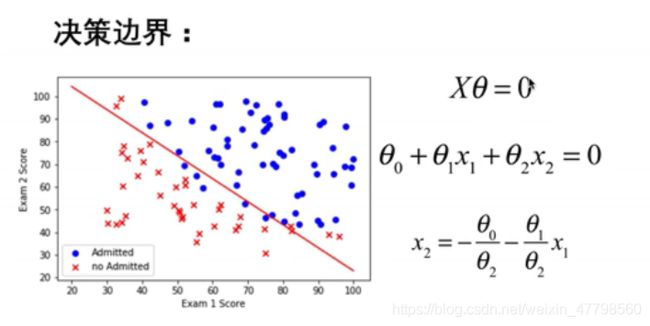
知识点回顾：
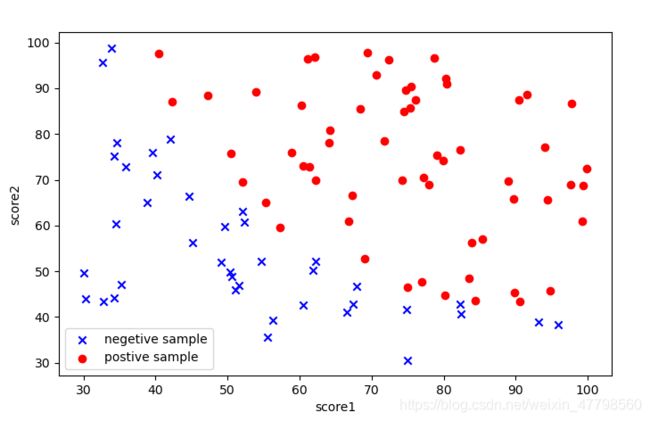
1.1 数据可视化
#coding=utf-8
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('fivethirtyeight') # 样式美化
# 读取数据，数据可视化
path = 'D:\文档\ex2data1.txt'
data = pd.read_csv(path,header= None,names = ['score1','score2','admitted'])
print(data.head())
# print(data.describe())
第一种，有点过于复杂~
# x1,y1为negetive sample; x2,y2为 postive sample
x1= []
y1 = []
x2= []
y2 = []
for i in range(data.shape[0]):
if data.iloc[i,2] == 0:
x1.append(data.iloc[i,0])
y1.append(data.iloc[i,1])
else:
x2.append(data.iloc[i,0])
y2.append(data.iloc[i, 1])
plt.figure(figsize=(8,5),dpi = 50)
plt.scatter(x1,y1,color = 'blue',marker='x',label = 'negetive sample')
plt.scatter(x2,y2,color = 'red',marker='o',label = 'postive sample')
plt.legend(loc='lower left')
plt.xlabel('score1')
plt.ylabel('score2')
plt.show()
第二种，
positive = data[data.admitted.isin(['1'])] # 1
negetive = data[data.admitted.isin(['0'])] # 0
plt.figure(figsize=(8,5),dpi = 50)
plt.scatter(positive['score1'],positive['score2'],color = 'blue',marker='x',label = 'negetive sample')
plt.scatter(negetive['score1'],negetive['score2'],color = 'red',marker='o',label = 'postive sample')
plt.legend(loc='lower left')
plt.xlabel('score1')
plt.ylabel('score2')
plt.show()
可以看出两类间，有一个清晰的决策边界。
1.2 Sigmoid function
def sigmoid(z):
return 1/(1+np.exp(-z))
xx = np.arange(-10,10,0.1)
plt.figure(figsize=(8,5),dpi = 50)
plt.plot(xx,sigmoid(xx))
plt.show()
1.3 Cost function(损失函数)
# 定义逻辑回归代价函数（cost function）
def costfunction(theta,x,y):
first = (-y) * np.log(sigmoid(x @ theta))
second = (1-y) * np.log(1- sigmoid(x @ theta))
costf =np.mean(first - second)
return costf
# 获取数据集数据
# add a ones column - this makes the matrix multiplication work out easier
if 'Ones' not in data.columns:
data.insert(0, 'Ones', 1)
#ones = pd.DataFrame({'ones':np.ones(len(data))})
#data = pd.concat([ones,data],axis=1)
# # 合并数据方法二concat，根据列合并axis=1
# set X (training data) and y (target variable)
# .values是将Dataframe的表格型数据转换成数组，as_matrix已经被淘汰
x = data.iloc[:, :-1].values # Convert the frame to its Numpy-array representation.
y = data.iloc[:, -1].values # Return is NOT a Numpy-matrix, rather, a Numpy-array.
theta = np.zeros(x.shape[1])
# 检查数据集的维度
print(x.shape,y.shape,theta.shape)
# 计算代价函数
print(costfunction(theta,x,y))
接下来，我们需要一个函数来计算我们的训练数据、标签和一些参数thate的梯度。
1.4 Gradient（梯度下降）
# 定义梯度下降函数
def Gradient(theta,x,y):
gradient =(x.T @ (sigmoid(x @ theta) - y))/len(x)
return gradient
print(Gradient(theta,x,y))
1.5 Learning θ parameters（theta 参数）
注意，我们实际上没有在这个函数中执行梯度下降，我们仅仅在计算梯度。
# 高级优化算法计算成本和梯度参数
import scipy.optimize as opt
result = opt.fmin_tnc(func = costfunction, x0 =theta,fprime=Gradient,args = (x,y) )
print(result)
下面是第二种方法，结果是一样的
res = opt.minimize(fun = costfunction,x0=theta, args=(x, y), method='TNC',jac = Gradient )
print(res)
# 返回结果中res.x就是theta
fun: 0.2034977015894744
jac: array([9.11457705e-09, 9.59621025e-08, 4.84073722e-07])
message: 'Local minimum reached (|pg| ~= 0)'
nfev: 36
nit: 17
status: 0
success: True
x: array([-25.16131867, 0.20623159, 0.20147149])
print(costfunction(result[0],x,y))
1.6 Evaluating logistic regression（评估logistic回归）
def predict(theta,x):
probability = sigmoid(x @ theta)
return [1 if a >= 0.5 else 0 for a in probability] # return a list
# 第二种写法
#return (probability >= 0.5).astype(int)# 变量类型转换
final_theta = result[0]
prediction = predict(final_theta,x)
print(prediction)
# 方法一
acc_len = 0
for i in range(len(prediction)):
if prediction[i] == y[i]:
acc_len = acc_len+1
accuracy = acc_len/len(prediction)
print(accuracy)
# 方法二：zip()函数
correct = [1 if a==b else 0 for (a, b) in zip(prediction, y)]
accuracy = sum(correct) / len(x)
print(accuracy)
精度达到89%。
也可以用skearn中的方法来检验。
from sklearn.metrics import classification_report
print(classification_report(prediction, y))
precision recall f1-score support
0 0.85 0.87 0.86 39
1 0.92 0.90 0.91 61
avg / total 0.89 0.89 0.89 100
1.7 Decision boundary（决策边界）
x1 = np.arange(130,step = 0.1)
x2 = -(final_theta[0]+x1* final_theta[1]) / final_theta[2]
plt.figure(figsize=(8,5),dpi = 50)
plt.scatter(positive['score1'],positive['score2'],color = 'blue',marker='x',label = 'negetive sample')
plt.scatter(negetive['score1'],negetive['score2'],color = 'red',marker='o',label = 'postive sample')
plt.plot(x1,x2)
plt.xlabel('x1')
plt.ylabel('x2')
plt.legend()
plt.title('Decision Boundary')
plt.show()
2 Regularized logistic regression(正则化逻辑回归)
加入正则项提升逻辑回归算法。正则化是成本函数中的一个术语，它使算法更倾向于“更简单”的模型（在这种情况下，模型将更小的系数）。有助于减少过拟合，提高模型的泛化能力。
2.1 Visualizing the data （数据可视化）
plt.style.use('fivethirtyeight') # 样式美化
path = 'D:\文档\ex2data2.txt'
data2 = pd.read_csv(path,header=None,names = ['Test1','Test2','Accepted'])
print(data2.head())
postive = data2[data2.Accepted.isin(['1'])]
negetive = data2[data2.Accepted.isin(['0'])]
print(postive)
plt.figure(figsize=(8,5),dpi = 50)
plt.scatter(postive['Test1'],postive['Test2'],label = 'postive',color = 'blue')
plt.scatter(negetive['Test1'],negetive['Test2'],label = 'negetive',color = 'red',marker= 'x')
plt.xlabel('Test1')
plt.ylabel('Test2')
plt.legend()
plt.show()
注意到其中的正负两类数据并没有线性的决策界限。因此直接用logistic回归在这个数据集上并不能表现良好，因为它只能用来寻找一个线性的决策边界。
2.2 Feature mapping(特征映射)
一个拟合数据的更好的方法是从每个数据点创建更多的特征。
我们将把这些特征映射到所有的x1和x2的多项式项上，直到第六次幂。
for i in 0..power
for p in 0..i:
output x1^(i-p) * x2^p```
# 定义特征缩放
def feature_mapping(power,x,y):
data = {}
for i in np.arange(power+1):
for p in np.arange(i+1):
data['f{}{}'.format(i-p,p)] = np.power(x,i-p) * np.power(y,p)
data = pd.DataFrame(data)
return data
#.values是dataframe类对象的一个属性，不是方法
x1 = data2['Test1'].values
y1 = data2['Test2'].values
data = feature_mapping(6,x1,y1)
#print(data)
print(data.shape)
print(data.head())
经过映射，我们将有两个特征的向量转化成了一个28维的向量。
2.3 Regularized Cost function（正则化损失函数）
加入正则化参数，防止出现过拟合。
# 定义sigmoid/logistic函数
def sigmoid(z):
return 1/(1+np.exp(-z))
# 定义正则化损失函数
def regular_costf(x,y,theta,lam):
first = - y * np.log(sigmoid(x @ theta))
second = -(1-y) * np.log(1-sigmoid(x @ theta))
third = theta[1:]
return np.mean(first+second)+ (lam/(2*len(x)))* np.power(third,2).sum()
# 数据x,y,theta获取
x = data.values
y = data2['Accepted'].values
theta = np.zeros(x.shape[1])
print(regular_costf(x,y,theta,lam=1))
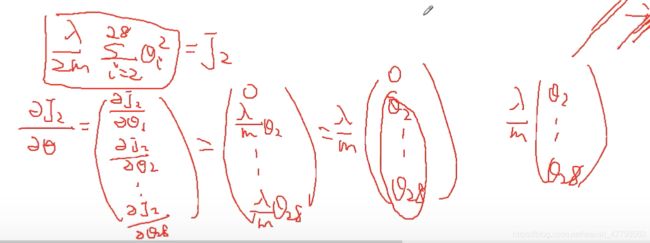
2.4 Regularized gradient（正则化梯度下降）
# 梯度下降算法
def Gradient(theta,x,y):
gradient =(x.T @ (sigmoid(x @ theta) - y))/len(x)
return gradient
# 正则化梯度下降算法
def regular_gradient(theta,lam,x,y):
reg = (lam/len(x))*theta
reg[0] = 0
return Gradient(theta,x,y)+reg
print(regular_gradient(theta,1,x,y))
2.5 Learning parameters
# 优化算法minimize()
import scipy.optimize as opt
# result = opt.minimize(fun=regular_costf,x0=theta,args=(x,y,1),method='CG',jac=regular_gradient)
# print(result)
result2 = opt.fmin_tnc(func=regular_costf, x0=theta, fprime=regular_gradient, args=(x, y, 2))
print(result2)
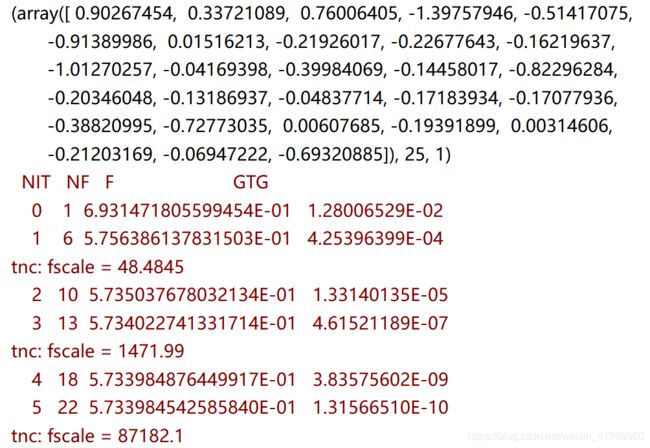
我们还可以使用Python库scikit-learn来解决这个问题。
from sklearn import linear_model#调用sklearn的线性回归包
model = linear_model.LogisticRegression(penalty='l2', C=1.0)
model.fit(x, y.ravel())
print(model.score(x, y))
2.6 Evaluating logistic regression（评估logistic回归）
final_theta = result2[0]
# 定义预测函数
def predict(theta,x):
probability = sigmoid(x @ theta)
return [1 if i>=0.5 else 0 for i in probability]
predictions = predict(final_theta,x)
correct = [1 if a==b else 0 for (a,b) in zip(predictions,y)]
accuracy = sum(correct) / len(correct)
print(accuracy)
或者用skearn中的方法来评估结果。
from sklearn.metrics import classification_report
print(classification_report(y, predictions))
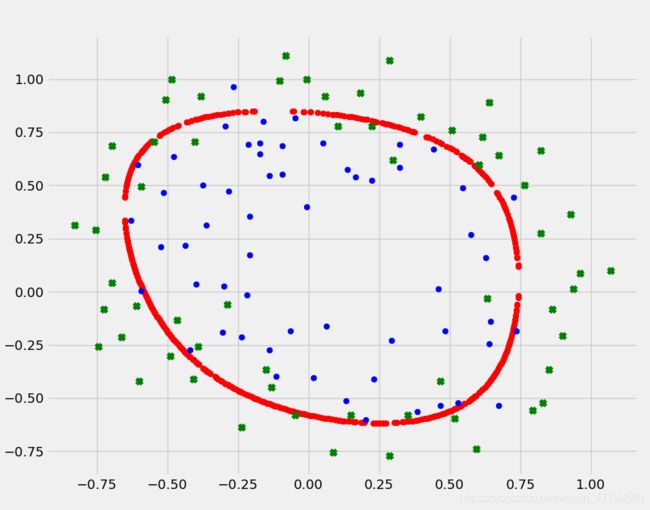
2.7 Decision boundary（决策边界）
# 画出决定边界
density = 1000
threshhold = 2 * 10 ** -3
def find_decision_boundary(density, power, theta, threshhold):
t1 = np.linspace(-1, 1.5, density)
t2 = np.linspace(-1, 1.5, density)
cordinates = [(x, y) for x in t1 for y in t2]
x_cord, y_cord = zip(*cordinates)
mapped_cord = feature_mapping(power,x_cord, y_cord) # this is a dataframe
inner_product = mapped_cord.values @ theta
decision = mapped_cord[np.abs(inner_product) < threshhold]
# f10和f01分别为x,y
return decision.f10, decision.f01
# 寻找决策边界函数
x, y = find_decision_boundary(density, 6, final_theta, threshhold)
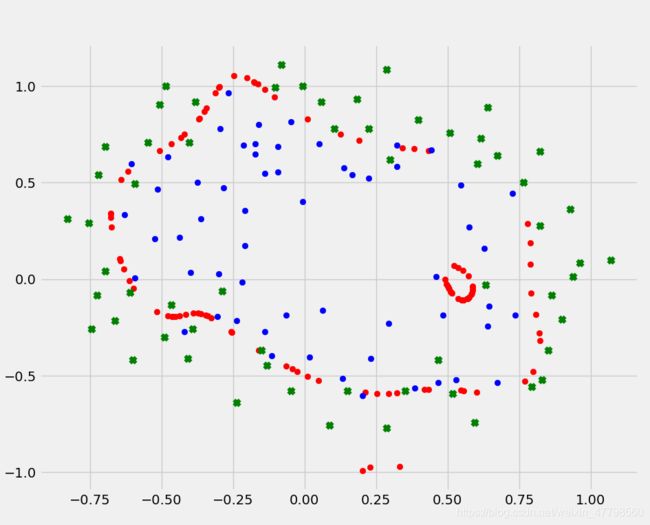
plt.figure(figsize=(10,8),dpi = 50)
plt.scatter(x,y,color = 'red')
postive = data2[data2.Accepted.isin(['1'])]
negetive = data2[data2.Accepted.isin(['0'])]
plt.scatter(postive['Test1'],postive['Test2'],label = 'postive',color = 'blue')
plt.scatter(negetive['Test1'],negetive['Test2'],label = 'negetive',color = 'green',marker= 'x')
plt.legend()
plt.show()
用等高线的方法绘制决策边界：
改变正则化参数λ，并查看决策边界的变化效果。
上图为 λ=1 的情况，拟合效果不错。
图2为λ=0时，出现的过拟合现象。
图3为λ=100时，出现的欠拟合现象。