梯度下降法原理及python实现

引言

梯度下降法不是机器学习算法，不能用来解决分类或回归问题，而是一种基于搜索的最优化方法，作用是优化目标函数，如求损失函数的最小值，即梯度下降法。

梯度

梯度的本意是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）。

如单变量函数y=x²，其导数为$\nabla$y=2*x，此时在x=2处的梯度为4，如果函数为多变量函数，梯度则为一个向量($\frac{\partial y}{x_1}$,……,$\frac{\partial y}{x_i}$)，梯度的方向指出了函数在给定点上升最快的方向，取负则为下降最快方向。

单变量梯度下降法

单变量梯度下降原理

假设函数为$J(\theta )=(\theta -2{)}^2+1$，对函数求导得到$J\prime (\theta )=2\ast \theta -4$，假设初始值为1，即${\theta }^0=1$，学习率为0.01，即$\alpha =0.01$
根据梯度下降公式$${\theta }^1={\theta }^0-\alpha \ast J\prime ({\theta }^0)$$$${\theta }^2={\theta }^1-\alpha \ast J\prime ({\theta }^1)$$$$\dots \dots$$$${\theta }^i={\theta }^{i-1}-\alpha \ast J\prime ({\theta }^{i-1})$$当${\theta }^i$小于我们设置的预期值时，此时认为到达函数最低点。

python实现单变量梯度下降

def J(theta):
    return (theta-2)**2+1
def dJ(theta):
    return 2*theta-4

theta = 1.0
alpha = 0.01

extreme = 1e-8
while True:
    last_theta = theta
    theta = last_theta - alpha * dJ(last_theta)
    if abs(J(theta)-J(last_theta)) < extreme :
        break
        
print(theta)
print(J(theta))


输出
1.9995076992061676
1.0000002423600716

批量梯度下降法

批量梯度下降法原理

在线性回归分析法中，我们的目标是求得损失函数最小值$$\sum _{i=1}^m(y^{(i)}-{\hat{y}}^{(i)}{)}^2$$$${\hat{y}}^{(i)}={\theta }_0+{\theta }_1{X}_1^{(i)}+{\theta }_2{X}_2^{(i)}+\dots \dots +{\theta }_n{X}_n^{(i)}$$对所有$\theta$求导得

$X_b$为矩阵$X$左边加一列1，为了使得求出的梯度和样本$m$无关，对损失函数除以$m$，得到

最终得到的结果是一个矩阵运算

python实现多变量梯度下降

import numpy as np

#损失函数
def J(theta,x_b,y_train):
    return np.sum(y_test-x_b.dot(theta))**2 / len(y_train)

#对损失函数求导
def dJ(theta,x_b,y_train):
    return x_b.T.dot(x_b.dot(theta) - y_train) * 2. / len(x_b)

#梯度下降
def gradient_descent(x_b,y_train,initial_theta,alpha,n_iters = 1e4,epsilon = 1e-8):
    theta = initial_theta
    #梯度下降次数
    i_iter = 0
    
    while i_iter<n_iters:
        gradient = dJ(theta,x_b,y_train)
        last_theta = theta
        theta = theta-alpha*gradient
        
        if abs(J(theta,x_b,y_train) - J(theta,x_b,y_train)) < epsilon :
            break
            
        i_iter += 1
        
    return theta

#测试数据集测试
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
boston = load_boston()
x_data = boston.data
y_data = boston.target
x_train,x_test,y_train,y_test = train_test_split(x_data,y_data)

x_b = np.hstack([np.ones((len(y_train),1)),x_train])
x_test = np.hstack([np.ones((len(x_test),1)),x_test])
initial_theta = np.zeros(x_b.shape[1])
res = gradient_descent(x_b,y_train,initial_theta,0.001)

梯度下降算法数据归一化

用正规方程求解线性回归算法时，由于求解损失函数看作是正规方程计算，因此不需要对数据归一化处理，而使用梯度下降法时，由于存在变量alpha，当数据不在一个维度时，将会影响梯度的结果，而梯度乘以alpah是每步的步长，这将导致步长太大或太小，太大导致结果不收敛，太小导致搜索结果太慢，因此需要对数据进行归一化处理。

from sklearn.preprocessing import StandardScaler
standard_scaler = StandardScaler()
standard_scaler.fit(x_train)
x_train_standard = standard_scaler.transform(x_train)
x_test_standard = standard_scaler.transform(x_test)

随机梯度下降法

随机梯度下降原理

上面说的梯度下降法需要对$m$个样本都进行计算，这称之为批量梯度下降法，当样本量非常大时，计算量也非常大，此时可以选取$m$个样本中的一个进行搜索，这种方法称之为随机梯度。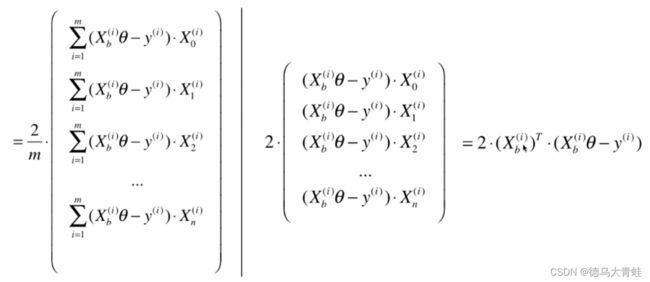
随机梯度下降搜索的方向可能不是梯度下降最快的方向，但是最终的结果还是会在最小值的附近，当样本量非常大时，损失一定的精度来换取计算时间是值得的，在随机梯度下降法中学习率alpha的取值非常重要，如果alpha取固定值，到结果非常接近最小值时，由于alpha取固定值，计算结果可能跳出最小值范围，因此在随机梯度中，alpha一般随着随机次数慢慢减小。$$\alpha =\frac{a}{iters+b}$$

python实现随机梯度下降算法

import numpy as np
import matplotlib.pyplot as plt
m = 1000
x = np.random.normal(size=m)
y = 4.*x+3.+np.random.normal(0,1,size=m)
x = x.reshape(-1,1)

def dJ_sgd(theta,x_b_i,y_i):
    return x_b_i * (x_b_i.dot(theta) - y_i) * 2.

def sgd(initial_theta,x_b,y,n_iters):
    t0 = 5
    t1 = 50
    def learning_rate(t):
        return t0/(t1+t)
    
    theta = initial_theta
    for cur_iter in range(n_iters):
        #对m行进行乱序
        index = np.random.permutation(m)
        #打乱顺序后的x,y
        x_b_new = x_b[index]
        y_new = y[index]
        for i in range(m):
            gradient = dJ_sgd(theta,x_b_new[i],y_new[i])
            theta = theta - learning_rate(cur_iter*m)*gradient
  
    return theta
   
x_b = np.hstack([np.ones((len(x),1)),x])
print(x_b.shape)
initial_theta = np.zeros(x_b.shape[1])
#样本循环5次，每行都循环到
theta = sgd(initial_theta,x_b,y,n_iters=5)
print(theta)
   
#最终求得的theta为[2.69782774 4.        ]

小批量梯度下降法

小批量梯度下降法原理

每次不看全部样本，也不只看一个样本，选取$m$个样本中的$n$个，$m>n>1$，这样梯度下降的过程即能兼顾计算速度，得到的结果精度也比随机梯度下降要高。

python实现小批量梯度下降法

import numpy as np

m = 1000
x = np.random.normal(size=m)
y = 4. * x + 3. + np.random.normal(1,3,size=m)
print(y.shape)
x = x.reshape(-1, 1)

def dJ_sgd(theta, x_b_i, y_i):
    return x_b_i.T.dot(x_b_i.dot(theta) - y_i) * 2. / len(x_b_i)


def sgd(initial_theta, x_b, y, n_iters, k):
    t0 = 5
    t1 = 50

    def learning_rate(t):
        return t0 / (t1 + t)

    theta = initial_theta
    for cur_iter in range(n_iters):
        # 对m行进行乱序
        index = np.random.permutation(m)
        # 打乱顺序后的x,y
        x_b_new = x_b[index]
        y_new = y[index]
        for i in range(m):
            #每次取样本m中的k个
            gradient = dJ_sgd(theta, x_b_new[i:i+k], y_new[i:i+k])
            theta = theta - learning_rate(cur_iter * m) * gradient

    return theta

X_b = np.hstack([np.ones((len(x), 1)), x])
initial_theta = np.zeros(X_b.shape[1])
# 所有样本循环5次，每次取5行
theta = sgd(initial_theta,X_b, y,n_iters=5, k=5)
print(theta)

#结果[3.88001633 4.06103233]

sklearn实现随机梯度下降

from sklearn.linear_model import SGDRegressor
from sklearn.datasets import load_boston     
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

boston = load_boston()
x_data = boston.data
y_data = boston.target
x_train,x_test,y_train,y_test = train_test_split(x_data,y_data)
#数据归一化处理
standard_scaler = StandardScaler()
standard_scaler.fit(x_train)
x_train_standard = standard_scaler.transform(x_train)
x_test_standard = standard_scaler.transform(x_test)

#循环次数
sgd_reg = SGDRegressor(n_iter_no_change=9000)
sgd_reg.fit(x_train_standard,y_train)
sgd_reg.score(x_test_standard,y_test)