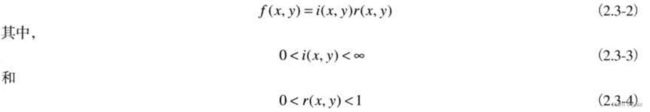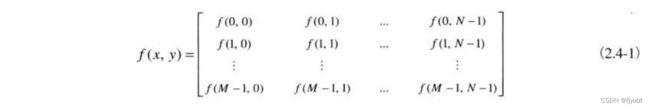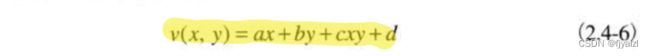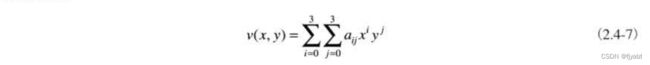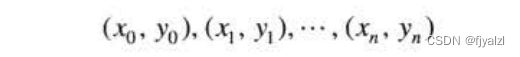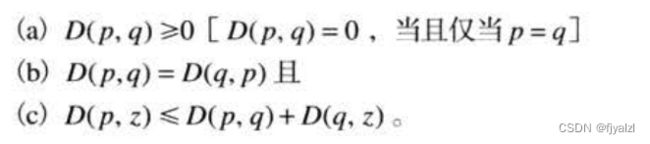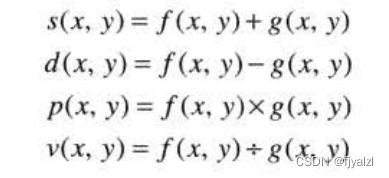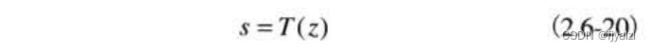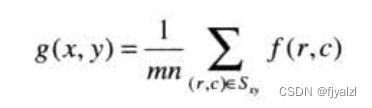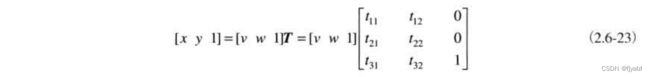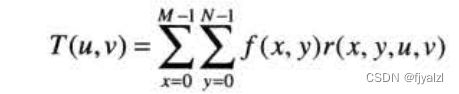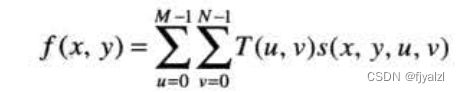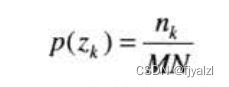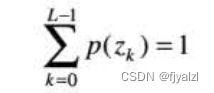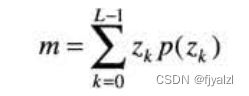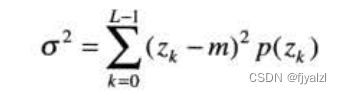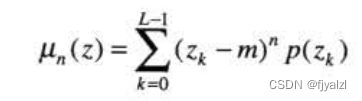数字图像处理 第二章 数字图像基础
2.1 视觉感知要素
2.1.1 人眼的结构
锥状细胞对颜色高度敏感，能够充分分辨图像细节。锥状体视觉称为白昼视觉或量视觉。
杆状细胞没有彩色感觉，而对低照明度敏感。杆状体视觉称为暗视觉或微光视觉。
2.1.2 眼睛中图像的形成
晶状体和成像区域（视网膜）之间的距离是固定的，实现正常聚焦的焦距是通过改变晶状体的形状来得到的。
视网膜图像主要聚焦在中央凹区域。然后，光接收器的相对刺激作用产生感知，把辐射能转变为电脉冲，最后由大脑解码。
2.1.3 亮度适应和辨别
因为数字图像作为离散的灰度集来显示，所以眼睛对不同亮度级别之间的辨别能力在显示图像处理结果中是一个重要的考虑因素。
眼睛可以同时辨别的不同强度级别的总范围与整个适应范围相比是很小的。对于任何给定的条件集合，视觉系统的当前灵敏度级别称为亮度适应级别，在任何特定的适应级别上，人眼辨别光强变化的能力也是值得考虑的因素。
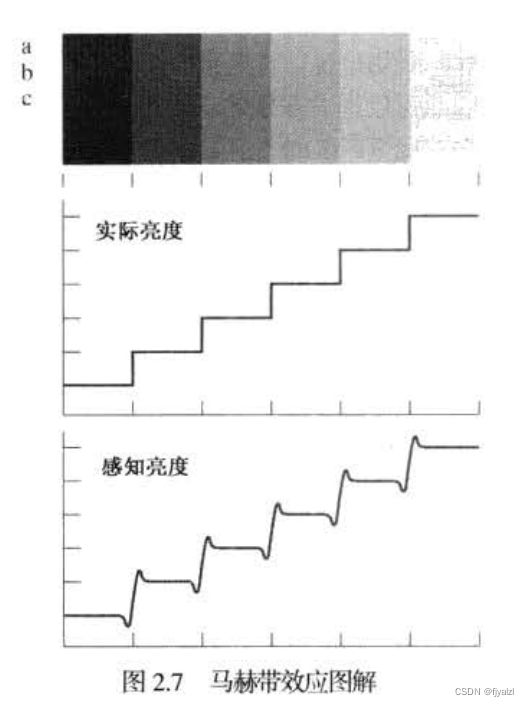
两种现象清楚地表明感知亮度不是简单地强度的函数。
第一种现象基于这样一个事实，即视觉系统往往会在不同强度区域的边界处出现“下冲”或“上冲”现象。图2.7（a）显示了这种现象的一个典型例子。虽然条带的强度恒定，但在靠近边界处我们实际上感知到了带有毛边的亮度模式【见图2.7（c）】。这些看起来带有毛边的带称为马赫带。
第二种现象称为同时对比，它与这样一个事实有关，即感知区域的亮度并不简单地取决于其强度。
人类感知现象的另一些例子就是错觉，在错觉中，眼睛填充了不存在的信息或者错误地感知了物体的几何特点。
2.2 光和电磁波谱
波长和频率的关系可用下式描述：
其中c是光速（2.998X
m/s）。电磁波谱的各个分量的能量由下式给出：
其中h是普朗克常数。波长的单位是米，最常用的单位是微米和纳米。频率用赫兹来度量，1Hz表示正弦波每秒1个周期。常用能量单位是电子伏特。
没有颜色的光称为单色光或无色光。单色光的唯一属性是它的强度或大小。灰度级一词通常用来表示单色光的强度。从黑到白的单色光的度量值范围通常称为灰度级，而单色图像常称为灰度图像。
有三个基本量用于描述彩色光源的质量：发光强度、光通量和亮度。发光强度是从光源流出能量的总量，通常用瓦特（w）来度量；用流明数（lm）度量的光通量给出观察者从光源感受到的能量；亮度是光感知的主观描绘子，它实际上不能度量。
2.3 图像感知和获取
我们感兴趣的多数图形都是由“照射”源和形成图像的“场景”元素对光能的反射或吸收而产生的。
照射也可以由非传统光源甚至由计算机产生的照射模式产生。类似地，场景元素可能是熟悉的物体，但他们也可能是分子、沉积岩或人类的大脑。依赖光源的特性，照射被物体反射或透射。
2.3.1 使用单个传感器获取图像
2.3.2 使用条带传感器获取图像
2.3.3 使用传感器阵列获取图像
2.3.4 简单地图像形成模型
当一副图像由物体过程产生时，其亮度值正比于物理源所辐射的能量。因此，f(x,y)一定是非零的和有限的，即
函数f(x,y)可由两个分量来表征：（1）入射到被观察场景的光源照射总量；（2）场景中物体所反射的光照总量。这两个分类分别称为入射分量和反射分量，且分别表示为i(x,y)和r(x,y)。两个函数作为一个乘积合并形成f(x,y)，即
令单色图像在任何坐标（x0,y0）处的强度（灰度）表示为
理论上，仅要求Lmin为正，而要求Lmax为有限值。
2.4 图像取样和量化
2.4.1 取样和量化的基本概念
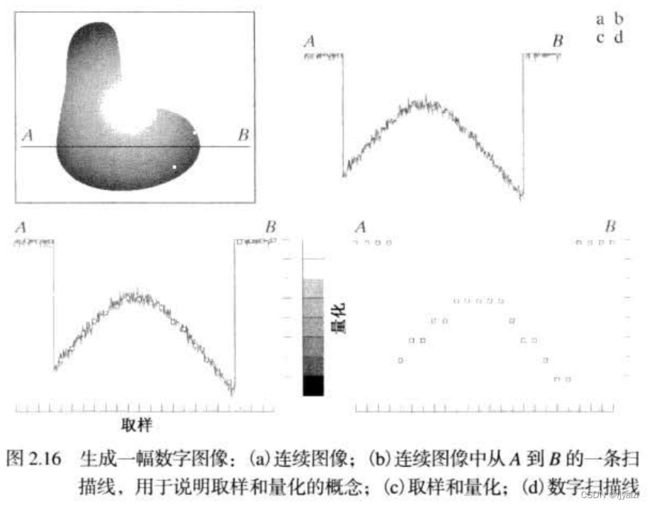
图2.16说明了取样和量化的基本概念。图2.16（a）显示了一幅连续图像f，我们想把它转换为数字形式。一幅图像的x和y坐标及幅度可能都是连续的。为将它转换为数字形式，必须在坐标上和幅度上都进行取样操作。对坐标值进行数字化称为取样，对幅值数字化称为量化。
2.4.2 数字图像表示
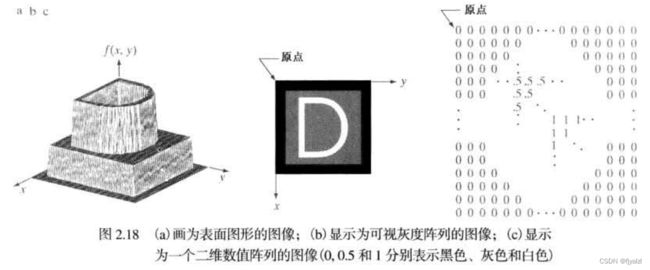
有三种基本方法表示f(x,y)。（a）是一幅函数图，用两个坐标轴决定空间位置，第三个坐标是以两个空间变量x和y为函数的f（灰度）值。
（b）是更一般的表示。它显示了f(x,y)出现在监视器或照片上的情况。这里，每个点的灰度与该点处的f值成正比。该图中仅有三个等间隔的灰度值。如果灰度被归一化到区间【0,1】内，那么图像中每个点的灰度都有0,0.5或1这样的值。监视器或打印机简单地把这三个值分别变换成黑色、灰色、或白色。
第三种表示是将f(x,y)的数值简单地显示为一个阵列（矩阵）。
图像显示允许我们快速地观察结果。数值阵列用于处理和算法开发。以公式形式，我们可将一个MXN的数值阵列表示为
该式的两边以等效的方式定量地表达了一幅数字图像。右边是一个实数矩阵，该矩阵中的每个元素称为图像单元、图像元素或像素。
数字图像的原点位于左上角，其中正x轴向下延伸，正y轴向右延伸。这种方便的表示基于这样的吗事实：许多图像显示扫描都是从左上角开始的，然后一次向下移动一行。更重要的事实是矩阵的第一个元素按惯例应在阵列的左上角，因此，将f(x,y)的原点选择在左上角于数学上是讲得通的。
2.4.3 空间和灰度分辨率
直观上看，空间分辨率是图像中可辨别的最小细节的度量。在数量上，空间分辨率可以有很多方法来说明，其中每单位距离线对数和每单位距离点数（像素数）是最通用的度量。
类似地，灰度分辨率是指在灰度级中可分辨的最小变化。
2.4.4 图像内插
内插是在诸如放大、收缩、旋转和几何校正等任务中广泛应用的基本工具。
从根本上看，内插是用已知数据来估计未知位置的数值的处理。方法包括：
双线性内插：
双三次内插：
2.5 像素间的一些基本关系
2.5.1 相邻像素
p的4邻域：
p的4个对角相邻像素坐标：
这些点与4个邻点一起称为p的8邻域。用N8（p）表示。
2.5.2 邻接性、连通性、区域和边界
混合邻接是8邻接的改进。混合邻接的引入是为了消除采用8邻接时产生的二义性。
从具有坐标（x,y）的像素p到具有坐标（s,t）的像素q的通路（或曲线）是特定的像素序列，其坐标为
n是通路的长度。如果（x0,y0）=（xn,yn），则通路是闭合通路。可以依据特定的邻接类型定义4邻接、8邻接或m邻接。
令S是图像中的一个像素子集。如果S的全部像素之间存在一个通路，则可以说两个像素p和q在S中是连通的。对于S中的任何像素p，S中连通到该像素的像素集称为S的连通分量。如果S仅有一个连通分量，则集合S称为连通集。
令R是图像中的一个像素子集。如果R是连通集，则称R为一个区域。两个区域，如果它们联合形成一个连通集，则区域Ri和Rj称为邻接区域。不邻接的区域称为不连接区域。
2.5.3 距离度量
对于坐标分别为（x,y），（s,t）和（v,w）的像素p，q和z，如果
则D是距离函数或度量。p和q间的欧几里得距离定义如下：
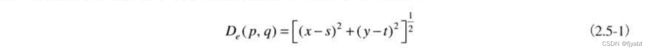对于距离度量，距点（x,y）的距离小于或等于某个值r的像素是中心在（x,y）且半径为r的圆平面。p和q间的距离D4（又称为城市街区距离）由下式定义：
在这种情况下，距（x,y）的距离D4小于或等于某个值r的像素形成一个中心在（x,y）的菱形。例如：距中心点（x,y）的距离D4小于或等于2的像素，形成固定距离的下列轮廓：
其中D4=1的像素是（x,y）的4邻域。
p和q间的D8距离（又称为棋盘距离）由下式定义：
在这种情况下，距（x,y）的D8距离小于或等于某个值r的像素形成中心在（x,y）的方形。例如，距中心点（x,y）的D8距离小于或等于2的像素形成下列固定距离的轮廓：
其中D8=1的像素是（x,y）的8邻域。
p和q之间D4距离和D8距离与任何通路无冠，通路可能存在于各点之间，因为这些距离仅与该点的坐标有关。然而，如果选择考虑m邻接，则两点间的Dm距离用点间的最短通路定义。在这种情况下，两个像素间的距离将依赖于沿通路的像素值及其邻点值。
2.6 数字图像处理中所用数学工具的介绍
2.6.1 阵列与矩阵操作
2.6.2 线性操作与非线性操作
一般算子：
如果
则称H是一个线性算子，其中ai,aj,fi(x,y)和fj(x,y)分别是任意常常数和图像（大小相同）。
2.6.3 算术操作
图像间的算术操作是阵列操作。4种算术操作表示为
2.6.4 集合和逻辑操作
基本集合操作
令A为一个实数序对组成的集合。如果a是A的一个元素，则
同样，如果a不是A的一个元素，则写成
不包含任何元素的集合称为空集。
集合、子集、并集、交集的表示
逻辑操作
处理二值图像时，吧图像想象为前景（1值）与背景（0值）。然后将区域（目标）定义为由前景像素组成，则集合操作就变成了二值图像中目标坐标间的操作。
模糊集合
2.6.5 空间操作
空间操作直接在给定图像的像素上执行。分为三大类：（1）单像素操作；（2）邻域操作；（3）几何空间变换。
单像素操作
灰度为基础改变单个像素的值：
其中，z是原图像中像素的灰度，s是处理后的图像中相应像素的（映射）灰度。
邻域操作
令Sxy代表图像f中以任意一点（x,y）为中心的一个邻域的坐标集。邻域处理在输出图像g中的相同坐标处生成一个相应的像素，该像素的值由输入图像中坐标在Sxy内的像素经指定操作决定。
其中r和c是像素的行和列坐标，这些坐标是Sxy中的成员。
几何空间变换和图像配准
几何变换由两个基本操作组成：（1）坐标的空间变换；（2）灰度内插，即对空间变换后的像素赋灰度值。
坐标变换表示：
其中，（v,w）是原图像中像素的坐标，（x,y）是变换后图像中像素的坐标。
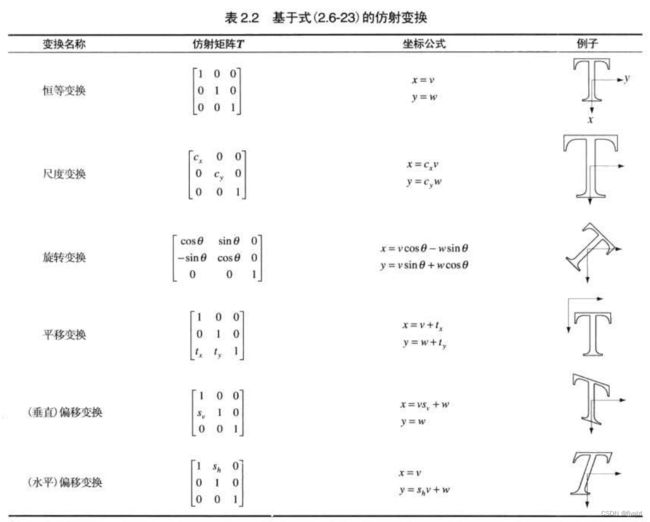
最常用的空间坐标变换之一是仿射变换，其一般形式如下：
这个变换可根据矩阵T中元素所选择的值，对一组坐标点做尺度、旋转、平移或偏移。
两种映射基本方法：前向映射、反向映射。
2.6.6 向量与矩阵操作
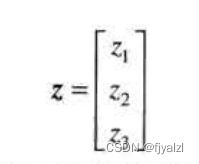
RGB图像每个像素都有三个分量，这些分量可组织称一个列向量形式：
三个元素表示红、绿、蓝三种颜色图像中像素亮度。
一个像素向量z和一个任意点a在n维空间的欧氏距离D可以用一个向量积定义：
线性变换：
更广范围的图像线性处理：
2.6.7 图像变换
二维线性变换通用形式
反变换
线性变换域中操作的一般方法
2.6.8 概率方法
灰度级zk出现概率估计
nk为灰度zk在图像中出现的次数，MN是像素总数
平均灰度
灰度的方差
随机变量z关于均值的第n阶矩阵定义为
小结
本章主要为后续的讨论提供了知识背景。首先对人类视觉系统和光、电磁波谱的论述介绍了图像感知和图像来源的基本概念，之后论述的图像模型、取样和内插等概念为之后章节学习做铺垫。书籍中在本章介绍了大量理论知识，其中包含了许多公式，难以在短时间内吸收消化。希望在后续学习中，通过结合实例应用能够有更深的体会。