论文笔记（二十二）：GRiD: GPU-Accelerated Rigid Body Dynamics with Analytical Gradients

文章概括

作者：Brian Plancher, Sabrina M. Neuman, Radhika Ghosal, Scott Kuindersma, Vijay Janapa Reddi
来源：2022 IEEE International Conference on Robotics and Automation (ICRA) May 23-27, 2022. Philadelphia, PA, USA
原文：https://ieeexplore.ieee.org/abstract/document/9812384
代码、数据和视频：
系列文章目录：
上一篇：
论文笔记（二十一）：Fusing Joint Measurements and Visual Features for In-Hand Object Pose Estimation
下一篇：

摘要

我们介绍了 GRiD：一个 GPU 加速库，用于计算具有解析梯度的刚体动力学。 GRiD 旨在加速最先进的机器人规划、控制和机器学习中使用的非线性轨迹优化子问题，这需要在每次迭代中对刚体动力学及其梯度进行数十到数百次自然并行计算。 GRiD 利用 URDF 解析和代码生成来提供优化的动态内核，这些内核不仅公开了 GPU 友好的计算模式，而且还利用了每个计算中的细粒度并行性和计算之间的粗粒度并行性。通过这种方法，当执行刚体动力学算法的多个计算时，GRiD 提供了比最先进的多线程 CPU 实现高达 7.2 倍的加速，并且在计算时保持高达 2.5 倍的加速用于 I/O 开销。我们将 GRiD 作为开源库发布，供更广泛的机器人社区使用。

1. 介绍

刚体动力学及其梯度的有效实现已成为机器人应用的关键计算内核。 最初主要用于高自由度机器人 [1]、[2]、[3]、[4] 的基于模型的规划和控制系统的非线性轨迹优化子问题，这些计算内核也在不断增长 机器学习 (ML) 技术的重要性 [5]、[6]、[7]、[8]、[9]。

尽管高度精确和优化，但现有的基于空间代数的刚体动力学方法的实现[10]并没有利用算法中存在的并行机会，限制了其性能[11], [12], [13], [14]。这一点很关键，因为在机器人学中涉及刚体动力学的许多瓶颈计算中存在自然的并行性[15], [16], [9]。例如，前向动力学的梯度占典型的非线性模型预测控制（MPC）实现的30%到90%[17], [18], [12], [16]，并且在轨迹的离散点上是自然并行的。

虽然对并行计算的需求越来越大，但多核CPU的性能一直受到热耗散的限制，强制执行的利用墙限制了单个芯片可以提供的性能[19], [20]。这促使人们越来越多地使用GPU，它可以通过在单个芯片内支持更大规模的并行性而提供更高的性能机会。

在这项工作中，我们介绍了GRiD，一个基于空间代数的刚体动力学及其分析梯度的GPU加速库。GRiD被设计用来加速最先进的机器人规划、控制和机器学习算法中使用的非线性轨迹优化子问题。GRiD经过优化，使用GPU线程块来计算这些算法中发现的几十到几百个刚体动力学及其梯度的自然并行计算，并实现了最先进的轨迹优化中使用的更精确的基于空间代数的刚体动力学公式[21], [22], [23], [24]。GRiD建立在最近的工作基础上，该工作设计了一个手动优化的GPU实现刚体动力学梯度的七连杆串行链操纵器[25]，提供进一步的优化和概括，以支持多种动力学算法，URDF解析大多数常见的机器人模型，并优化代码生成。

GRiD不仅释放了非线性轨迹优化完全在GPU上运行的能力，而且在进行刚体动力学及其梯度的多重计算时，它还比在高性能工作站上运行的最先进的多线程CPU实现的速度快7.2倍。GRiD还可以使用GPU作为在主机CPU上计算的刚体物理学加速器，在考虑到CPU和GPU之间的I/O通信开销时，保持高达2.5倍的速度提升。

我们将GRiD作为一个开源库发布，使机器人研究人员能够更好地探索和利用GPU平台上大规模并行的性能收益。我们的库可以在https://github.com/robot-acceleration/grid。

2. 相关工作

GRiD旨在提供通用的、基于空间代数的、具有分析梯度的动力学，并通过GPU上的大规模并行性来加速它们。

虽然现有许多最先进的基于空间代数的刚体动力学库[26]、[11]、[13]、[27]、[28]，但这些库都没有针对GPU进行优化[16]。最近发布的NVIDIA Isaac Sim[29]是个例外，它在GPU上支持基于空间代数的正向模拟，但不支持梯度。

因此，先前使用基于空间代数的方法对 GPU 进行规划和控制的工作要么仅限于汽车、无人机和其他低自由度系统 [15]，要么依赖于手动优化的刚体动力学实现 及其特定机器人模型的梯度 [16]、[25]。 大多数利用基于空间代数的刚体动力学的机器学习方法都依赖于上述库 [9]、[29]。

历史上，GPU也被用来通过数值微分加速梯度计算[38], [39]。然而，这些方法在用于机器人规划、控制和机器学习时，已被证明具有不太有利的数值特性。

3. 背景

A. 计算硬件：CPU vs. GPU

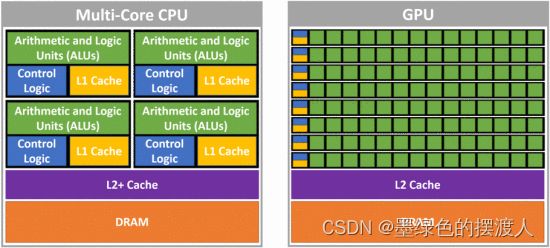
与多核CPU相比，GPU有一套大得多的简单处理器，专门为并行计算进行了优化，以相同的指令对以常规模式访问的数据进行操作。每个GPU处理器有更多的算术逻辑单元（ALU），但控制逻辑减少，缓存也更小（见图1）。因此，GPU最擅长在大型数据工作集上进行高度规则和可分离的计算（例如，大型矩阵-矩阵乘法），其中大部分高速缓存（被称为共享内存）可以由程序员手动管理。我们还注意到，数据必须在CPU和GPU之间传输，产生I/O的开销。

图一： 多核CPU和GPU处理器的高层架构

我们的工作使用NVIDIA的CUDA[40]对C++的扩展，它使用线程的并行块来计算GPU上的函数。每个区块的线程都会访问一个共享的缓存，并保证在同一个处理器上运行，但区块的顺序并不保证。关于CUDA及其编程模型的更多信息，我们建议阅读NVIDIA CUDA编程指南[40]。

B. 刚体动力学

最先进的基于空间代数的刚体动力学算法[10]在最小坐标中运行，计算关节位置$q\in {\mathbb{R}}^n$、速度$\dot{q}\in {\mathbb{R}}^n$、加速度$\ddot{q}\in {\mathbb{R}}^n$和输入扭矩$\tau \in {\mathbb{R}}^m$的函数，满足：

$$M(q)\ddot{q}+C(q,\dot{q})\dot{q}+G(q)=B(q)\tau +J(q{)}^{T}F\text{\hspace{1em}(1)}$$

其中$M(q)\in {\mathbb{R}}^{n\times n}$是质量矩阵，$C(q,\dot{q})\in {\mathbb{R}}^{n\times n}$是科里奥利矩阵，$G(q)\in {\mathbb{R}}^n$是广义的引力，$B\in {\mathbb{R}}^{n\times m}$将控制输入映射为一般化的力量，最后$J(q)\in {\mathbb{R}}^{n\times p}$将任何外力或约束力$F\in {\mathbb{R}}^p$映射为广义的力。常见的算法包括：正向动力学，当给定$q、\dot{q}、\tau$和可选的$F$时，计算$\ddot{q}$；逆向动力学，当给定$q、\dot{q}、\ddot{q}$和可选的$F$时，计算$\tau$；以及方程1中的各种项的计算。

在计算过程中，空间代数将大多数数量表示为对$R^6$中的向量和$R^{6\times 6}$中的矩阵的操作，这些都是在每个刚体的框架中定义的。这些框架被编号为$i=1$到$n$，这样每个体的父体${\lambda }_i$是一个较低的数字。大多数刚体动力学算法通过在这些框架上的外向和内向循环来操作，收集和转换力、加速度、速度和惯性。从框架${\lambda }_i$到$i$的变换矩阵表示为${}^i{X}_{{\lambda }_i}$，可以从两个坐标框架之间的旋转和平移中构建，这两个坐标框架本身是这些框架之间的联合位置$q_i$和从机器人的拓扑结构中得到的常数的函数。每个环节的质量分布用其空间惯性$I_i$表示，$S_i$是一个与关节有关的项，表示一个关节可以在哪些方向移动（通常是一个常数）。最后，空间代数使用空间交叉积算子$\times$和${\times }^{\ast }$，其中一个向量被重新排序为一个矩阵，然后进行标准的矩阵乘法。对于一个向量$v\in {\mathbb{R}}^6$，这种重新排序显示在公式2中。

关于基于空间代数的刚体动力学的更多信息，我们建议阅读Featherstone的刚体动力学算法[10]。

4. GRiD库

GRiD库的开源代码可以在https://github.com/robot-acceleration/grid中找到。在这一节中，我们我们描述了它的设计、特性和代码优化方法。

A. 设计

我们的首要设计方法是使GRiD容易被其他机器人研究人员采用和扩展。

因此，优化后的CUDA C++代码被设计成只有一个头，即标准的$\mathrm{c}\mathrm{u}\mathrm{d}\mathrm{a}\_\mathrm{r}\mathrm{u}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{m}\mathrm{e}.\mathrm{h}$库。我们还提供了APIs，允许用户自动初始化和分配CPU和GPU上所有必要的内存，并将GRiD直接集成到他们现有的CUDA代码中或通过标准的CPU C++函数调用。

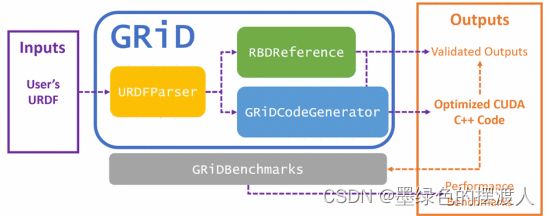
最后，GRiD库是用一套模块化的开源包建立的（如图2所示），以便于扩展，并被其他机器人研究人员重新使用。我们的GRiD软件包包装了我们的GPU代码生成引擎（GRiDCodeGenerator），一个独立的URDF解析器（URDFParser），以及一套可用于代码验证和测试的刚体动力学算法的参考实现（RBDReference）。我们还将第五节中描述的基准实验作为一个单独的包（GRiDBenchmarks）提供，因为它们需要额外的外部库支持。

图二：GRiD库包生态系统，展示了如何将用户的URDF文件转化为优化的CUDA C++代码，然后可以根据参考输出进行验证，并进行性能基准测试。

B. 当前特征

GRiD库目前完全支持任何由渐开线、棱柱线和固定关节组成的机器人模型，并实现了以下刚体动力学算法。

• 递归牛顿-欧拉算法（RNEA）用于逆动力学[10]；
• 质量矩阵的直逆（$M^{-1}$）[12]；
• 通过$-M^{-1}(\tau -\mathrm{R}\mathrm{N}\mathrm{E}\mathrm{A}(q,\dot{q},0))$的前向动力学[10]；
• 反动力学的分析梯度与机器人的位置和速度（$q$，$\dot{q}$）有关[12]。
• 通过$\frac{\partial \ddot{q}}{\partial u}=-M^{-1}\frac{\partial \mathrm{R}\mathrm{N}\mathrm{E}\mathrm{A}(q,\dot{q},\ddot{q})}{\partial u}$[12]，得出关于机器人位置、速度和输入扭矩（$q$, $\dot{q}$, $u$）的前向动力学的分析梯度。

未来的工作方向包括用额外的算法和联合类型来扩展这个核心（见第六节）。

C. 代码优化方法

GRiD建立在最近的工作基础上，该工作设计了一个手动优化的刚体动力学梯度的GPU实现，用于一个七连杆的串行链操纵器[25]。本节将详细介绍GRiD如何利用先前工作中确定的优化，以及GRiD如何扩展和概括这些优化，以便通过URDF驱动的代码生成，对更大类的机器人模型和其他刚体动力学算法进行加速。

以前的工作表明，机器人的拓扑结构和关节类型直接定义了结构化的稀疏模式和由此产生的基于空间代数的刚体动力学算法的并行机会[41], [11], [13], [25], [42]。GRiD利用独立计算之间的多线程的粗粒度并行性，以及每个计算内部的细粒度并行性。例如，在每个独立的梯度计算中，该计算的每一列都可以被并行计算。同样，在这些计算中，每个矩阵-矩阵或矩阵-向量乘法的每个条目都可以并行计算。GRiD通过使用GPU上的并行线程块，利用这种细粒度的并行性，能够实现高性能。

然而，为了让GPU有效地利用这种细粒度的并行性，以前的工作也表明，目标算法需要重构以消除同步点，并凝聚内存访问和计算操作[25]。这对空间交叉乘积操作（公式2）尤为重要，因为它导致了内存访问的失序，并将输入矢量的维度扩展为输出矩阵。我们调整了先前工作中使用的重构方法[25]，通过创建可以并行计算的临时变量，将计算从串行循环中移出。

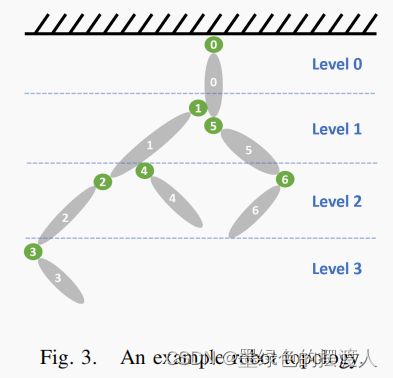
GRiD对这些产生并行性的优化进行了扩展和概括，使其能够针对任何具有分支树形拓扑结构的机器人（例如，图3）。为了做到这一点，我们注入了额外的优化，以适应树的不同层次的多个分支点。例如，由于刚体动力学算法的串行传递中的依赖关系是在树中的父框架和子框架之间，我们可以并行计算 "兄弟姐妹 "框架。例如，$\nabla \mathrm{R}\mathrm{N}\mathrm{E}\mathrm{A}$的前向传递（算法1）计算帧$i$的临时变量$\partial v_i$，$\partial a_i$是其父帧${\lambda }_i$的$\partial v_{{\lambda }_i}$，$\partial a_{{\lambda }_i}$的函数（第2和第3行）。因此，我们可以通过在树的各个层次中串行计算每个$\partial v_i$、$\partial a_i$，同时并行计算每个层次中的所有框架。对于图3所示的机器人，我们将计算与第0帧相关的值，然后并行计算1和5，然后并行计算2、4和6，最后计算3。GRiD还对这些剩余的串行循环执行循环解卷，以使编译器能够轻松优化结果代码。然后，一旦所有的$\partial v$、$\partial a$都被计算出来，所有的$\partial f$就可以被完全并行计算了。

图三：一个机器人拓扑结构的例子。

当支持任意大的机器人时，确保临时变量适合GPU缓存也很重要。在代码生成时，GRiD决定是否有必要放弃任何临时内存的计算，以支持具有许多自由度（dof）的机器人。例如，对于30个自由度的Atlas人形机器人，GRiD不会并行计算每个$v\times$矩阵，然后使用线程矩阵乘法（如以前的工作[25]），而是在几个并行线程中计算$v_1\times v_2$，用轻微的延迟惩罚换取大量共享内存的使用。这就产生了算法2中所示的经过重构的$\nabla \mathrm{R}\mathrm{N}\mathrm{E}\mathrm{A}$算法的前向传递。

GRiD还利用机器人的拓扑结构来确定梯度计算所需的许多临时变量的稀疏性模式。因此，将跳过全部为零的临时内存变量列，并对共享内存进行压缩以有效删除这些列。对于大多数机器人模型来说，这导致了显著的节约。例如，四足机器人HyQ[43]的共享内存用量减少了60%以上（大多数所需的内存偏移量都是在代码生成时计算和缓存的。GRiD采用了非分支的$if/else$结构（例如，$\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{u}\mathrm{l}\mathrm{t}=\mathrm{f}\mathrm{l}\mathrm{a}\mathrm{g}\ast \mathrm{v}\mathrm{a}\mathrm{l}1+!\mathrm{f}\mathrm{l}\mathrm{a}\mathrm{g}\ast \mathrm{v}\mathrm{a}\mathrm{l}2$），以避免任何其他指针偏移或控制流切换的分支性能惩罚。）。

最后，GRiD对某些类别的机器人模型采用了进一步的优化。例如，对于所有的单链机器人，父方的帧号总是比子方的少一个。对于这些机器人，GRiD生成的代码将删除对父（或子）帧号的任何间接引用，而是简单地减去（或增加）一个。

GRiD将类似的重构模式、内存压缩和计算优化应用于IV-B节中描述的所有算法。

5. 性能基准

我们将GRiD库与Pinocchio库[13]（我们使用了pinocchio3-preview分支的最新优化代码。）进行比较，后者是最先进的刚体动力学的CPU实现，支持刚体动力学及其分析梯度的优化CPU代码生成。这个评估的源代码可以在以下网址找到:
https://github.com/robot-acceleration/GRiDBenchmarks

A. 方法

我们使用了一台高性能的工作站，它配备了3.8GHz的八核英特尔酷睿i7-10700K CPU和1.44GHz的英伟达GeForce RTX 3080 GPU，运行Ubuntu 20.04和CUDA 11.4 （为了在CPU上进行干净的时间测量，我们禁用了TurboBoost，并将时钟频率固定为最高。代码是用Clang 12和g++9.4编译的，时间是用Linux系统调用clock_gettime()测量的，使用CLOCK_MONOTONIC作为源。）。我们比较了三种机器人模型的计时结果：7自由度（dof）的库卡LBR IIWA-14机械手[44]，12自由度的HyQ四足动物[43]，以及30自由度的Atlas人形机器人[45], [46]。对于单次计算和多次计算的延迟，我们分别取了一百万次和十万次试验的平均值。

B. 多重计算延时

为了描述我们在典型的非线性轨迹优化场景中的性能，其中使用了数十到数百个动力学算法的自然并行计算，我们在图4中评估了使用Pinocchio和GRiD对机器人模型进行的$N=16、32、64、128和256$的前向动力学梯度计算的延迟情况。这些时间被分解为CPU或GPU上的计算时间和GPU的I/O开销。图中叠加了GRiD与Pinocchio相比在纯计算方面的提速（或减速），以及包括I/O开销的提速。我们使用前向动力学的梯度作为我们的代表内核，因为它使用许多其他内核作为子程序，是计算强度最高的内核，清楚地显示了扩展趋势。

图四：在Pinocchio CPU基线和GRiD GPU库对各种机器人模型（IIWA、HyQ和Atlas，如第V-A节所述）进行N=16、32、64、128和256的前向动力学梯度计算的延迟（包括GPU I/O开销）。叠加的是GRiD与Pinocchio相比，在纯计算和包括I/O开销方面的加速（或减速）。

除了一项多重计算延迟测试外，GPU在其他所有测试中都优于CPU，即使考虑到I/O。在CPU更快的一项测试中–包括I/O在内的计算量最少的IIWA（最小的只有一个肢体的机器人），GPU的速度仍然是0.9倍。

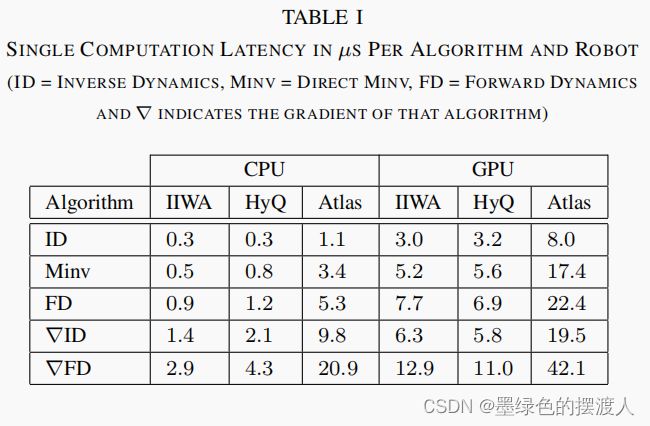
即使在CPU上，这个基准也显示了利用计算之间的粗粒度并行的优势是多么重要。例如，前向动力学内核的梯度（表I中的$\nabla FD$）在IIWA，HyQ和Atlas的单次计算中分别需要2.9，4.3和20.9微秒。如果我们连续运行256次，将花费超过742，1091和5355微秒。如图4所示，在8核上并行计算只需要123、172、865微秒，节省了83-84%的计算时间。

然而，由于CPU只有8个内核，它无法有效地扩展以利用大量的自然并行计算，与IIWA、HyQ和Atlas的N=16相比，N=256的计算时间分别为5.4倍、6.2倍和11.8倍。

另一方面，GPU的设计是通过为每个计算启动独立的线程块来扩展到更高的计算数量而不产生延迟惩罚。事实上，对于IIWA和HyQ，N=256只需要N=16的1.3倍和1.5倍时间。这导致GPU在N=256的情况下比CPU多出5.3倍和7.2倍，在包括I/O的情况下保持2.5倍和2.1倍的速度。

对于高得多的Atlas机器人，在N=256的情况下，GPU仍然比CPU高出5.0倍，如果包括I/O，则高出2.0倍。然而，与IIWA和HyQ不同的是，这一性能提升与N=128和N=64时的提升几乎相同。这种性能提升的停滞是由Atlas的30 dof所需的大量共享内存造成的，这开始限制了GPU硬件上可以同时容纳的平行线程块的数量。

最后，我们注意到，对于GPU来说，在N=256的情况下，I/O开销占到总时间的53-71%。这表明，如果将GRiD直接集成到一个完全基于GPU的算法中，而不是用来加速基于CPU的算法的一个步骤，那么GRiD可以提供最高的性能。然而，在这两种情况下，如果有足够的并行工作要做，GRiD可以减少整个计算延迟。

C. 单一计算延时扩展

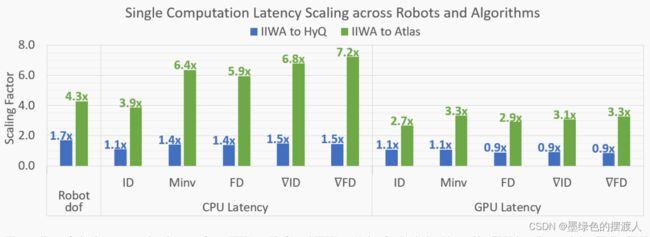
为了进一步分析第V-B节中展示的GPU性能优势，我们在图5中绘制了从IIWA到HyQ和IIWA到Atlas的每种刚体动力学算法在CPU和GPU上的单一计算的延迟扩展，不包括I/O开销，并在表I中列出了绝对时间。我们还绘制了机器人的缩放比例，作为衡量其计算复杂性的标准。

我们发现，通过利用独立的机器人肢体和梯度计算的独立列所引起的细粒度并行性，GPU能够比CPU更好地扩展到更复杂的机器人和算法。正如预期的那样（与以前的工作[25]一致），GPU在单次计算上比CPU慢，但GPU在算法和机器人复杂度上都表现出更好的可扩展性。例如，如表I所示，对于$\nabla FD$，CPU比GPU快4.4倍（2.9µs vs. 12.9µs），但对于Atlas只快2.0倍（20.9µs vs. 42.1µs）。也就是说，在所有单独的计算中，CPU仍然比GPU快，这表明GPU加速只有在有足够的并行工作要做的时候才有意义。

在CPU上，每种算法的延迟直接与它的计算强度成正比，梯度需要明显更多的计算（见表一）。计算强度最大的算法，正向动力学梯度（$\nabla FD$），在IIWA，HyQ和Atlas中需要2.9，4.3和20.9μs，而最简单的算法，逆向动力学（ID）需要0.3，0.3和1.1μs–9.7倍到19.0倍的延迟。

CPU的延迟也会随着机器人的摇摆度而变化（图5）。例如，从IIWA到HyQ，机器人的齿数增加了1.7倍，计算时间也增加了1.1倍，对于$O(N)ID$算法，对于$O(N^2)\nabla FD$算法，增加了1.5倍。似乎这种强大的性能是由于代码生成利用了梯度中的许多共享计算，以及HyQ的独立肢体所引起的稀疏性，这使得通过刚体树的最长路径从IIWA的7条减少到HyQ的3条。然而，这些优化被Atlas模型缓解了，它有一个更大的30 dof，通过刚体树的最长路径为8。Atlas有4.3倍于IIWA的dof，但在CPU上有3.9倍$（ID）$到7.2倍$（\nabla FD）$的减速。

图五：在Pinocchio CPU基线和GRiD GPU库中，各种刚体动力学算法（ID=逆向动力学，Minv=直接Minv，FD=正向动力学，∇表示该算法的梯度）的单一计算延迟从IIWA到HyQ和IIWA到Atlas的比例。我们还绘制了机器人的缩放比例，作为衡量其复杂性增加的一个标准。

相比之下，GPU不仅能够利用稀疏性和共享计算来提高其可扩展性，而且还能利用复杂机器人模型中的独立肢体和梯度计算的独立列造成的细粒度并行的机会。例如，表I显示，通过利用梯度计算中的并行性，GPU不仅能够比$FD$更快地计算$\nabla ID$，而且只需要12.9，11.0和42.1微秒（对于IIWA，HyQ，Atlas），而ID只需要3.0，3.2和8.0微秒–速度只下降了3.4倍到5.3倍，与CPU的9.7倍到19.0倍的速度相比，这些算法的速度明显降低。同样，图5显示，通过利用基于肢体的并行性，GPU计算HyQ的前向动力学$（FD）$和两个梯度$（\nabla ID，\nabla FD）$的速度比IIWA快，而且从IIWA到Atlas只有2.7倍到3.3倍的减速，同样比CPU的3.9倍到7.2倍有明显减少。

6. 结论和未来工作

在这项工作中，我们介绍了GRiD，一个具有分析梯度的GPU加速的刚体动力学库。我们发现，在对刚体动力学算法进行多次计算时，通过利用大规模的并行性，GRiD可以比最先进的多线程CPU实现提供多达7.2倍的速度，并且在包括I/O开销时保持多达2.5倍的速度。

未来的工作有许多有希望的方向，以扩展GRiD库的功能和多功能性。我们目前正在开发的工作是扩展GRiD，以支持目前最先进的基于CPU空间代数的刚体动力学库所支持的全部刚体动力学算法和机器人模型[26], [11], [13], [27], [28]。此外，我们正在开发更高级别的语言对我们的C++主机函数的封装，以使其更容易利用GRiD。

我们希望探索新兴的刚体动力学算法，以及刚体动力学的替代公式和实现，这可能通过暴露额外的并行性和计算效率来提高整体性能[47]、[48]、[49]、[50]、[51]、[52]、[53]、[54]、[55]。

我们还希望增加对通过模型参数[56]、[57]以及接触的支持，并希望将这些加速动力学的实现整合到现有的机器人软件框架中[58]、[59]、[60]、[16]、[61]。这将增加GRiD的易用性和对更多机器人研究者的适用性。

最后，为更多完全在GPU上运行的轨迹优化、MPC和ML算法建立更多的支持，将进一步提高将GRiD集成到这些方法中的性能优势。