简述基于PyTorch框架的卷积神经网络（Convolutional Neural Network，CNN）

PyTorch框架使得构造和训练神经网络方便了许多，为简述其用法，同时也为说明卷积神经网络的原理，本文举例说明如何基于PyTorch框架构造并训练一个卷积神经网络用于识别手写阿拉伯数字。

一、卷积神经网络简介

（一）什么是卷积神经网络

卷积神经网络（Convolutional Neural Network，CNN）本质上仍是一堆激活函数的线性组合。与原始BP网络（详见《详解反向传播神经网络》）所不同的是BP网络为前一层的每个输出神经元到后一层的每个输入神经元都设置了一个独享的权重值，且后一层各神经元的输入收到了前一层所有神经元输出的影响；而CNN则没为，一方面它采用的是权值共享，即后一层不同神经的输入会共享相同的权值组，且后一层每个神经元的输入只受前一层部分神经元输出的影响。这样做的好处的避免纠缠不必要的细节，而是尽量抽象出整体特征，这点十分适用于图像识别。

一张黑白图片可视为一个数值矩阵，矩阵中的每个数值代表该位置的像素亮度；一张彩色图片可视为三个同尺寸数值矩阵，即三个图层,各图层矩阵中的数值分别代表该位置像素的RGB（红色、绿色、蓝色）亮度值。当然，任何一组信号也可以视为一副图像，每个分量信号值都可视为一个像素，后文为方便描述，将CNN的每个入参都称为一个像素。

最早的CNN模型一般可追溯到1989年由图灵奖得主LeCun Yann教授提出的LeNet模型。该模型设置了一系列卷积、激活、池化操作，在此过程中，输入图像的尺寸变得越来越小，图层变得越来越多，从而实现特征提取，识别图像内容。如下图所示：

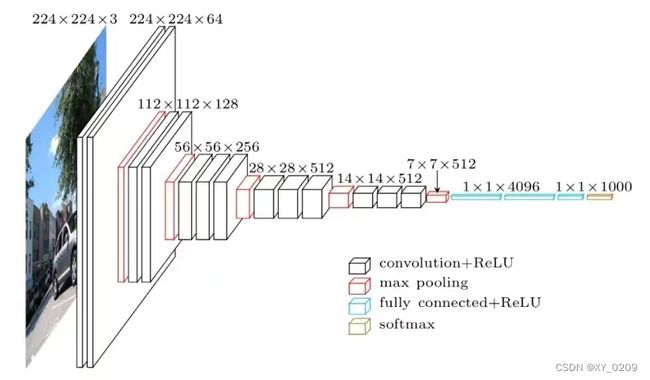
（二）卷积神经网络的结构

如果仍将激励函数视角为一个神经元的主体，处于同一次序上的一批神经元视为一层神经元，则CNN就是在普通BP神经元层前面增加了几个卷积神经元层。这些卷积层的神经元除了会共享权值外，还会在各输入信号经过激活函数后将一部分相邻神经元的输出信号做池化处理，即归并成一个输出。下面就分别具体讲一些这些卷积层神经元的三项工作：

1. 卷积。前面提到被共享的权值被称为卷积核。即每个图层上的一个权值矩阵，一般用一个尺寸为$k\ast m\ast n$的三阶张量表示。其中，$k$为输入图层数，$m\ast n$为每个图层上的权值矩阵尺寸。卷积的过程就是使卷积核以一定步长在各输入图层上由左至右由上至下（或者先上下后左右都无所谓）的平移，每平移一步，就用卷积核的各权值与各对应位置上的像素值做加权求和，得到一个卷积输出值放在当前平移的位置。以单图层输入为例，一个尺寸为$3\ast 3$的卷积核以1个像素为步长做卷积过程如下图所示：
   
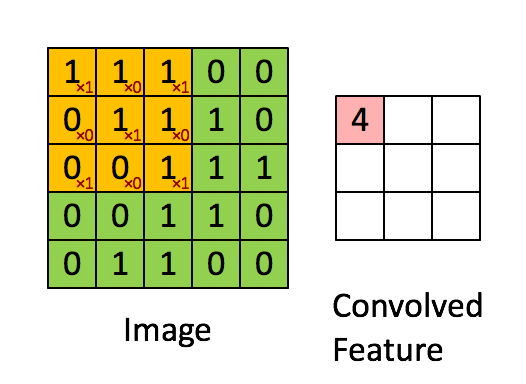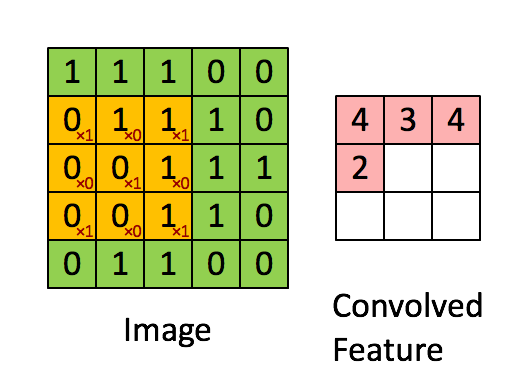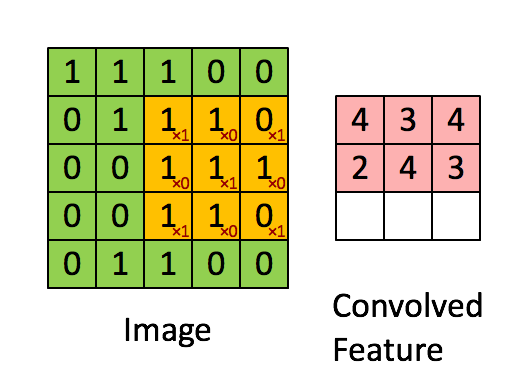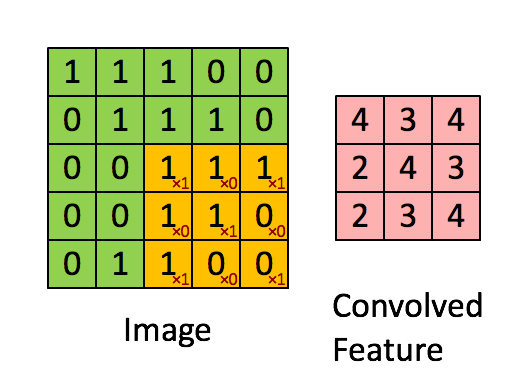
   可见，一个卷积核的卷积结果是一个图层，因此有几个卷积核，就会卷积得到几个图层。类同于BP网络，每个卷积后图层各像素值还会都再加一个相同的偏置量，即对于一个卷积神经元层，需要训练的网络参数除了每个卷积核中权值外，还有每个卷积核对应的一个偏置量。
2. 激活。卷积后的各图层像素相当于该卷积层各神经元的输入，同样会分别经一个相同的激活函数做映射，映射出的图层数和尺寸都不会改变。此激活函数的网络创建时就既定的，无需训练。
3. 池化。为了压缩卷积激活后的各输出图层中的关键特征信息，类似于卷积操作，只不过此时没有卷积核，按一定步长将每个图层划分成等尺寸的一个个方阵，再将每个方阵中的所有像素以某种算法（如取最大值或取平均值）映射成一个像素，如下图所示：
   
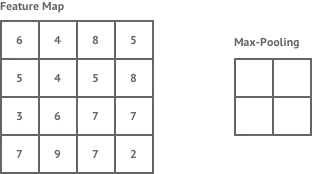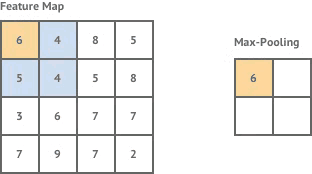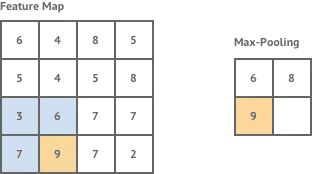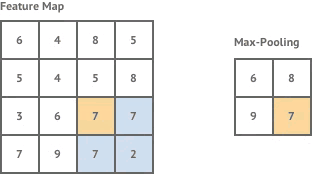
   可见，池化操作会使得各图层的尺寸变小，图层数不变。池化操作选择的具体算法同样也是在网络创建时既定的，无需训练。

所谓张量，可以简单理解为多维数组。比如一个数字是0阶张量；一组数字构成一个向量，就是1阶张量；一组同尺寸的向量构成一个矩阵，就是2阶张量；一组同尺寸的向量构成一个矩阵，就是3阶张量；一组同尺寸的3阶张量构成一个4阶张量，以此类推。

（三）为何要用卷积神经网络

其实单纯用原始BP网络也可以实现图像识别的效果，但需要训练的网络参数要远远多于CNN的网络参数。

以一幅$100\ast 100$像素的黑白图像为例，假设使用的BP网络含3个隐含层1个输出层，各隐含层神经元个数也是$100\ast 100$，输出层含3个神经元。则涉及的待训练参数包括各层神经元的权重矩阵及偏移量，有$3\ast (10000^2+10000)+30003=300060003$个。

而如果将这三个隐含BP层都改为卷积层，假设所有卷积核尺寸都是$3\ast 3$，池化尺寸都是$2\ast 2$，假设第一个卷积层有10个卷积核，则待训练参数有$(3\ast 3+1)\ast 10=100$个，池化后图像含有10个图层，每个图层长宽尺寸都缩小一般，即变为一个$10\ast 49\ast 49$的三阶张量；设第二个卷积层有20个卷积核，则待训练参数有$(3\ast 3\ast 10+1)\ast 20=1820$个，池化后图像变成一个$20\ast 24\ast 24$的三阶张量；设第三个卷积层有30个卷积核，则待训练参数有$(3\ast 3\ast 20+1)\ast 30=5430$个，池化后图像变成一个$30\ast 11\ast 11$的三阶张量；假设后面再跟两个BP层，分别有100个神经元和3个神经元，对应的待训练参数分别有$(11\ast 11\ast 30+1)\ast 100=363100$个和$(100+1)\ast 3=303$个。则整个CNN一共需要训练的网络参数有$100+1820+5430+363100+303=370753$个。远远小于纯BP网络的3亿多个待训练参数。

二、PyTorch框架简介

对于有监督学习的神经网络模型，其模型训练过程基本都是通过梯度下降来实现的。即把整个网络模型视为一个由所有待训练参数（各权重值和偏置值）作为自变量，由损失（体现模型输出与目标值直接的差异）作为函数值的多元函数，求得该多元函数在当前自变量坐标处的梯度，就可以沿此梯度的反方向对当前自变量坐标做一小步调整，即完成了一次训练。可见，训练神经网络的关键，也是最消耗算力的地方就是时刻要计算多元函数梯度，而这项工作在PyTorch框架中可以很容易的完成。

（一）环境搭建

PyTorch是个第三方库，原装的Python自身并没有，需要下载安装，但不能像“numpy”这类第三方库那样直接pip，因为要根据你的本地环境选择具体要下载安装的包，因此要先登录“https://pytorch.org/”网址，找到下图位置：

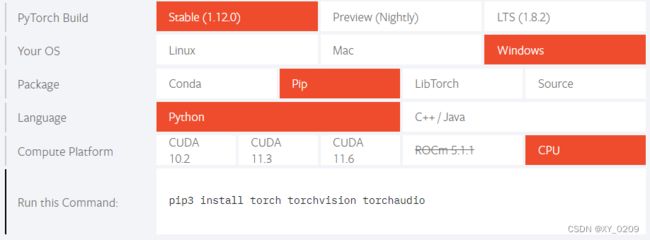
在这里选择想要的PyTorch的版本、你本地的操作系统（如Windows）、使用的下载方式（如pip）、使用的编程语言（如Python），以及使用的计算设备，如果本地有GPU（可通过设备管理器查看显卡资源，有一个是集成显卡，没有GPU；有两个才是独立显卡，有GPU），可以根据本地显卡配置选择具体显卡型号（如CUDA11.6）来获取一个使用GPU做运算的PyTorch包，从而有效提高运算速度；如果本地没有显卡，则计算设备就选择CPU。当上述选项都选择好后，上图的最后一行会给出一行命令，直接复制该命令到命令窗（如Anaconda Prompt）运行即可。但由于PyTorch包较大，而其源服务器又在国外，下载速度较慢，可以改为从国内源下载来有效提高下载速度，常用的国内源有以下这些：

1. 阿里云： https://mirrors.aliyun.com/pypi/simple/
2. 豆瓣：http://pypi.douban.com/simple/
3. 清华大学：https://pypi.tuna.tsinghua.edu.cn/simple/
4. 中国科学技术大学：http://pypi.mirrors.ustc.edu.cn/simple/
5. 华中科技大学：http://pypi.hustunique.com/

只需要在原"pip install"命令后插入“-i + 某一源的地址”，后面的命令内容不变，如清华源：“-i https://pypi.tuna.tsinghua.edu.cn/simple”。完成安装后即可导入该框架下的一些包，如torch、torchvision等。

（二）一些基本概念和应用

在PyTorch框架中的一个核心数据类型是前面提到的张量，即Tensor。伴随此数据类型的核心操作是梯度计算。下面将逐一说明与之相关一些基本概念和代码操作。

1. 张量的创建

import torch
import numpy as np

t0 = torch.zeros(5, 3, 2)                          #各元素用0填充
t1 = torch.ones(5, 3, 2)                           #各元素用1填充
tr = torch.randn(5, 3, 2)                          #各元素用标准正态分布随机数填充
lis2t = torch.tensor([[1,2],[3,4],[5,6]])          # 直接由列表数据构造张量
ta = torch.arange(12.0)                            # 由浮点型序列构造张量
arr2t = torch.tensor(np.array([[1,2],[3,4]]))      # 将np数组转化成张量
mat2t = torch.tensor(np.matrix([[1,3],[3,5]]))     # 将np矩阵转换成张量
t2mat = np.matrix(mat2t)                           # 将张量转换成np矩阵
t2arr = np.array(arr2t)                            # 将张量转换成np数组

2. 张量的属性

s0 = t0.shape                                      # 张量的形状
device0 = t0.device                                # 张量的运算设备（如GPU或CPU）
print(t0.requires_grad)                            # 当前张量是否会被视为自变量来计算梯度
print(t0.is_leaf)                                  # 当前张量是否为叶子节点（即手创或由“不计算梯度”张量运算出的张量）
print(t0.grad_fn)                                  # 生成当前张量的生成函数（凡叶子节点的生成函数都为None）

之所以要标注一个张量是否为叶子节点，就是要告诉系统在自动计算多元函数梯度时，哪些变量才是要作为函数梯度的一个维度的自变量，哪些变量只是函数中的参数。

3. 张量的使用

ele = tr[0][1][1].item()                           # 取张量中的一个元素。注意：只有标量才能取其值
tta = ta.reshape(2, 2, 3)                          # 更改张量形状，但元素数要与原张量一致
arr2ft = arr2t.float()                             # 将张量中各元素类型转为浮点型，许多张量运算只适用于浮点型
y1 = arr2ft * mat2t                                # 得到两张量的对应元素乘积
y2 = arr2ft @ arr2ft                               # 对2阶张量（矩阵）做点积
y3 = torch.t(arr2t)                                # 对2阶以下张量求其转置
y4 = torch.inverse(arr2ft)                         # 对2阶张量求其逆张量（张量中元素必须是浮点型）
m2 = y2.mean()                                     # 求张量中各元素均值（也只适用于浮点型元素）

4. 张量的梯度计算

arr2ft.requires_grad = True                        # 将要计算梯度的张量的“计算梯度”属性置为真，默认是假
yy = arr2ft @ arr2ft                               # 做矩阵乘法
yy.requires_grad                                   # “计算梯度”属性置真后算得的张量，其该属性也自动为真
print(yy.is_leaf)                                  # 由“计算梯度”张量运算出的新张量不再是叶子节点
print(arr2ft.is_leaf)                              # 手创的“计算梯度”张量是叶子节点
print(yy.grad_fn)                                  # 非叶子张量会有生成函数
fy = yy.mean()                                     # 由张量运算出标量，因为只能针对作为标量的最终函数值计算梯度
print(arr2ft.grad)                                 # 梯度计算前叶子张量的梯度属性为空
fy.backward()                                      # 利用偏导的反向传递计算各叶子张量的梯度
print(arr2ft.grad)                                 # 每次算得的梯度会累加进叶子张量的梯度属性里

在PyTorch框架中，各叶子张量无论经历怎样复杂的函数运算，这些函数也无论是库函数还是手写的，只要最终能得到一个标量函数值，都能追溯到此函数值对各叶子张量的梯度，其背后的数学原理就是多元函数的偏导计算公式。

5. 更新叶子张量后使其仍保持叶子属性
   前面提到叶子节点必须是手创或是全由“不计算梯度”的张量运算出的张量，但在神经网络训练过程中，待训练的参数张量一方面必须要设置成是“计算梯度”的，另一方面在每次训练中要被迭代更新，而这更新过程就是由原参数张量参与计算得到新参数张量，这样一来，新参数张量必然不再是叶子节点，也就无法再进行下一次训练迭代了。为解决此问题，需要设法使更新后的叶子张量仍保持其叶子属性。此时要用到Python的上下文操作：

with torch.no_grad():
    arr2ft = arr2ft - arr2ft.grad                   # 在no_grad上下文中更新叶子张量
print(arr2ft.is_leaf)                               # 此时原叶子张量虽被运算更新，但仍恢复成最初叶子属性
arr2ft.requires_grad                                # 梯度计算开关也置回默认关闭状态
print(arr2ft.grad)                                  # 梯度属性也自动清空
arr2ft = arr2ft - arr2ft.grad                       # 如果直接更新叶子张量，则会将其变为生成张量，即非叶子张量
print(arr2ft.is_leaf)

三、应用示例

基于PyTorch框架关于Tensor的这些功能，就可以很方便是手写出一些神经网络的运算和训练操作。为了进一步方便用户，PyTorch框架还提供了数据采集器、加载器、损失计算器、网络优化器，以及用于构建所有神经网络的基础类等模块，可以免去许多繁琐的重复劳动。为说明如何使用这些工具模块，下面以一个实际项目案例做说明。

（一）项目目标

识别手写的0~9阿拉伯数字。

（二）准备样本

此例的样本准备很简单，就是手写了几遍（我写了6遍）0~9这十个数字，然后拆分两半，30个数字图片放入一个文件夹，命名为“train”，作为训练集；另外30个数字图片放入另一个文件夹，命名为"test"，作为测试集。每个图片文件的命名如下图所示：

然后就是在Python中创建样本的加载器：

# =============================================================================
# 初始化全局变量
# =============================================================================
BATCH_SIZE = 1                     # DataLoader每批次读取样本数
IMG_SIZE = (32, 32)                # 标准化图像尺寸
NORM_MEAN = [0.485, 0.456, 0.406]  # Image-net大赛中使用的图像数据均值
NORM_STD = [0.229, 0.224, 0.225]   # Image-net大赛中使用的图像数据标准差
LR = 0.05                          # 网络的学习率，即迭代步长
MOMENTUM = 0.2                     # 网络学习动量，即在每次训练中保持此比例的参数不变
MAX_EPOCH = 60                     # 最大训练轮数，一轮是把所有训练样本跑一遍

# =============================================================================
# 准备样本数据
# =============================================================================
from torch.utils.data import Dataset
from torch.utils.data import DataLoader
from PIL import Image
import os
from torchvision.transforms import transforms
import torch

# 编码器
encoder = {
        "0":torch.tensor([1.,0.,0.,0.,0.,0.,0.,0.,0.,0.]),
        "1":torch.tensor([0.,1.,0.,0.,0.,0.,0.,0.,0.,0.]),
        "2":torch.tensor([0.,0.,1.,0.,0.,0.,0.,0.,0.,0.]),
        "3":torch.tensor([0.,0.,0.,1.,0.,0.,0.,0.,0.,0.]),
        "4":torch.tensor([0.,0.,0.,0.,1.,0.,0.,0.,0.,0.]),
        "5":torch.tensor([0.,0.,0.,0.,0.,1.,0.,0.,0.,0.]),
        "6":torch.tensor([0.,0.,0.,0.,0.,0.,1.,0.,0.,0.]),
        "7":torch.tensor([0.,0.,0.,0.,0.,0.,0.,1.,0.,0.]),
        "8":torch.tensor([0.,0.,0.,0.,0.,0.,0.,0.,1.,0.]),
        "9":torch.tensor([0.,0.,0.,0.,0.,0.,0.,0.,0.,1.]),
        }

class NumDataset(Dataset):
    '''
    用于读取图像数据，包括训练数据和测试数据，并按指定方式（如有）做数据转换。
    
    Parameters of init
    ----------
    dataDir : String
        给出相对当前PYTHONPATH目录的数据地址。
    transformer : 
        图像数据转换器，包含了对图像数据需要做的一些转换。默认为空。
    '''
    def __init__(self, dataDir, transformer=None):
        self.dataInfo = []      # 初始化一个图像数据信息元组列表
        # 遍历每个图片文件名
        for item in os.listdir(dataDir):
            label = item[1]     # 每张图片文件名的第二个字符为该图片的标签
            imgPath = dataDir + "/" + item  # 拼装成具体图片文件的地址
            self.dataInfo.append((imgPath, label)) # 一个图片地址对应其标签形成一个元组
        self.transformer = transformer
        
    def __getitem__(self, index):
        '''
        根据索引来获取一条具体数据的魔法。设有该类对象nd，运行nd[index]时即运行此魔法。
        
        Parameters
        ----------
        index : int
            代表数据元组列表种的序号。
        
        Returns
        ----------
        img : Image(default)
            代表该条图片的RGB数据。具体变量类型可能会由数据转换器改变。
        encoder[label] : Tensor
            代表该条图片数据对应的标签编码结果。
        '''
        imgPath, label = self.dataInfo[index]    # 按序号获取图片地址和标签
        img = Image.open(imgPath).convert('RGB') # 按路径获取图片RGB数据
        if self.transformer is not None:
            img = self.transformer(img)          # 用指定方式对图像数据做转换
        
        return img, encoder[label]
    
    def __len__(self):
        '''
        使得“len(该类对象)”可以正常运行。
        '''
        return len(self.dataInfo)

# 指定样本目录
sampleRootDir = "./numberSample"                  # 指定样本根目录
trainDir = sampleRootDir + "/" + "train"          # 指定训练样本目录
testDir = sampleRootDir + "/" + "test"            # 指定测试样本目录

# 指定图像数据转换方式
transformer = transforms.Compose([
        transforms.Resize(IMG_SIZE),              # 将图片大小固定为32*32像素
        transforms.ToTensor(),                    # 转化成Tensor类型数据
        transforms.Normalize(NORM_MEAN, NORM_STD) # 对图像数据归一化
        ])

# 实例化数据集
trainData = NumDataset(trainDir, transformer)     # 实例化训练数据集对象
testData = NumDataset(testDir, transformer)       # 实例化测试数据集对象

# 实例化数据加载器
trainLoader = DataLoader(                         # 训练数据加载器
        dataset = trainData,                      # 指定读取的数据集
        batch_size = BATCH_SIZE,                  # 指定每批次读取样本数
        shuffle = True                            # 打乱样本顺序
        )
testLoader = DataLoader(                          # 测试数据加载器
        dataset = testData,                       # 指定读取的数据集
        batch_size = BATCH_SIZE,                  # 指定每批次读取样本数
        shuffle = True                            # 打乱样本顺序
        )

当然你也可以不用数据加载器，在后面的网络训练中手动对各训练样本图片做格式转换，手动指出训练样本去哪取、如何取、取多少等信息。

（三）构造卷积神经网络

# =============================================================================
# 构造卷积神经网络
# =============================================================================
import torch.nn as nn
import torch.nn.functional as F

class LeNet(nn.Module):
    '''
    一种卷积神经网络。
    '''
    def __init__(self):
        '''
        定义网络结构。
        '''
        # 使用其父类来初始化
        super(LeNet, self).__init__()
    
        # 构造第一个卷积层
        self.conv1 = nn.Conv2d(
                in_channels=3,   # 指定入参数据的通道数。RGB图像是三个图层，即3通道
                out_channels=6,  # 指定该卷积层的输出通道数，即该层卷积核个数
                kernel_size=5,   # 指定卷积核尺寸，此时为5*5
                stride=1         # 指定卷积步长，即每做一次卷积后，卷积核平移一个像素
                )
        '''
        1、由于2维卷积核是长宽都是5，则会使得卷积后的结果在横纵方向上都少4个像素，因此
           卷积后的各图层尺寸由原来的32*32（IMG_SIZE）变成28*28。
        2、由于卷积核个数是6，则会使卷积后的图层变成6个，即数据尺寸为28*28*6。
        3、卷积后会做激活，而激活并不改变数据尺寸。
        4、每次激活后做2*2尺寸的2步长池化，则数据尺寸变为14*14*6。
        '''
        
        # 构建第二个卷积层（使池化后图像尺寸变为5*5*16）
        self.conv2 = nn.Conv2d(
                in_channels=6,   # 指定入参数据的通道数。即上一层输出的图层数
                out_channels=16, # 指定该卷积层的输出通道数，即该层卷积核个数
                kernel_size=5,   # 指定卷积核尺寸，此时为5*5
                stride=1         # 指定卷积步长，即每做一次卷积后，卷积核平移一个像素
                )
        
        # 构建第一个全链接层（即普通BP网络的输入加权运算）
        self.fc1 = nn.Linear(
                in_features=5*5*16, # 指定入参个数。即上一个卷积池化后的图像像素数量
                out_features=120,   # 指定出参个数。
                )
        
        # 构建第二个全链接层
        self.fc2 = nn.Linear(
                in_features=120,    # 指定入参个数。即上一层出参个数
                out_features=84,    # 指定出参个数。
                )
        
        # 构建最后一个全链接层
        self.fc3 = nn.Linear(
                in_features=84,     # 指定入参个数。即上一层出参个数
                out_features=10,    # 指定出参个数。分别对应10个数字
                )
    
    def forward(self, x):
        '''
        定义网络的前向传播运算过程。
        
        Parameters
        ----------
        x : Tensor(4D)
            一个尺寸为batchsize*IMG_SIZE*3的4阶张量，代表一个批次的RGB图像数据。
        
        Returns
        ----------
        out : Tensor(2D)
            一个尺寸为batchsize*10的2阶张量，代表该批次各图像的识别结果为各数字的概率。
        '''
        # 经过两轮卷积、激活、池化
        out = self.conv1(x)         # 由第一个卷积层对入参做卷积运算
        out = F.relu(out)           # 对卷积结果做激活运算。relu(x)=max(x, 0)
        out = F.max_pool2d(         # 对激活结果做二维最大值池化
                input=out,          # 激活结果作为池化输入
                kernel_size=2,      # 池化尺寸。即在一个2*2的像素区域中取最大值
                stride=2            # 池化步长。
                )
        out = self.conv2(out)                                  # 第二轮卷积
        out = F.relu(out)                                      # 激活
        out = F.max_pool2d(input=out, kernel_size=2, stride=2) # 池化
        
        # 将当前该批次中的每个3阶张量数据展开成1阶
        out = out.view(out.size(0), -1)
        
        # 经过三层BP网络
        out = self.fc1(out)                # 经过第一层BP加权运算
        out = F.relu(out)                  # 对加权运算结果做激活
        out = self.fc2(out)                # 经过第二层BP加权运算
        out = F.relu(out)                  # 对加权运算结果做激活
        out = self.fc3(out)                # 经过第三层BP加权运算
        out = F.softmax(out, dim=1)        # 对加权运算结果做激活得到最终输出
        '''
        1、输出有10个神经元，希望的结果是识别出输入图像是数字几，则第几个神经元输出1，
           其他输出0。
        2、max函数的效果是对各输出神经元取值做比较，最大的赋1，其余赋0。但如此则无法渐
           进对比损失大小了。
        3、softmax的效果是根据各输出神经元取值大小赋予不同的概率值，原值越大概率越大，
           各输出的概率和为1。
        4、dim=1使得每组输出都排成一行。
        '''
        
        return out
      
    def initWeight(self):
        '''
        初始化网络各待训练权重值。
        '''
        # 遍历网络的各层对象
        for m in self.modules():
            if isinstance(m, nn.Conv2d):    # 如果是卷积层
                # 使用正态分布随机数对该层卷积核各权重做初始化
                nn.init.xavier_normal_(m.weight.data)
                # 使用0对该层卷积核各偏移量做初始化
                m.bias.data.zero_()
            elif isinstance(m, nn.Linear):  # 如果是全连接层
                # 使用标准正态分布随机数对该层卷积核各权重做初始化
                nn.init.normal_(m.weight.data, mean=0, std=0.1)
                # 使用0对该层卷积核各偏移量做初始化
                m.bias.data.zero_()
            
# 实例化网络对象，并初始化网络参数
net = LeNet()
net.initWeight()

（四）训练并保存网络

# =============================================================================
# 训练并保存网络
# =============================================================================
import torch.optim as optim

# 实例化交叉熵损失计算器
losses = nn.CrossEntropyLoss()
'''
交叉熵损失函数：
CrossEntropyLoss = -1/N sum_i(sum_c=1^M(y_ic*log(p_ic)))
其中，N为样本数量；M为分类数；y_ic表示如果第i个样本属于c类，则为1，否则为0；p_ic表示预
测第i个样本属于c类的概率。
'''

# 实例化优化器
optimizer = optim.SGD(
        params=net.parameters(), # 指定网络所有参数（包括各权重和偏置）为待优化参数
        lr=LR,                   # 指定网络的学习率
        momentum=MOMENTUM,       # 学习动量，即每次训练中保持此比例的参数值不变
        )

# 开始训练
epoch = 0                        # 初始化训练轮数
while epoch < MAX_EPOCH:
    
    net.train()                  # 将网络切换到训练模式
    
    totalSampleNum = 0           # 初始化总训练样本个数
    correctSampleNum = 0         # 初始化识别正确的样本个数
    
    # 逐批次训练
    for i, data in enumerate(trainLoader):
        '''
        i ：训练批次号。
        data : 一批次的训练数据，即一批Dataset。
        '''
        
        # 获取当前批次的训练数据
        img, label = data
        '''
        img : 由各Dataset中的img构成的四阶张量。
        label : 由各Dataset中的label构成的一个元组。
        '''
        totalSampleNum += label.shape[0]   # 更新总样本个数
        
        # 获取当前这批训练数据的网络运算结果
        output = net(img)
        '''
        1、等价于net.forward(img)，且仅等价于调用"forward"这个函数名。
        2、各运算结果是一个含十个元素的张量，其和为1。
        '''
        # 输出概率最大的那个神经元位置即为识别的数字值
        res = torch.max(output.data, 1).indices         # 网络识别结果
        real = torch.max(label.data, 1).indices         # 真实结果
        correctSampleNum += (res == real).sum().item()  # 更新识别正确的样本个数

        # 计算该批训练结果的总交叉熵损失
        loss = losses(output, label)
                
        # 网络（各待优化参数）梯度清零
        net.zero_grad()
        
        # 反向传播重新生成网络梯度
        loss.backward()
        
        # 按梯度下降方向更新网络参数
        optimizer.step()
    
    # 统计该轮训练效果
    print(f"第{epoch}轮的训练准确率为{correctSampleNum/totalSampleNum}")
    
    epoch += 1

# 保存网络
torch.save(net.state_dict(), './numberSample/trainedCNN.pth')

（五）加载并使用网络

checkpoint = torch.load('./numberSample/trainedCNN.pth') # 实例化加载点
mynet = LeNet()                                          # 实例化一个LeNet
mynet.load_state_dict(checkpoint)                        # 从加载点加载网络参数
print(mynet)                                             # 查看网络结构

# 逐批次测试
totalTestNum = 0                                    # 初始化总测试样本个数
correctTestNum = 0                                  # 初始化识别正确的样本个数
for i, data in enumerate(testLoader):
    '''
    i ：测试批次号。
    data : 一批次测试数据。
    '''
    
    img, label = data                               # 获取当前批次的测试数据
    output = mynet(img)                             # 得到网络输出
    res = torch.max(output.data, 1).indices         # 网络识别结果
    real = torch.max(label.data, 1).indices         # 真实结果
    totalTestNum += label.shape[0]                  # 更新总测试样本个数
    correctTestNum += (res == real).sum().item()    # 更新识别正确的测试样本个数
    print(f"真实数字为{real}")                       # 打印当前样本真实数字
    print(f"网络识别为{res}")                        # 打印当前识别结果
    print("***********")

# 打印测试统计结果
print(f"测试准确率为{correctTestNum/totalTestNum}")