学习笔记 - GreedyAI - DeepLearningCV - Lesson3 Deep-Neural-Network

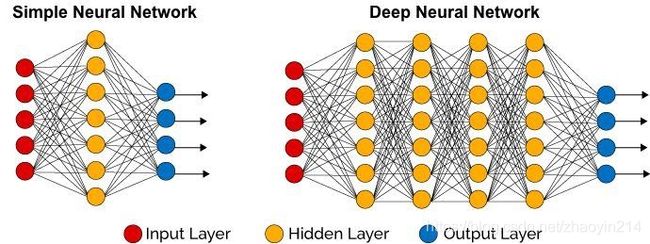
第7章 深度神经网络

任务学习41: 梯度消亡

• 深度神经网络面临的挑战

（1）梯度消亡（Gradient Vanishing）：训练过程非常慢

（2）过拟合（Overfitting）：在训练数据集上表现好，在实际测试数据集上表现差

• 梯度消亡（Gradient Vanishing）现象

（1）神经网络中，靠近输入端网络各层的系数逐渐不再随着训练而变化，或者变化非常缓慢

（2）网络层数越多，该现象越明显

• 梯度消亡(Gradient Vanishing)前提

（1）使用基于梯度的训练方法（例如梯度下降法）

（2）使用的激活函数的输出值域范围远小于输入值域范围，例如逻辑函数（logistic or sigmoid），双曲正切（tanh）

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

def sigmoid(x):
    return 1 / (1 + np.exp(-1 * x))

def tanh(x):
    return (np.exp(x) - np.exp(-1 * x)) / (np.exp(x) + np.exp(-x))

x = np.linspace(-10, 10, 100)

fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(x, sigmoid(x), label="sigmoid")
ax.plot(x, tanh(x), label="tanh")
ax.grid(True)
ax.legend()
plt.show()

任务学习42: 梯度消亡问题分析

Sepp Hochreiter（Germany）于1991年系统分析了ྛ梯度消亡的原因， 他也是LSTM的发明⼈

• 梯度消亡问题分析

梯度下降法依靠理解系数的微小变化对输出的影响来学习网络的系数。

如果一个系数的微小变化对网络输出没有影响或者影响极小，那就无法知晓如何优化这个系数，或者优化特别慢，造成训练的困难。

• 梯度消亡原因

使用梯度下降法训练神经网络，如果激活函数具有将输出值域范围相对于输入值域大幅度压缩的特性，那么就会出现梯度消亡。

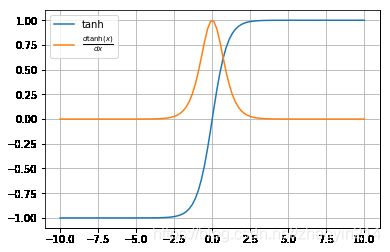
例如，双曲正切函数将$-\infty$到$+\infty$的输入压缩到$-1$到$+1$之间。除了输入在$(-3,+3)$之间的值之外，其它输入值对应的梯度都非常小，接近$0$，

def derivative_tanh(x):
    return 1 - np.tanh(x) ** 2

x = np.linspace(-10, 10, 100)

fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(x, tanh(x), label="tanh")
ax.plot(x, derivative_tanh(x), label=r"$\frac{d \mathrm{tanh}(x)}{d x}$")
ax.grid(True)
ax.legend()
plt.show()

任务学习43: 梯度消亡解决方案

• 梯度消亡解决方案

（1）激活函数ReLU：$f(x)=\max (0,x)$

输入大于$0$，梯度为$1$，否则为$0$。

$$f(x)=\{\begin{array}{ll}0,& x<0\\ x,& x\ge 0\end{array},f^{\prime }(x)=\{\begin{array}{ll}0,& x<0\\ 1,& x\ge 0\end{array}$$

（2）激活函数LeakyReLU：$f(x)=\max (ax,x),0<a<1$

输入大于等于$0$，梯度为$1$，否则为$a$。

def relu(x):
    y = x.copy()
    y[x < 0] = 0
    return y

def derivative_relu(x):
    y = np.ones(x.shape)
    y[x < 0] = 0
    return y

x = np.linspace(-5, 5, 50)

fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(x, relu(x), label="ReLU")
ax.plot(x, derivative_relu(x), ".",
        label=r"$\frac{d \mathrm{ReLU}(x)}{d x}$")
ax.grid(True)
ax.legend()
plt.show()

• 梯度消亡思考

为什么不选择激活函数：$f(x)=x$？

假设$l$层神经网络，权值矩阵分别为：${\mathbf{W}}_1,{\mathbf{W}}_2,\cdots ,{\mathbf{W}}_l$，则网络输出向量$\mathbf{y}$可表示为：

$$\begin{array}{rl}\mathbf{y}=& f\left({\mathbf{W}}_{l}f\left(\cdots f\left({\mathbf{W}}_{2}f\left({\mathbf{W}}_1\mathbf{x}\right)\right)\right)\right)\\ =& {\mathbf{W}}_l\cdots {\mathbf{W}}_2{\mathbf{W}}_1\mathbf{x}\\ =& \mathbf{W}\mathbf{x}\end{array}$$

即网络等效为单层网络，是-个线性系统，仅具有线性表示能力。

• 梯度消亡解决方案

采用不基于梯度的网络训练方法：[Derivative-tree optimization: a review of algorithms and comparison of software implementations](https://link.springer.com/article/10.1007%2Fs10898-012-9951-y]

（1）基于遗传、进化算法

https://www.ijcai.org/Proceedings/89-1/Papers/122.pdf

https://blog.coast.ai/lets-evolve-a-neural-network-with-a-genetic-algorithm-code-included-8809bece164

（2）粒子群优化（Particle Swarm Optimization, PSO）

https://visualstudiomagazine.com/articles/2013/12/01/neural-network-training-using-particle-swarm-optimization.aspx

https://ieeexplore.ieee.org/document/1202255/?reload=true

任务学习44: 过拟合

• 过拟合 （Overfitting)

网络在训练数据集上的准确率很⾼，但是在测试集上的准确率⽐较低

• 过拟合的解决⽅ٛ案

（1）DropOut

（2）$L_2$正则化

（3）$L_1$正则化

（4）MaxNorm

任务学习45: DropOut 训练

假设⽹络过拟合

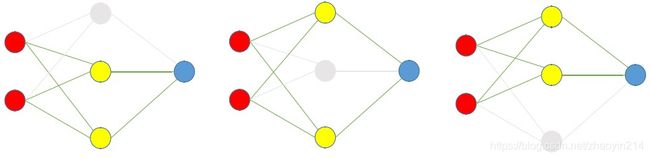
• DropOut

• DropOut训练

给定DropOut rate $r$为$1/3$，则在训练过程中，随机丢弃$1/3$神经元结点，对剩余神经元结点权值进行梯度更新。

• Dropout使用

所有神经元结点均参与推理，但各神经元结点权值需要乘以$1-r$（1 - DropOut rate）

任务学习46: 正则化

• $L_2$正则化

损失函数（loss function）$f(\theta )$中的每一个权值${\theta }_i$，都对损失函数加上$\frac{1}{2}\lambda {\theta }_i^2$。其中，$\lambda >0$是正则化的强度。

训练过程中，每一次权值更新的时候都额外加上这一步：

$${\theta }_i={\theta }_i-\lambda {\theta }_i$$

正则化的目的是使权值的绝对值减小，权值的绝对值越大，减小的程度越强；

$L_2$正则化使得大多数权值的值都不为零，但是绝对值都比较小。

• $L_1$正则化

损失函数$f(\theta )$中的每一个权值${\theta }_i$，都对损失函数加上$\lambda \left|{\theta }_i\right|$。其中$\lambda >0$正则化的强度。

训练过程中，每一次权值更新的时候都额外加上这一步：

$${\theta }_i=\{\begin{array}{ll}{\theta }_i-\lambda ,& {\theta }_i>0\\ {\theta }_i+\lambda ,& {\theta }_i\le 0\end{array}$$

$L_1$正则化的目的是使得许多权值的绝对值接近$0$，其它那些权值不接近于$0$的权值对应的特征就是对输出有影响的特征。因此$L_1$正则化可以用于特征选择。

任务学习47: 最大范数约束 神经元的初始化

• 最⼤֒范数约束（Max Norm）

为每一个神经元对应的权值向量设置一个最大第二范数值$c$，这个值通常设为$3$。如果一个神经元的第二范数值大于$c$，则将每个系数值按比例缩小，使得第二范式值等于$c$。

训练过程中，每一次权值更新的时候都额外加上这一步：

$${\theta }_i=\{\begin{array}{ll}{\theta }_i\ast \frac{c}{\Vert \theta \Vert },& \Vert \theta \Vert >c\\ {\theta }_i,& \Vert \theta \Vert \le c\end{array}$$

最大范数约束可以防止由于训练步长较大引发的过拟合。

• 神经元系数的初始化

偏置系数（bias）：初始化为$O$

权值系数：初始化为

$${\theta }_i=\text{np.random.randn(n) * sqrt(2 / n)}$$，其中，$n$为神经元的输入向量的元素个数。

范数