图神经网络关系抽取论文阅读笔记(二)
1 用于关系抽取的生成式参数图神经网络
论文:Graph Neural Networks with Generated Parameters for Relation Extraction(2019 ACL)
1.1 创新点
-
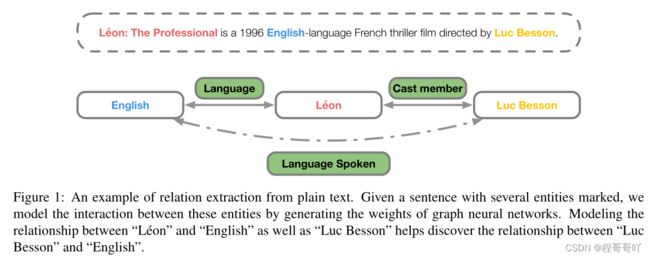
传统的图神经网络在进行NLP任务时,图的拓扑结构都是预先定义好的,之后再用于节点之间消息传递。本文提出一种具有生成参数的新型图神经网络模型,实现了富文本信息的关系消息传递,也就是说图的结构信息(如邻接矩阵、定点值等)可以根据输入的文本信息自动生成,自动构建出GNN的图结构。同时提出的模型还具备处理多条关系推理的能力,可用于处理非结构化输入数据(如自然语言)的关系推理。如图所示:
-
将提出的图神经网络模型用于关系抽取,证明了它在多跳关系推理方面的能力,同时还给出了三个远程监督的数据集,用于后续研究。
1.2 模型架构
给定一个文本序列,其可能包含m个实体,关系抽取的任务是对每一个实体对预测出一个标签。GP-GNN模型是由一个全连接图构成的 G = ( V ( 实 体 集 合 ) , E ( 边 集 合 ) ) \mathcal{G}=(\mathcal{V(实体集合)}, \mathcal{E(边集合)}) G=(V(实体集合),E(边集合));
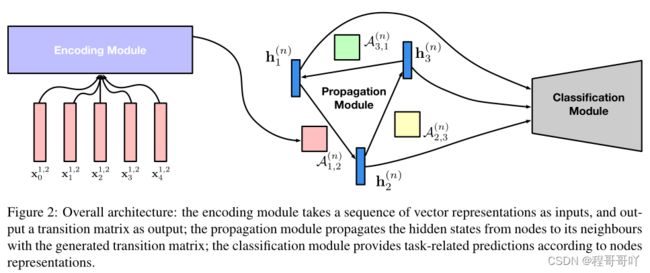
整个GP-GNN模型架构由三部分组成:(1)encoding 模块。(2)传播模块。(3)分类模块进行关系推理。
1.2.1 GP-GNNs用于关系抽取
给定一个句子: s = x 0 i , j , x 1 i , j , … , x l − 1 i , j s=x_0^{i, j}, x_1^{i, j}, \ldots, x_{l-1}^{i, j} s=x0i,j,x1i,j,…,xl−1i,j ,一个关系集合R,和一个实体集合 V s = { v 1 , v 2 , … , v ∣ V s ∣ } \mathcal{V}_s=\left\{v_1, v_2, \ldots, v_{\left|\mathcal{V}_s\right|}\right\} Vs={v1,v2,…,v∣Vs∣},其中 v i v_i vi可能包含一个或者几个单词。
1.2.2 Encoding Module
传统的图神经网络一般会显式的定义边,然而在自然语言中没有这样的显式的边存在,因此就认为这是一个全连接图,也就是说每个单词都会和句子中的其他单词有联系。这些联系就用边的权重矩阵表示,这个权重矩阵不是通过随机初始化再进行反向传播得来的,而是通过句子中单词的向量变换生成而来的。
对于当前输入的文本,得到特征表示:X代表word embedding,p代表单词x距离实体i和j的position embedding。
E ( x t i , j ) = [ x t ; p t i , j ] E\left(x_t^{i, j}\right)=\left[\boldsymbol{x}_t ; \boldsymbol{p}_t^{i, j}\right] E(xti,j)=[xt;pti,j]
Word Representations:Glove
Position Embedding:将序列中的token标记为三种类型,分别是属于第一个实体,属于第二个实体,非实体。
得到特征表示之后,之后将其送到encode当中:
A i , j ( n ) = [ MLP n ( BiLSTM n ( ( E ( x 0 i , j ) , E ( x 1 i , j ) , ⋯ , E ( x l − 1 i , b e ˋ ′ ) ) } \mathcal{A}_{i, j}^{(n)}=\left[\operatorname { M L P } _ { n } \left(\operatorname { B i L S T M } _ { n } \left(\left(E\left(x_0^{i, j}\right), E\left(x_1^{i, j}\right), \cdots, E\left(x_{l-1}^{\left.i, \text { bè }^{\prime}\right)}\right)\right\}\right.\right.\right. Ai,j(n)=[MLPn(BiLSTMn((E(x0i,j),E(x1i,j),⋯,E(xl−1i, beˋ ′))}
其中这里的 A i , j ( n ) \mathcal{A}_{i, j}^{(n)} Ai,j(n)就是图的权重矩阵。
1.2.3 Propagation Module
传播模块逐层学习节点的表示形式,节点的初始嵌入(即第0层的表示)与任务相关,可以是对节点特征进行编码的嵌入,也可以是one-hot编码嵌入。给定层n的表示形式,n +1 层的表示形式通过下面公式计算,其中 N ( v i ) \mathcal{N}\left(v_i\right) N(vi)表示图G中节点v的邻域, σ \sigma σ表示非线性激活函数。
h i ( n + 1 ) = ∑ v j ∈ N ( v i ) σ ( A i , j ( n ) h j ( n ) ) \mathbf{h}_i^{(n+1)}=\sum_{v_j \in \mathcal{N}\left(v_i\right)} \sigma\left(\mathcal{A}_{i, j}^{(n)} \mathbf{h}_j^{(n)}\right) hi(n+1)=vj∈N(vi)∑σ(Ai,j(n)hj(n))
The Initial Embeddings of Nodes:第0层的hvi和hvj被分别的表示为 h v i ( 0 ) = a subject \mathbf{h}_{v_i}^{(0)}=\boldsymbol{a}_{\text {subject }} hvi(0)=asubject 和 h v j ( 0 ) = a o b j e c t \boldsymbol{h}_{v_j}^{(0)}=\boldsymbol{a}_{\mathrm{object}} hvj(0)=aobject,其中 a subject = [ 1 ; 0 ] ⊤ and a object = [ 0 ; 1 ] ⊤ 3 \boldsymbol{a}_{\text {subject }}=[\mathbf{1} ; \mathbf{0}]^{\top} \text { and } \boldsymbol{a}_{\text {object }}=[\mathbf{0} ; \mathbf{1}]^{\top 3} asubject =[1;0]⊤ and aobject =[0;1]⊤3
第一层的构造,对于主体和客体会给一个标记,以便最后进行关系抽取时使用。
1.2.4 Classification Module
在输出模块中,将目标实体(vi,vj)作为输入,然后进行转变:
r v i , v j = [ [ h v i ( 1 ) ⊙ h v j ( 1 ) ] ⊤ ; [ h v i ( 2 ) ⊙ h v j ( 2 ) ] ⊤ ; … ; [ h v i ( K ) ⊙ h v j ( K ) ] ⊤ ] \boldsymbol{r}_{v_i, v_j}=\left[\left[\boldsymbol{h}_{v_i}^{(1)} \odot \boldsymbol{h}_{v_j}^{(1)}\right]^{\top} ;\left[\boldsymbol{h}_{v_i}^{(2)} \odot \boldsymbol{h}_{v_j}^{(2)}\right]^{\top} ; \ldots ;\left[\boldsymbol{h}_{v_i}^{(K)} \odot \boldsymbol{h}_{v_j}^{(K)}\right]^{\top}\right] rvi,vj=[[hvi(1)⊙hvj(1)]⊤;[hvi(2)⊙hvj(2)]⊤;…;[hvi(K)⊙hvj(K)]⊤]
再进行关系预测:
P ( r v i , v j ∣ h , t , s ) = softmax ( MLP ( r v i , v j ) ) \mathbb{P}\left(r_{v_i, v_j} \mid h, t, s\right)=\operatorname{softmax}\left(\operatorname{MLP}\left(\boldsymbol{r}_{v_i, v_j}\right)\right) P(rvi,vj∣h,t,s)=softmax(MLP(rvi,vj))
Loss:
L = ∑ s ∈ S ∑ i ≠ j log P ( r v i , v j ∣ i , j , s ) \mathcal{L}=\sum_{s \in S} \sum_{i \neq j} \log \mathbb{P}\left(r_{v_i, v_j} \mid i, j, s\right) L=s∈S∑i=j∑logP(rvi,vj∣i,j,s)
在实践中,将每个目标实体对堆叠在一起去推断各个实体对之间的潜在关系。
1.3 实验部分
1.3.1数据集
- Distantly labeled set :Sorokin和Gurevych用Wikipedia语料库提出了一个数据集,本文任务与其任务之间有一个小区别:本文任务是提取句子中每对实体之间的关系,而他们的任务是提取给定实体对与上下文实体对之间的关系。 因此需要修改其数据集:1)如果给定三元组中缺少反向边??,例如如果句子中存在三元组(Earth, partof, SolarSystem),则向其添加一个反向标签(Solar System, partof, Earth)如何添加;2)对于所有没有关系的实体对,在它们之间添加了“NA”标签,对所有实验都使用相同的训练集。
- Human annotated test set : 根据Sorokin and Gurevych提供的测试集,需要5个annotator标记数据集,被用来决定是否对每一对实体都使用远程监督,只有所有5个annotator都接受的实例才合并到人工标注的测试集中,最终测试集中有350个句子和1,230个三元组。
- Dense distantly labeled test set : 进一步从远距离标记的测试集中拆分出一个密集的测试集,标准是:实体数量应严格大于2;句子的真实标签中必须至少有一个圆(至少有三个实体)(圆的每个边都有一个非“NA”标签)。该测试集可用于测试论文方法在实体之间具有复杂相互作用的句子上的表现,该测试集中有1,350个句子、超过17,915个三元组和7,906个关系。
1.3.2 实验效果
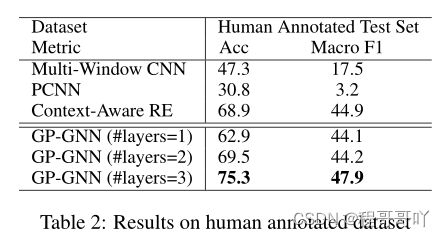
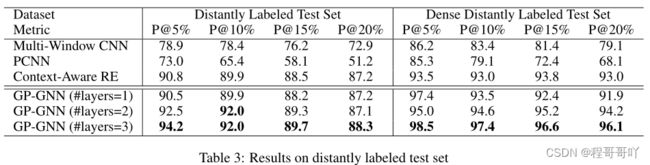
从表2和表3中可以看出,本文最佳模型在所有三个测试集上的性能均明显优于所有基模型。这些结果表明GP-GNN模型可以使用自然语言生成的参数对完全连接的图成功进行推理。这些结果还表明本模型不仅在句子级关系提取上表现良好,而且在袋级关系提取上也有所改进。
层数表示模型的推理能力,K层模型具有推断K跳关系的能力。为了证明层数的影响,比较了具有不同层数的模型。从表2和表3中可以看到,在所有三个数据集上,三层模型均达到最佳。
1.4 论文总结
解决了利用GNN与自然语言进行关系推理的问题,提出的模型GP-GNNs通过将自然语言编码为参数并执行层与层之间的传播来解决关系消息传递任务。 新模型也可以被认为是解决非文本输入(例如文本,图像,视频,音频)的图生成问题的通用框架,可以实现多模态。在这项工作中,证明了其在预测自然语言和袋级实体之间的关系方面的有效性,并表明通过在推理中考虑更多跃点,关系提取的效果可以得到显着改善。
1.5 个人点评
参数自动生成的图神经网络(GP-GNN)是本文的主要亮点,既实现了端到端关系抽取也实现了多模态;但是GP-GNN的原理实在没整明白,感觉论文中很多细节也没有说明白,导致看完了对原理还是一脸懵逼,比如图权重矩阵的生成就很匪夷所思,词向量和位置向量拼到一起丢进Bilstm和MLP就出来了, A i , j ( n ) = [ MLP n ( BiLSTM n ( ( E ( x 0 i , j ) , E ( x 1 i , j ) , ⋯ , E ( x l − 1 i , b e ˋ ′ ) ) } \mathcal{A}_{i, j}^{(n)}=\left[\operatorname { M L P } _ { n } \left(\operatorname { B i L S T M } _ { n } \left(\left(E\left(x_0^{i, j}\right), E\left(x_1^{i, j}\right), \cdots, E\left(x_{l-1}^{\left.i, \text { bè }^{\prime}\right)}\right)\right\}\right.\right.\right. Ai,j(n)=[MLPn(BiLSTMn((E(x0i,j),E(x1i,j),⋯,E(xl−1i, beˋ ′))},这是实在不好理解,为什么权重矩阵可以这么搞就获得了呢?
而且这个实体顶点的初始值设置也很奇怪为什么是 a subject = [ 1 ; 0 ] ⊤ and a object = [ 0 ; 1 ] ⊤ 3 \boldsymbol{a}_{\text {subject }}=[\mathbf{1} ; \mathbf{0}]^{\top} \text { and } \boldsymbol{a}_{\text {object }}=[\mathbf{0} ; \mathbf{1}]^{\top 3} asubject =[1;0]⊤ and aobject =[0;1]⊤3,也没想明白。
最后实验是在自己的三个远程监督数据集上做的,也没整明白,为什么不在其他有监督的数据集上做,单纯是为了验证关系推理能力吗?