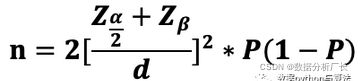数据分析--ABtest
目录
1、ABtest优势:
2、正交实验VS互斥实验?
3、流程:
4、多个试验同时发生时如何分层?
5、Hash分流
6、辛普森悖论
7、最小样本量计算
1、ABtest优势:
解决主观意见的分歧;
快速试错,确定收益预期;
刻画因果;
建立数据驱动的闭环;
降低风险,为迭代提供保障。
2、正交实验VS互斥实验?
正交实验:每个独立试验为一层,为保证各层之间互不影响,一份流量穿越每层试验时,会再次随即打散,且随机效果离散,这一过程叫做正交,这样的试验叫做正交试验。
正交实验能够最大化的保证各层试验互相独立,确保各个试验不会相互影响。
互斥实验:即为在同一层中拆分流量,且不论如何拆分,不同的流量是不重叠的。
互斥试验是在流量足够的情况下进行的分流策略,各个试验之间也不会相互影响。
3、流程:
1)一个客户进入到我们的APP时,会在客群的部分做一次筛选,即试验是否是有划分客群,如果有客群划分,则需要判断新来的客户是否命中我们的试验客群;
2)第二步我们要判断需要进行什么类型的试验,正交还是互斥?以及此次试验需要切分多少流量,5%还是10%?
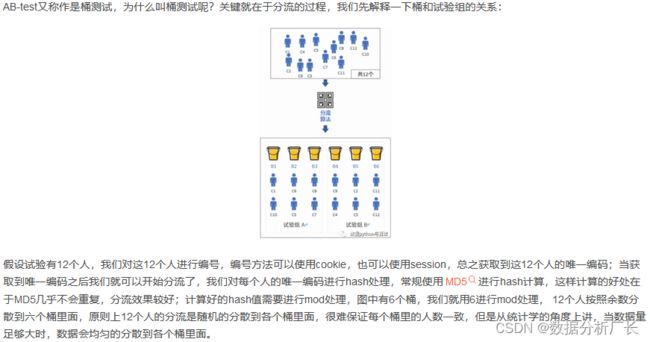
3)经过了客群识别和流量切分后,我们的客户来到了试验分组部分,系统采集客户访问的cookie/session信息计算出唯一hash值,并对这一hash值做mod处理;
4)mod处理之后的数据会被分到t个桶中的某一个,然后再根据一定的比例和算法将t个桶中的数据分成三组,即:A组、A组和B组,假设分流比例为:1/3,1/3,1/3;
5)A-A组即为旧版本对照组,用来检验分流是否有效,如果A-A组不显著,说明数据不受系统性因子影响,分流是有效的;A-B组即为新旧版本的对照组,其中B组为新版本;
6)A-A-B组的数据比较即为试验数据分析,分析人员借此完成试验的效果检验,确定试验是否显著;
4、多个试验同时发生时如何分层?
正交、互斥两种试验是为了能够充分高效的使用流量,实验中往往是多组实验同时存在,既有正交,又有互斥。
域1和域2互斥拆分流量,域2中的流量穿过1-1、1-2、1-3,进入2和3层,1-1、1-2、1-3是互斥的,1、2、3是正交的,上层的流量大于等于下层。
1、2、3层可能为ui层、搜索结果层、广告结果层,这几个层级没有任何关联,如果不同层之间进行试验相互关联,就需要进行互斥实验,互斥试验要尽可能保证只有一个变量。
5、Hash分流
桶分流完成后,将这些桶哦ing军分成两组,原则是保证随机性和平均分配。
6、辛普森悖论
概念:在不同组别中结论相同,但是总体评价时却相反。(量变不等于质变)
原因:在分组时没有考虑隐含特征,分组不均衡,例如上图性别不均衡。
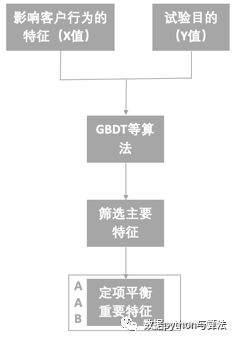
解决:定向试验
在进行试验之前,先做一次实验分析,确定对试验影响较大的因素,然后通过分流的权重设置来均衡各个组之间的特征差异,因素确认用到的方法较多,比如GBDT,随机森林等。
试验时,对分组特征监控,如果某一特征在某一组中偏小,就增加这一特征在这一组的分配权重,以保证特征的一致性。
分层试验、交叉试验、定向实验是我们规避辛普森悖论的有力工具。
7、最小样本量计算
统计计算主要应用在效果评估领域。客户经过分流之后在各个试验组中产生数据,统计的作用即为查看对应组的样本量是否达到最小样本量,数据之间是否存在显著性差异,以及进行差异大小的比较。
最小样本量是按照统计功效进行计算的,主要分两类:绝对值类(例如:UV)和比率类(例如:点击率)。
均值类:
在试验过程中,大部分场景是进行比率类指标的比较,单纯的计算绝对值是没有价值的,而且对于试验效果来讲,绝对值的比较可以转化为比率的比较,所以在计算过程中,我们统一成比率计算,以方便口径统一和数值比较。
比率类最小样本量计算:
其中Z为z系数,统计中Z值有一个固定的Z值表,可以依据α和β指标确定出对应的Z值,工业应用中一般默认使用α=0.1(单尾)和β=0.2,因此公式中:
Zα/2+Zβ=Z0.05+Z0.2=1.6449+0.84=2.4849
可以定为固定值。
当方差已知的情况下,使用Z检验;未知的时候,使用t检验