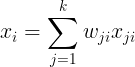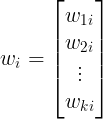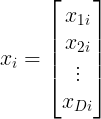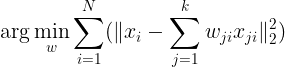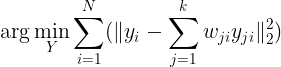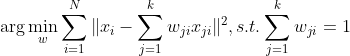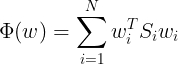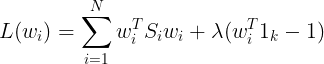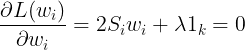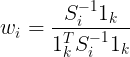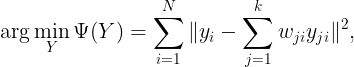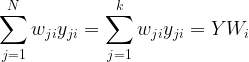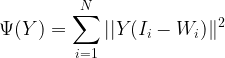LLE原理及推导过程
1.概述
所谓LLE(局部线性嵌入)即”Locally Linear Embedding”的降维算法,在处理所谓流形降维的时候,效果比PCA要好很多。
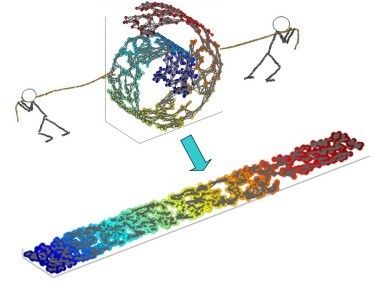
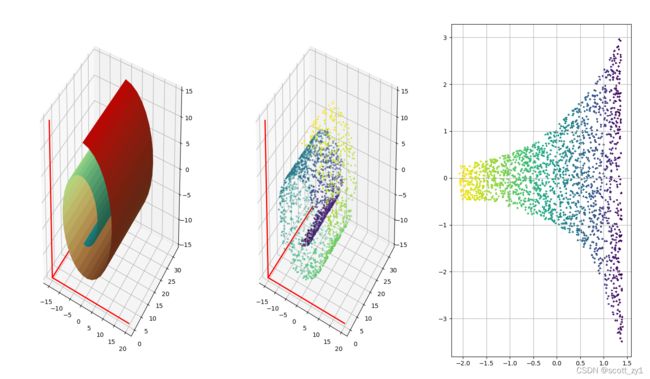
首先,所谓流形,我们脑海里最直观的印象就是Swiss roll,在吃它的时候喜欢把它整个摊开成一张饼再吃,其实这个过程就实现了对瑞士卷的降维操作,即从三维降到了两维。降维前,我们看到相邻的卷层之间看着距离很近,但其实摊开成饼状后才发现其实距离很远,所以如果不进行降维操作,而是直接根据近邻原则去判断相似性其实是不准确的。
LLE的降维实现过程,直观的可视化效果如下图1所示:
2.LLE的原理
所谓局部线性,即认为在整个数据集的某个小范围内,数据是线性的,就比如虽然地球是圆的,但我们还是可以认为我们的篮球场是个平面;而这个“小范围”,最直接的办法就是k-近邻原则。这个“近邻”的判断也可以是不同的依据:比如欧氏距离,测地距离等。
既然是线性,则对每个数据点 ![]() (D维数据,即
(D维数据,即![]() 的列向量),可以用其
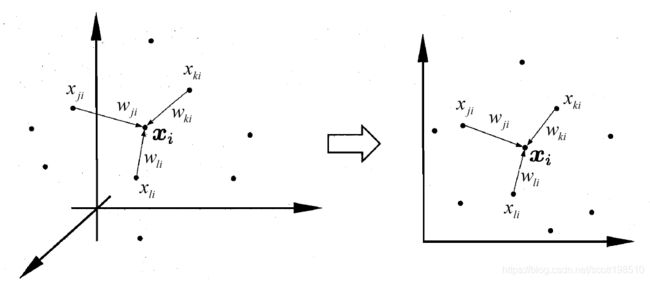
的列向量),可以用其![]() 近邻数据点的线性组合来表示(见上图2),即:
近邻数据点的线性组合来表示(见上图2),即:
上式中,![]() 是
是 ![]() 的列向量,
的列向量,![]() 是
是 ![]() 的第
的第 ![]() 行,
行, ![]() 是
是 ![]() 的第
的第 ![]() 个近邻点
个近邻点![]() ,即
,即
特别注意:此处![]() 中的维度为D,切不可把
中的维度为D,切不可把![]() 视为
视为![]() 中的第j个元素,只是这里的表示刚好凑巧相同。
中的第j个元素,只是这里的表示刚好凑巧相同。
通过使下述Loss-function最小化:
求解上式可得到权重系数
![]()
其中 ![]() (维度为kXN)对应于
(维度为kXN)对应于 ![]() 个数据点,即
个数据点,即 ![]() 列
列 ![]() 。
。
接下来是LLE中又一个假设:即认为将原始数据从D维降到d维后,![]() ,其依旧可以表示为其k近邻的线性组合,且组合系数不变,即 仍然是
,其依旧可以表示为其k近邻的线性组合,且组合系数不变,即 仍然是![]() ,再一次通过最小化loss function:
,再一次通过最小化loss function:
最终得到降维后位于低维空间的的数据:
![]()
3.算法推导过程
step 1:确定近邻点
运用k近邻算法得到每个数据 ![]() 的
的 ![]() 近邻点:
近邻点:
![]()
step 2: 求解权重系数矩阵
即求解如下有约束优化问题:
在推导之前,我们首先统一下数据的矩阵表达形式
输入: ![]()
权重: ![]()
则可逐步推导出权重系数矩阵的表达式:
将 ![]() 看做局部协方差矩阵, 即:
看做局部协方差矩阵, 即:
![]()
其中 ![]() 为
为 ![]() 的元素全1的列向量,就上述表达式而言,局部协方差矩阵
的元素全1的列向量,就上述表达式而言,局部协方差矩阵![]() 是个
是个![]() 的矩阵,其分母实质是矩阵
的矩阵,其分母实质是矩阵![]() 逆矩阵的所有元素之和,而其分子是
逆矩阵的所有元素之和,而其分子是![]() 的逆矩阵对行求和后得到的列向量。
的逆矩阵对行求和后得到的列向量。
step 3: 映射到低维空间
即求解下述有约束优化问题:
![]()
输出结果即低维空间向量组成的矩阵![]() :
:
![]()
首先,用一个 ![]() 的稀疏矩阵(sparse matrix)
的稀疏矩阵(sparse matrix) ![]() 来表示
来表示![]() :
:
对 ![]() 的近邻点
的近邻点 ![]() :
: ![]()
否则 : ![]()
因此:
其中,
![]()
其中,![]() 是方阵
是方阵 ![]() 的第
的第![]() 列 ,
列 , ![]() 是单位矩阵
是单位矩阵 ![]() 的第
的第![]() 列,
列,![]() 对应矩阵
对应矩阵![]() 第
第 ![]() 列,所以 :
列,所以 :
由矩阵相关知识可知:对矩阵 ![]() ,有
,有
![]()
由于![]() 对应的是矩阵的一列,好比上述中
对应的是矩阵的一列,好比上述中![]() ,所以对于整个矩阵而言
,所以对于整个矩阵而言![]() 类比上述矩阵
类比上述矩阵![]() ,所以:
,所以:
![]()
![]()
再一次使用拉格朗日乘子法:
![]()
求导:
进一步得到 ![]() ,再由
,再由![]() ,注意此时
,注意此时
![]()
即: ![]()
可见![]() 其实是
其实是![]() 的特征向量构成的矩阵,为了将数据降到
的特征向量构成的矩阵,为了将数据降到 ![]() 维,我们只需取
维,我们只需取![]() 的最小的
的最小的 ![]() 个非零特征值对应的特征向量,而一般第一个最小的特征值接近0,我们将其舍弃,最终按从小到大取前
个非零特征值对应的特征向量,而一般第一个最小的特征值接近0,我们将其舍弃,最终按从小到大取前 ![]() 个特征值对应的特征向量。
个特征值对应的特征向量。
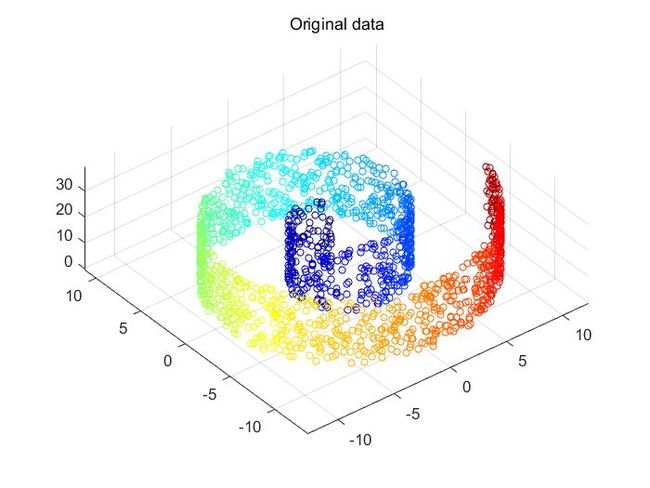
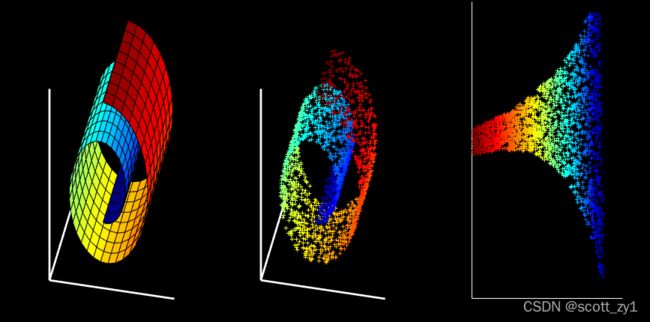
对swiss roll数据集进行了LLE降维。原始的数据如下:
Fig.1. Swill roll数据集。
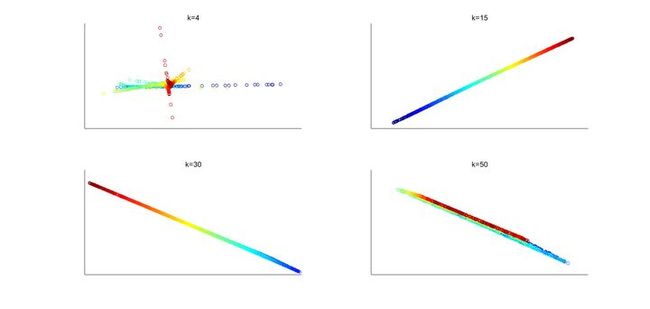
通过LLE降维后的结果如下:
Fig. 2. LLE降维在不同k值的二维分布结果。k代表在k近邻算法时选取的最近邻个数。
可以看出,当k取值较小(k=4)时,算法不能将数据很好地映射到低维空间,因为当近邻个数太少时,不能很好地反映数据的拓扑结构。当k值取值适合,这里选取的是k=15,可见不同颜色的数据能很好地被分开并保持适合的相对距离。但若k取值太大,如k=50,不同颜色的数据开始相互重叠,说明选取的近邻个数太多则不能反映数据的流形信息。
4.其它说明
1. 为什么上述推导最后取最小特征值而不是最大特征值:
![]()
由于最终待优化项是上述表达式,而基于拉格朗日乘子求偏微分得到:
![]()
两者结合,再有约束条件 ![]() , 则:
, 则:
![]()
显而易见, 此时要想使得优化表达式取最小值,则对应的只能是取最小的特征值。
2. LLE与其它流形学习算法比如LE、t-SNE的差异在哪里:
关于不同流形学习算法的差异及比较可参阅 本专栏内以下博客 Laplacian Eigenmaps原理及推导过程 、t-SNE原理与推导 、 机器学习中的流形学习算法
5.代码实现
# lle.py
"""
LLE ALGORITHM (using k nearest neighbors)
X: data as D x N matrix (D = dimensionality, N = #points)
k: number of neighbors
dmax = max embedding dimensionality
Y: lle(X,k,dmax) -> embedding as dmax x N matrix
"""
import numpy as np
from scipy.sparse import csr_matrix,lil_matrix
from scipy.sparse.linalg import eigs
def lle(X, k, d, sparse = True):
D, N = X.shape
print('LLE running on {} points in {} dimensions\n'.format(N,D))
# Step1: compute pairwise distances & find neighbors
print('-->Finding {} nearest neighbours.\n'.format(k))
X2 = np.sum(X**2,axis = 0).reshape(1,-1) # 1xN
distance = np.tile(X2,(N,1)) + np.tile(X2.T, (1, N)) - 2 * np.dot(X.T,X) # NxN
index = np.argsort(distance,axis=0)
neighborhood = index[1:1+k,:] # kxN filter itself
# Step2: solve for reconstruction weights
print('-->Solving for reconstruction weights.\n')
if (k>D):
print(' [note: k>D; regularization will be used]\n')
tol = 1e-3 # regularlizer in case constrained fits are ill conditioned
else:
tol = 0
w = np.zeros((k,N))
for ii in range(N):
xn = X[:,neighborhood[:,ii]] - np.tile(X[:,ii].reshape(-1,1),(1,k)) # shift ith pt to origin
S = np.dot(xn.T, xn) # local covariance,xn = Xi-Ni
S = S + np.eye(k,k) * tol * np.trace(S) # regularlization (k>D)
Sinv = np.linalg.inv(S) # inv(S)
w[:,ii] = np.dot(Sinv,np.ones((k,1))).reshape(-1,) # solve Cw=1
w[:,ii] = w[:,ii]/sum(w[:,ii]) # enforce sum(wi)=1
# Step 3: compute embedding from eigenvectors of cost matrix M = (I-W)'(I-W)
print('-->Computing embedding to get eigenvectors .\n')
if sparse: # parse solution
M = lil_matrix(np.eye(N, N)) # use a sparse matrix lil_matrix((N,N))
for ii in range(N):
wi = w[:,ii].reshape(-1,1) # kx1, i point neighborhood (wji)
jj = neighborhood[:,ii].tolist() # k,
M[ii,jj] = M[ii,jj] - wi.T
M[jj,ii] = M[jj,ii] - wi
M_temp = M[jj,:][:,jj].toarray() + np.dot(wi,wi.T)
for ir, row in enumerate(jj): ### TO DO
for ic, col in enumerate(jj):
M[row,col] = M_temp[ir,ic]
else: # dense solution
M = np.eye(N, N) # use a dense eye matrix
for ii in range(N):
wi = w[:,ii].reshape(-1,1) # kx1
jj = neighborhood[:,ii].tolist() # k,
M[ii,jj] = M[ii,jj] - wi.reshape(-1,)
M[jj,ii] = M[jj,ii] - wi.reshape(-1,)
M_temp = M[jj,:][:,jj] + np.dot(wi,wi.T) # kxk
for ir, row in enumerate(jj): ### TO DO
for ic, col in enumerate(jj):
M[row,col] = M_temp[ir,ic]
M = lil_matrix(M)
# Calculation of embedding
# note: eigenvalue(M) >=0
eigenvals,Y = eigs(M, k = d+1, sigma = 0 ) # Y-> Nx(d+1)
Y = np.real(Y)[:,:d+1] # get d+1 eigenvalue -> eigenvectors
Y = Y[:,1:d+1].T * np.sqrt(N) # bottom evect is [1,1,1,1...] with eval 0
print('Done.\n')
# other possible regularizers for k>D
# S = S + tol*np.diag(np.diag(S)) # regularlization
# S = S + np.eye(k,k)*tol*np.trace(S)*k # regularlization
return Y# test_lle.py
import numpy as np
import math
#import matplotlib
#matplotlib.use('Agg')
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
from lle import lle
# Swill Roll
def plot_swill_roll(N =2000,k=12,d=2,sparse =True):
# Plot true manifold
tt0 = (3*math.pi/2)*(1+2*np.linspace(0,1,51)).reshape(1,-1)
hh = 30 * np.linspace(0,1,9).reshape(1,-1)
xx = np.dot((tt0*np.cos(tt0)).T, np.ones(np.shape(hh)))
yy = np.dot(np.ones(np.shape(tt0)).T,hh)
zz = np.dot((tt0*np.sin(tt0)).T, np.ones(np.shape(hh)))
cc = np.dot(tt0.T, np.ones(np.shape(hh)))
fig = plt.figure(figsize=(18,12))
ax = fig.add_subplot(131, projection='3d')
#ax = Axes3D(fig) # change to 3D figure
cc = cc / cc.max() # normalize 0 to 1
#ax.plot_surface(xx, yy, zz, rstride = 1, cstride = 1, cmap = cm.coolwarm,facecolors=cm.rainbow(cc))
ax.plot_surface(xx, yy, zz, rstride = 1, cstride = 1, facecolors=cm.rainbow(cc))
ax.grid(True)
lnx = -5*np.array([[3,3,3],[3,-4,3]]).T
lny = np.array([[0,0,0],[32,0,0]]).T
lnz = -5*np.array([[3,3,3],[3,3,-3]]).T
ax.plot3D(lnx[0], lny[0], lnz[0],color='red', linewidth = '2', linestyle='-')
ax.plot3D(lnx[1], lny[1], lnz[1],color='red', linewidth = '2', linestyle='-')
ax.plot3D(lnx[2], lny[2], lnz[2],color=[1,0,0], linewidth = '2', linestyle='-')
#plt.axis([-15,20,0,32,-15,15])
ax.set_xlim(-15, 20)
ax.set_ylim(0, 32)
ax.set_zlim(-15, 15)
# Generate sampled data
tt = (3*math.pi/2)*(1+2*np.random.rand(1,N))
tts = tt.reshape(-1,)
height = 21 * np.random.rand(1,N)
X = np.concatenate([tt*np.cos(tt), height, tt*np.sin(tt)],axis=0)
# Scatterplot of sampled data
ax = fig.add_subplot(132, projection='3d')
ax.scatter(X[0,:],X[1,:],X[2,:], marker = '+', s=12, c=tts )
ax.plot3D(lnx[0], lny[0], lnz[0],color='red', linewidth = '2', linestyle='-')
ax.plot3D(lnx[1], lny[1], lnz[1],color='red', linewidth = '2', linestyle='-')
ax.plot3D(lnx[2], lny[2], lnz[2],color=[1,0,0], linewidth = '2', linestyle='-')
#plt.axis([-15,20,0,32,-15,15])
ax.set_xlim(-15, 20)
ax.set_ylim(0, 32)
ax.set_zlim(-15, 15)
# Run LLE algorithm
Y = lle(X,k,d, sparse = sparse)
# Scatterplot of embedding
ax = fig.add_subplot(133)
ax.scatter(Y[0,:],Y[1,:], marker = '+', s=12, c=tts )
ax.grid(True)
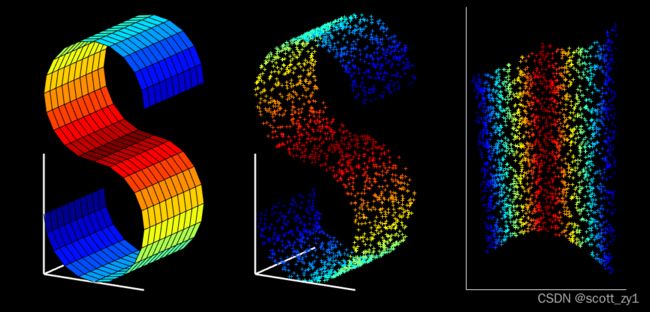
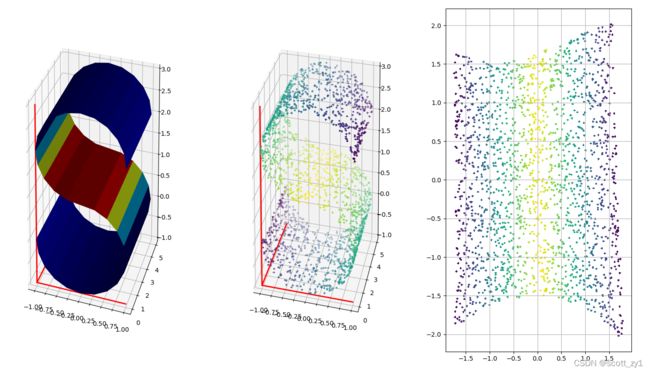
#S-Curve
def plot_s_curve(N =2000,k=12,d=2,sparse = False):
# Plot true manifold
tt = math.pi * np.linspace(-1,0.5,16)
uu = tt[::-1].reshape(1,-1)
tt = tt.reshape(1,-1)
hh = 5 * np.linspace(0,1,11).reshape(1,-1)
xx = np.dot(np.concatenate([np.cos(tt), -np.cos(uu)],axis=1).T, np.ones(np.shape(hh)))
yy = np.dot(np.ones(np.shape(np.concatenate([tt, uu],axis=1))).T, hh)
zz = np.dot(np.concatenate([np.sin(tt), 2 - np.sin(uu)],axis=1).T, np.ones(np.shape(hh)))
cc = np.dot(np.concatenate([tt, uu],axis=1).T , np.ones(np.shape(hh)))
fig = plt.figure(figsize=(18,12))
ax = fig.add_subplot(131, projection='3d')
#ax = Axes3D(fig) # change to 3D figure
#cc = cc / cc.max() # normalize 0 to 1
#ax.plot_surface(xx, yy, zz, rstride = 1, cstride = 1, cmap = cm.coolwarm)
ax.plot_surface(xx, yy, zz, rstride = 1, cstride = 1, facecolors=cm.jet(cc))
ax.grid(True)
lnx = -1*np.array([[1,1,1],[1,-1,1]]).T
lny = np.array([[0,0,0],[5,0,0]]).T
lnz = -1*np.array([[1,1,1],[1,1,-3]]).T
ax.plot3D(lnx[0], lny[0], lnz[0],color='red', linewidth = '2', linestyle='-')
ax.plot3D(lnx[1], lny[1], lnz[1],color='red', linewidth = '2', linestyle='-')
ax.plot3D(lnx[2], lny[2], lnz[2],color=[1,0,0], linewidth = '2', linestyle='-')
#plt.axis([-1,1,0,5,-1,3])
ax.set_xlim(-1, 1)
ax.set_ylim(0, 5)
ax.set_zlim(-1, 3)
# Generate sampled data
angle = math.pi*(1.5*np.random.rand(1,int(N/2))-1)
angle2 = np.concatenate([angle,angle],axis=1).reshape(-1,)
angle2 = angle2/angle2.max()
height = 5 * np.random.rand(1,N)
X = np.concatenate([np.concatenate([np.cos(angle), -np.cos(angle)],axis=1),
height, np.concatenate([np.sin(angle), 2-np.sin(angle)],axis=1)])
# Scatterplot of sampled data
ax = fig.add_subplot(132,projection='3d')
ax.scatter(X[0,:],X[1,:],X[2,:], marker='+', s=12, c = angle2 ) #
ax.plot3D(lnx[0], lny[0], lnz[0],color='red', linewidth = '2', linestyle='-')
ax.plot3D(lnx[1], lny[1], lnz[1],color='red', linewidth = '2', linestyle='-')
ax.plot3D(lnx[2], lny[2], lnz[2],color=[1,0,0], linewidth = '2', linestyle='-')
#plt.axis([-1,1,0,5,-1,3])
ax.set_xlim(-1, 1)
ax.set_ylim(0, 5)
ax.set_zlim(-1, 3)
# Run LLE algorithm
Y = lle(X,k,d, sparse = sparse)
# Scatterplot of embedding
ax = fig.add_subplot(133)
ax.scatter(Y[0,:],Y[1,:], marker='+',s=12, c=angle2 )
ax.grid(True)
if __name__ == '__main__':
plot_swill_roll(N =2000,k=12,d=2)
plot_s_curve(N =2000,k=12,d=2)