正态分布，二维正态分布，卡方分布，学生t分布——概率分布学习 python

目录

基本概念

概率密度函数(PDF: Probability Density Function)

累积分布函数(CDF: Cumulative Distribution Function)

核密度估计（(kernel density estimation）

1.正态分布

概率密度函数（pdf）

正态分布累积分布函数(CDF）

正态分布核密度估计（kde）

正态分布四则运算

二维正态分布（逐渐补充）

马氏距离

2.卡方分布

概率密度函数（pdf）：

 卡方分布表：

卡方分布相关计算

生成卡方分布随机数

3.学生t分布

概率密度函数（pdf）：

---

基本概念

概率密度函数(PDF: Probability Density Function)

连续随机变量的概率分布特性。

累积分布函数(CDF: Cumulative Distribution Function)

在x点左侧事件发生的总和。

CDF特性：

①因为累计分布函数是计算x点左侧的点的数量，所以累计分布函数CDF是单调递增的。

②所有的CDF中，在x趋近-∞时，CDF趋近于0，当x趋近+∞时，CDF趋近于1。

③对于给定的数据集，CDF是唯一的

核密度估计（(kernel density estimation）

核密度估计(kernel density estimation，KDE)是在概率论中用来估计未知的密度函数，属于非参数检验方法之一，通过核密度估计图可以比较直观的看出数据样本本身的分布特征。

scipy中的stats.gaussian_kde可以计算高斯核函数的密度函数，而且提供了直接计算区间的累计密度函数，integrate_box_1d（low=-np.Inf, high=x）。

1.正态分布

表示为：，其中期望为μ，方差为。

概率密度函数（pdf）

python画图效果及代码（包含随机数生成）：

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.mlab as mlab
import matplotlib.cm as cm
import math
import scipy.stats as stats
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号

################################                正态分布             ###########################
# 根据均值、标准差,求指定范围的正态分布概率值
def normfun(x, mu, sigma):
    pdf = np.exp(-((x - mu)**2)/(2*sigma**2)) / (sigma * np.sqrt(2*np.pi))
    return pdf
np.random.seed(0)   ##  定义一个随机数种子
result = np.random.normal(loc=10, scale=16, size=1000) # 均值为0.5,方差为1
# 设定 x,y 轴，载入刚才的正态分布函数
x = np.arange(min(result), max(result), 0.1)
y = normfun(x, result.mean(), result.std())
plt.plot(x, y) # 这里画出理论的正态分布概率曲线
plt.hist(result, bins=20, rwidth=0.8, density=True)     ##  柱状图
plt.title('distribution')
plt.xlabel('temperature')
plt.ylabel('probability')
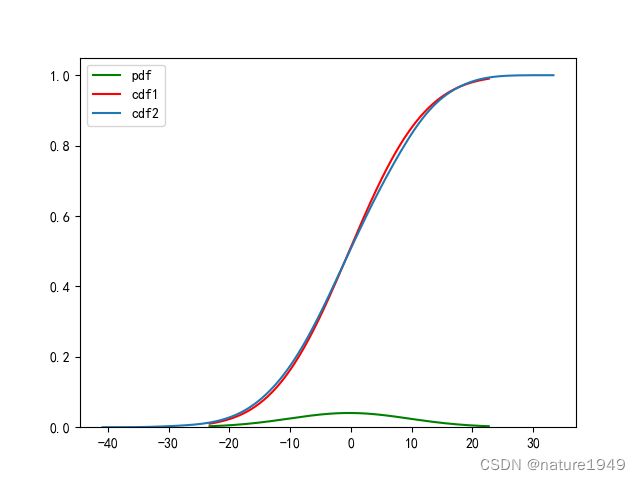
plt.show()

正态分布累积分布函数(CDF）

################################                累积分布函数cdf             ###########################
#计算正态概率密度函数在x处的值
def norm_dist_prob(theta):
    y = stats.norm.pdf(theta, loc=np.mean(data), scale=np.std(data))
    return y

#计算正态分布累积概率值
def norm_dist_cdf(theta):
    y = stats.norm.cdf(theta,loc=np.mean(data), scale=np.std(data))
    return y
##  数据生成
data = np.random.normal(loc=0.0, scale=10, size=1000)

x = np.linspace(stats.norm.ppf(0.01,loc=np.mean(data), scale=np.std(data)),
                stats.norm.ppf(0.99,loc=np.mean(data), scale=np.std(data)), len(data))  #linspace() 函数返回指定间隔内均匀间隔数字的 ndarray。

y1=norm_dist_prob(x)
y2=norm_dist_cdf(x)
plt.plot(x, y1,'g', label='pdf')
plt.plot(x, y2,'r', label='cdf1')
#或
sns.kdeplot(data,cumulative=True, label='cdf2')
plt.legend()

正态分布核密度估计（kde）

################################                核密度估计             ###########################
##  数据生成
data = np.random.normal(loc=0.0, scale=10, size=1000)
##  本程序是根据数据进行概率密度估计
density = stats.gaussian_kde(data)   #, bw_method=None, weights=[i[4] for i in data1]
density.covariance_factor = lambda : .25    #   lambda : .25
density._compute_covariance()
density.set_bandwidth(bw_method='silverman')        ##  调用set_bandwidth 后计算的新带宽用于估计密度的后续评估。可选‘scott’, ‘silverman’
xs = np.linspace(min(data), max(data), 200)
fig, ax = plt.subplots()
ax.plot(xs, density(xs), 'r')
ax.fill_between(xs, density(xs), color="r", alpha=0.1)
ax.hist(data, bins=30, rwidth=0.96, density =True, alpha=0.6,color = 'steelblue', edgecolor = 'w', label = 'dimensional histogram statistic ')

##  或者用seaborn
fig, ax = plt.subplots()
sns.distplot(data, hist=True, kde=True, rug=True, bins=20, ax=ax)
#   通过hist和kde参数调节是否显示直方图及核密度估计(默认hist,kde均为True)
#   bins：int或list，控制直方图的划分
#   rug：控制是否生成观测数值的小细条
#   ax = sns.distplot(x, rug=True, rug_kws={"color": "g"},
#        ...                   kde_kws={"color": "k", "lw": 3, "label": "KDE"},
#        ...                   hist_kws={"histtype": "step", "linewidth": 3,
#        ...                             "alpha": 1, "color": "g"})fig, ax = plt.subplots()

正态分布四则运算

 两个相互独立的正态分布分别满足

则：

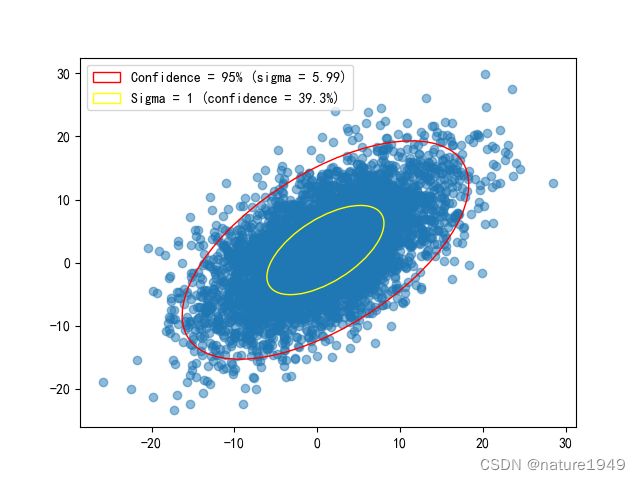
二维正态分布（逐渐补充）

其生成及协方差椭圆的python实现如下：

################################                二维正态分布             ###########################
from matplotlib.patches import Ellipse
def get_error_ellipse_parameters(cov, confidence=None, sigma=None):
    """Returns parameters of an ellipse which contains a specified
    amount of normally-distributed 2D data, where the data is
    characterised by its covariance matrix.
    
    Parameters
    ----------
    cov : array_like
        Input covariance matrix of shape (2,2)
    confidence : float
        Fraction of data points within ellipse. 0 < confidence < 1.
        If confidence is not given, it is calculated according to sigma.
    sigma : float
        Length of axes of the ellipse in standard deviations. If 
        confidence is also given, sigma is ignored.
    
    Returns
    -------
    semi_major : float
        Length of major semiaxis of ellipse.
    semi_minor : float
        Length of minor semiaxis of ellipse.
    angle : float
        Rotation angle of ellipse in radian.
    confidence : float
        Fraction of data expected to lie within the ellipse.
    sigma : float
        Length of major and minor semiaxes in standard deviations.
    """
    cov = np.array(cov)
    if(cov.shape != (2,2)):
        raise ValueError("The covariance matrix needs to be of shape (2,2)")
    if(confidence == None and sigma == None):
        raise RuntimeError("One of confidence and sigma is needed as input argument")
    if(confidence and sigma):
        print("Argument sigma is ignored as confidence is also provided!")
    
    if(confidence == None):
        if(sigma < 0):
            raise ValueError("Sigma needs to be positive")
        #scaling = np.square(sigma)
        scaling = sigma
        confidence = stats.chi2.cdf(scaling, 2)
    if(sigma == None):
        if(confidence > 1 or confidence < 0):
            raise ValueError("Ensure that confidence lies between 0 and 1")
        scaling = stats.chi2.ppf(confidence, 2)
        #sigma = np.sqrt(scaling)
        sigma = scaling
    eigenvalues, eigenvectors = np.linalg.eig(cov)
    maxindex = np.argmax(eigenvalues)
    vx, vy = eigenvectors[:, maxindex]
    angle = np.arctan2(vy, vx)
    semi_minor, semi_major = np.sqrt(np.sort(eigenvalues) * scaling)
    print("With sigma = {:.3f}, {:.1f}% of data points lie within ellipse.".format(sigma, confidence * 100))
    return semi_major, semi_minor, angle, confidence, sigma

mu = [1,2]
cov = [[50,30],[30,50]] #sigma
#   随机数生成
z = stats.multivariate_normal(mu, cov)
data_points = z.rvs(size = 5000)

fig, ax = plt.subplots()
plt.scatter(data_points[:,0], data_points[:,1], alpha = .5)

#   画置信度椭圆
confidence = 0.95
semi_major, semi_minor, angle, confidence, sigma = get_error_ellipse_parameters(cov, confidence = confidence)
ax.add_patch(Ellipse(mu, 2*semi_major, 2*semi_minor, 180*angle/np.pi, facecolor = 'none', edgecolor = 'red', label = 'Confidence = {:.0f}% (sigma = {:.2f})'.format(confidence * 100, sigma)))
sigma = 1
semi_major, semi_minor, angle, confidence, sigma, = get_error_ellipse_parameters(cov, sigma = sigma)
ax.add_patch(Ellipse(mu, 2*semi_major, 2*semi_minor, 180*angle/np.pi, facecolor = 'none', edgecolor = 'yellow', label = 'Sigma = {:.0f} (confidence = {:.1f}%)'.format(sigma, confidence * 100)))
plt.legend()
plt.show()

马氏距离

计算马氏距离（Mahalanobis Distance）。一维马氏距离定义为：

iv = [[1, 0.5, 0.5], [0.5, 1, 0.5], [0.5, 0.5, 1]]
md = distance.mahalanobis([1, 0, 0], [0, 1, 0], iv)
print(md)
#   或
p = np.array([1,1])
distr = np.array([2,2])
cov = [[1,0.2],
        [0.2,1]]
dis = distance.mahalanobis(p, distr, cov)
# p: 一个点    
# distr : 一个分布    
# 计算分布的协方差矩阵    
#cov = np.cov(distr, rowvar=False)    
# 选取分布中各维度均值所在点    
#avg_distri = np.average(distr, axis=0)    
print(dis)

2.卡方分布

卡方分布，也写作：分布。服从自由度为n的卡方分布，记作，其均值为 n，方差为2n。

若n个相互独立的随机变量ξ₁，ξ₂，...,ξn ，均服从标准正态分布N(0,1），则这n个服从标准正态分布的随机变量的平方和构成一新的随机变量，其分布规律称为卡方分布（chi-square distribution）。

 直观说：如果 X1，X2，X3...X„是 n个具有标准正态分布的独立变量,那么其平方和，满足具有n个自由度的分布。

概率密度函数（pdf）：

其中，是Gamma函数，n为自由度，一般情况：

################################                卡方分布             ###########################
for PDF in range(1,8):
    plt.plot(np.linspace(0,15,100),stats.chi2.pdf(np.linspace(0,15,100),df=PDF),label='k='+str(PDF))
plt.tick_params(axis="both",which="major",labelsize=18)
plt.axhline(y=0,color="black",linewidth=1.3,alpha=.7)
plt.legend()

 卡方分布表：

卡方分布相关计算

##  卡方分布相关计算
#   累积分布函数
x = stats.chi2.cdf(5.991, df=2)
#   百分比点函数（与cdf—百分位数相反）
a = stats.chi2.ppf(0.95, df=2)  
print(x,a)

生成卡方分布随机数

#生成随机数
r = stats.chi2.rvs(df=df, size=1000)

3.学生t分布

Student's t-distribution，简称为t分布。

假设随机变量Z服从标准正态分布N(0,1)，另一随机变量V服从m自由度的分布，进一步假设Z和 V 彼此独立，则下列的数量t服从自由度为m的学生t分布:

概率密度函数（pdf）：

################################                t分布             ###########################
x = np.linspace( -3, 3, 100)
plt.plot(x, stats.t.pdf(x,1), label='df=1')
plt.plot(x, stats.t.pdf(x,2), label='df=20')
plt.plot(x, stats.t.pdf(x,100), label = 'df=100')
plt.plot( x[::5], stats.norm.pdf(x[::5]),'kx',  label='normal')
##  累积分布函数cdf
y = stats.t.cdf(x,df=100, loc=0, scale=1)
plt.plot(x,y, label='cdf')
plt.legend()