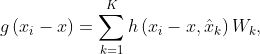什么样的点可以称为三维点云的关键点?
作者 | 秦岭北麓小丹童 编辑 | 3D视觉开发者社区
前言
这个工作来自于香港科技大学和香港城市大学。我们知道,随着三维传感器以及相关扫描技术的进步,三维点云已经成为三维视觉领域内一项十分重要的数据形式。并且随着深度学习技术的发展,许多经典的点云深度学习处理方法被提出来。但是,现有的大多数方法都关注于点云的特征描述子学习。并且,在稠密的点云数据帧中,如果对所有点云都进行处理,将会带来巨大的计算和内存压力。针对这种问题,提取部分具有代表性的关键点则成为一种自然而且有效的策略。但是,什么样的点可以称为三维点云中的关键点呢?这个问题仍然是一个开放的、没有明确答案的问题。
本工作受D2-Net启发,提出了一种新的三维点云关键点定义方式,将其与三维点的特征描述子关联起来,有效的回答了什么是三维点云中的关键点,并验证了该方法检测到的关键点的可重复性。但是,本方法的不足也十分明显。正是由于它将关键点的检测定义在三维点云点特征上,因此,在检测关键点时,需要对输入点云的所有点都提取相应的点特征。这样的话,即使此方法检测到的关键点可以有效用于后续任务,但此方法本身仍需处理完整点云中的所有点,并不能在关键点提取阶段就有效的降低计算和内存压力。
论文相关内容介绍:
论文标题: D3Feat: Joint Learning of Dense Detection and Description of 3D Local Features
作者列表: Xuyang Bai,Zixin Luo, Lei Zhou, Hongbo Fu, Long Quan, Chiew-Lan Tai
摘要:成功的点云配准通常取决于通过有区分性的3D局部特征鲁棒地建立稀疏匹配。尽管基于学习的3D特征描述子发展迅速,但很少有人关注3D特征检测器的学习,更不用说两个任务的联合学习。在本文中,我们将3D全卷积网络用于 3D点云,并提出了一种新颖实用的学习机制,可以稠密预测每个3D点的检测分数和描述特征。特别是,我们提出了一种关键点选择策略,该策略克服了3D点云的固有密度变化,并进一步提出了一种由训练期间的动态特征匹配结果引导的自监督检测器损失。最后,我们的方法在3DMatch和KITTI数据集上进行了评估,在室内和室外场景中都取得了最先进的结果,并在ETH数据集上显示了其强大的泛化能力。在实际使用中,结果表明,通过采用可靠的特征检测器,采样较少数量的特征就足以实现准确和快速的点云对齐。
主要贡献:
1.我们利用基于KPConv的全卷积网络,并采用联合学习框架进行3D局部特征检测和描述,无需构建对偶结构,从而可以进行快速推理。
2. 我们提出了一种新的密度不变关键点选择策略,这是获得3D点云可重复性高的关键点的关键。
3. 我们提出了一种自监督检测器损失,它在训练期间从动态特征匹配结果中获取有意义的引导,从而保证了紧密耦合的描述子和检测器的收敛。
方法介绍:
D2-Net是一种最近提出的一种2D 图像匹配方法,受其启发,我们没有为关键点检测和描述训练单独的网络,而是设计了一个具有双重作用的单个神经网络:稠密特征描述符和关键点检测器。然而,由于点云的不规则性和不同的稀疏性,将D2-Net的思想应用于3D领域并非易事。在下方法,我们将首先描述对不规则 3D点云进行特征描述子提取和和关键点检测的基本步骤,然后解释我们的方法在3D领域中处理稀疏性变化的策略。
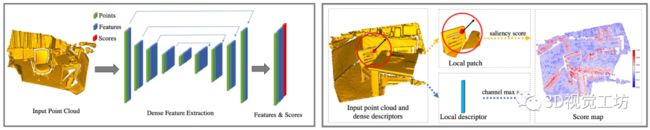
Fig1:(左)D3Feat的网络架构。每个块表示一个使用KPConv代替图像卷积的ResNet块。除了最后一层之外的所有层都使用Batch Normalization和ReLU。(右)关键点检测。在稠密点特征提取之后,我们通过应用显著性分数和通道最大分数来计算关键点检测分数。
一、稠密特征描述子提取
为了解决不规则点的卷积问题并更好地捕获局部几何信息,KPConv方法被提出来,它使用带卷积权重的核点来模拟二维卷积中的核像素,然后在原始点云上定义卷积操作。我们采用KPConv作为我们的骨干网络来执行稠密特征提取操作。下面我们先简单回顾一下KPConv的方法。
以矩阵形式表示给定的一组点![]() 和一组特征
和一组特征![]() ,令
,令![]() 和
和![]() 分别表示中的第i个点及其在
分别表示中的第i个点及其在![]() 中相应的特征。定义在核g上的x点的卷积为
中相应的特征。定义在核g上的x点的卷积为
其中![]() 是x点的半径邻域,
是x点的半径邻域,![]() 是该邻域的支撑点。核函数定义为
是该邻域的支撑点。核函数定义为
其中![]() 是核点
是核点![]() 和支持点之间的相关性函数,
和支持点之间的相关性函数,![]() 是核点
是核点![]() 的权重矩阵,K是核点的个数。我们建议读者参考KPConv原始论文了解更多详细信息。
的权重矩阵,K是核点的个数。我们建议读者参考KPConv原始论文了解更多详细信息。
KPConv的原始公式不是对点云密度不变的,因此,我们在以上公式中添加了一个密度归一化项,它总结了x附近的支持点的数量,以确保卷积是稀疏不变的:
基于归一化核点卷积,我们采用带有跨层连接和残差块的类似UNet的结构来构建全卷积网络,如图1(左)所示。
与仅支持稀疏特征描述子的基于块的方法不同,我们的网络能够在完卷积设置下执行稠密的特征描述子提取。我们网络的输出是二维矩阵![]() 形式的稠密特征图,其中c是特征向量的维度。点的描述子记为
形式的稠密特征图,其中c是特征向量的维度。点的描述子记为![]() :
:
![]()
其中![]() 表示二维矩阵的第i行,特征描述子被L2归一化到单位长度。
表示二维矩阵的第i行,特征描述子被L2归一化到单位长度。
二、稠密关键点检测
D2-Net在特征图的空间和通道维度上的局部最大值,并使用softmax来评估像素的局部最大值以检测二维图像关键点。由于图像的规则结构,他们的方法只是选择相邻像素作为邻域。为了将他们的方法扩展到 3D,这种策略可能会被半径邻域所取代,以处理点云的非均匀采样设置。但是,半径邻域中的相邻点的数量可能会有很大差异。在这种情况下,如果我们简单地使用softmax来评估空间维度上的局部最大值,那么点较少的局部区域本来就会有更高的分数。为了解决这个问题,我们提出了一个密度不变的显著性分数来评估某个点与其局部邻域相比的显著性。给定稠密特征图![]() ,我们认为3D响应
,我们认为3D响应![]() 的集合:
的集合:
![]()
其中![]() 表示二维矩阵的第 k 列。点为关键点的原则是
表示二维矩阵的第 k 列。点为关键点的原则是
![]()
![]()
其中![]() 是
是![]() 的半径邻域。这表示:
的半径邻域。这表示:
首先选择最显著的通道,然后通过它是否是该特定响应图![]() 上其空间局部邻域的最大值来验证。在训练期间,我们通过应用两个分数来使上述过程可微以使其可训练,如图 1(右)所示。
上其空间局部邻域的最大值来验证。在训练期间,我们通过应用两个分数来使上述过程可微以使其可训练,如图 1(右)所示。
1.密度不变显著性得分:该分数旨在评估一个点与其局部邻域中的其他点相比的显著性。在 D2-Net中,评估局部最大值的分数定义为![]() :
:
然而,这个公式对于稀疏性不是不变的。因为分数是通过总和归一化的,这使得稀疏区域固有的比稠密区域具有更高的分数。因此,我们设计了一个密度不变的显著性分数,如下所示:
在这个公式中,一个点的显著性分数被计算为其特征与其局部邻域的平均特征之间的差异。因此,它测量了中心点相对于局部区域中支持点的相对显著性。此外,使用平均响应代替总和可以防止分数受到邻域中点数的影响。
2.通道最大得分:该分数旨在为每个点挑选最显著的通道:
最后,将两个分数都考虑到最终的关键点检测得分:
![]()
因此,在获得输入点云的关键点得分图后,我们选择得分最高的点作为关键点。
三、联合优化特征描述子提取器和关键点检测器
设计合适的监督信号是联合优化特征描述子提取器和关键点检测器的关键。在本节中,我们将首先描述描述子的度量学习损失,然后从自监督的角度设计检测器损失。
1.特征描述子提取损失函数
为了优化特征描述子提取网络,许多工作尝试使用度量学习策略,如对比损失和三元组损失。我们这里将使用对比损失,因为从我们的实验中可以发现它可以提供更好的收敛性能。至于采样策略,我们采用的是hardest in batch策略,使网络专注于最难的点对。
给定一对部分重叠的点云碎片P和Q,以及一个包括n对对应3D点的集合。假设![]() 是一个对应对,对应的两点的描述子记为
是一个对应对,对应的两点的描述子记为![]() 和
和![]() ,得分记为
,得分记为![]() 和
和![]() ,然后将正样本对之间的距离定义为它们的描述子之间的欧几里得距离,即
,然后将正样本对之间的距离定义为它们的描述子之间的欧几里得距离,即
![]()
负样本对之间的距离被定义为:
![]()
其中R是安全半径,![]() 是位于真实对应安全半径之外的最难负样本。对比损失定义为:
是位于真实对应安全半径之外的最难负样本。对比损失定义为:
![]()
![]()
其中![]() 是正对的边界,
是正对的边界,![]() 是负对的边界。
是负对的边界。
2.关键点检测器损失函数
为了优化关键点检测器网络,我们寻求一种损失公式,鼓励容易匹配的对应点比难以匹配的对应点具有更高的关键点检测分数。D2-Net提出了对三元组边界损失的扩展,以联合优化特征描述子提取和关键点检测器:
其中M是三元组边界。然而,这个损失并没有为分数项提供明确的引导,并且这个原始损失公式并不能保证在我们的方法收敛。
因此,我们设计了一个损失项来明确引导分数的梯度。从自监督的角度来看,我们使用on-the-fly特征匹配结果来评估每个对应点的判别性,这将引导每个关键点的得分的梯度传播。如果对应点在当前描述子提取网络下可以匹配,我们希望其得分更高,反之亦然。具体来说,我们将关键点检测器损失定义为
直观地说,如果![]() ,则表明该对应点可以使用最近邻搜索正确匹配,并且损失项将鼓励对应的两点获得的分数
,则表明该对应点可以使用最近邻搜索正确匹配,并且损失项将鼓励对应的两点获得的分数![]() 和
和![]() 更高。相反,如果
更高。相反,如果![]() ,则对应点的描述子不足以使它们建立对应关系,因此损失将鼓励降低其得分。
,则对应点的描述子不足以使它们建立对应关系,因此损失将鼓励降低其得分。
版权声明:本文为奥比中光3D视觉开发者社区特约作者授权原创发布,未经授权不得转载,本文仅做学术分享,版权归原作者所有,若涉及侵权内容请联系删文。
3D视觉开发者社区是由奥比中光给所有开发者打造的分享与交流平台,旨在将3D视觉技术开放给开发者。平台为开发者提供3D视觉领域免费课程、奥比中光独家资源与专业技术支持。
加入【3D视觉开发者社区】学习行业前沿知识,赋能开发者技能提升!
加入【3D视觉AI开放平台】体验AI算法能力,助力开发者视觉算法落地!