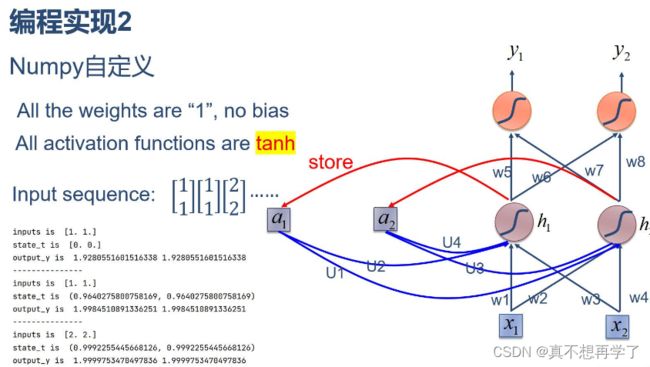
NNDL 作业8:RNN - 简单循环网络
简单循环网络 ( Simple Recurrent Network , SRN) 只有一个隐藏层的神经网络
1. 使用Numpy实现SRN
import numpy as np
inputs = np.array([[1., 1.],
[1., 1.],
[2., 2.]]) # 初始化输入序列
print('inputs is ', inputs)
state_t = np.zeros(2, ) # 初始化存储器
print('state_t is ', state_t)
w1, w2, w3, w4, w5, w6, w7, w8 = 1., 1., 1., 1., 1., 1., 1., 1.
U1, U2, U3, U4 = 1., 1., 1., 1.
print('--------------------------------------')
for input_t in inputs:
print('inputs is ', input_t)
print('state_t is ', state_t)
in_h1 = np.dot([w1, w3], input_t) + np.dot([U2, U4], state_t)
in_h2 = np.dot([w2, w4], input_t) + np.dot([U1, U3], state_t)
state_t = in_h1, in_h2
output_y1 = np.dot([w5, w7], [in_h1, in_h2])
output_y2 = np.dot([w6, w8], [in_h1, in_h2])
print('output_y is ', output_y1, output_y2)
print('---------------')
inputs is [[1. 1.]
[1. 1.]
[2. 2.]]
state_t is [0. 0.]
--------------------------------------
inputs is [1. 1.]
state_t is [0. 0.]
output_y is 4.0 4.0
---------------
inputs is [1. 1.]
state_t is (2.0, 2.0)
output_y is 12.0 12.0
---------------
inputs is [2. 2.]
state_t is (6.0, 6.0)
output_y is 32.0 32.0
---------------
Process finished with exit code 0
2. 在1的基础上,增加激活函数tanh
import numpy as np
inputs = np.array([[1., 1.],
[1., 1.],
[2., 2.]]) # 初始化输入序列
print('inputs is ', inputs)
state_t = np.zeros(2, ) # 初始化存储器
print('state_t is ', state_t)
w1, w2, w3, w4, w5, w6, w7, w8 = 1., 1., 1., 1., 1., 1., 1., 1.
U1, U2, U3, U4 = 1., 1., 1., 1.
print('--------------------------------------')
for input_t in inputs:
print('inputs is ', input_t)
print('state_t is ', state_t)
in_h1 = np.tanh(np.dot([w1, w3], input_t) + np.dot([U2, U4], state_t))
in_h2 = np.tanh(np.dot([w2, w4], input_t) + np.dot([U1, U3], state_t))
state_t = in_h1, in_h2
output_y1 = np.dot([w5, w7], [in_h1, in_h2])
output_y2 = np.dot([w6, w8], [in_h1, in_h2])
print('output_y is ', output_y1, output_y2)
print('---------------')
inputs is [[1. 1.]
[1. 1.]
[2. 2.]]
state_t is [0. 0.]
--------------------------------------
inputs is [1. 1.]
state_t is [0. 0.]
output_y is 1.9280551601516338 1.9280551601516338
---------------
inputs is [1. 1.]
state_t is (0.9640275800758169, 0.9640275800758169)
output_y is 1.9984510891336251 1.9984510891336251
---------------
inputs is [2. 2.]
state_t is (0.9992255445668126, 0.9992255445668126)
output_y is 1.9999753470497836 1.9999753470497836
---------------
Process finished with exit code 0
3. 分别使用nn.RNNCell、nn.RNN实现SRN
class torch.nn.RNNCell(input_size, hidden_size, bias=True, nonlinearity=‘tanh’)[source]
一个 Elan RNN cell,激活函数是tanh或ReLU,用于输入序列。 将一个多层的 Elman RNNCell,激活函数为tanh或者ReLU,用于输入序列。 h ′ = t a n h ( w i h x + b i h + w h h h + b h h ) h'=tanh(w_{ih} x+b_{ih}+w_{hh} h+b_{hh}) h′=tanh(wihx+bih+whhh+bhh) 如果nonlinearity=relu,那么将会使用ReLU来代替tanh。
参数:
input_size – 输入 x x x,特征的维度。
hidden_size – 隐状态特征的维度。
bias – 如果为False,RNN cell中将不会加入bias,默认为True。
nonlinearity – 用于选择非线性激活函数 [tanh|relu]. 默认值为: tanh
输入: input, hidden
input (batch, input_size): 包含输入特征的tensor。
hidden (batch, hidden_size): 保存着初始隐状态值的tensor。
输出: h’
h’ (batch, hidden_size):下一个时刻的隐状态。
变量:
weight_ih – input-hidden 权重, 可学习,形状是(input_size x hidden_size)。
weight_hh – hidden-hidden 权重, 可学习,形状是(hidden_size x hidden_size)
bias_ih – input-hidden 偏置, 可学习,形状是(hidden_size)
bias_hh – hidden-hidden 偏置, 可学习,形状是(hidden_size)
例子:
rnn = nn.RNNCell(10, 20)
input = Variable(torch.randn(6, 3, 10))
hx = Variable(torch.randn(3, 20))
output = []
for i in range(6):
hx = rnn(input[i], hx)
output.append(hx)
来自官网》https://pytorch-cn.readthedocs.io/zh/latest/package_references/torch-nn/#class-torchnnrnncellinput_size-hidden_size-biastrue-nonlinearitytanhsource
import torch
batch_size = 1
seq_len = 3 # 序列长度
input_size = 2 # 输入序列维度
hidden_size = 2 # 隐藏层维度
output_size = 2 # 输出层维度
# RNNCell
cell = torch.nn.RNNCell(input_size=input_size, hidden_size=hidden_size)
# 初始化参数 https://zhuanlan.zhihu.com/p/342012463
for name, param in cell.named_parameters():
if name.startswith("weight"):
torch.nn.init.ones_(param)
else:
torch.nn.init.zeros_(param)
# 线性层
liner = torch.nn.Linear(hidden_size, output_size)
liner.weight.data = torch.Tensor([[1, 1], [1, 1]])
liner.bias.data = torch.Tensor([0.0])
seq = torch.Tensor([[[1, 1]],
[[1, 1]],
[[2, 2]]])
hidden = torch.zeros(batch_size, hidden_size)
output = torch.zeros(batch_size, output_size)
for idx, input in enumerate(seq):
print('=' * 20, idx, '=' * 20)
print('Input :', input)
print('hidden :', hidden)
hidden = cell(input, hidden)
output = liner(hidden)
print('output :', output)
==================== 0 ====================
Input : tensor([[1., 1.]])
hidden : tensor([[0., 0.]])
output : tensor([[1.9281, 1.9281]], grad_fn=)
==================== 1 ====================
Input : tensor([[1., 1.]])
hidden : tensor([[0.9640, 0.9640]], grad_fn=)
output : tensor([[1.9985, 1.9985]], grad_fn=)
==================== 2 ====================
Input : tensor([[2., 2.]])
hidden : tensor([[0.9992, 0.9992]], grad_fn=)
output : tensor([[2.0000, 2.0000]], grad_fn=)
Process finished with exit code 0
import torch
batch_size = 1
seq_len = 3
input_size = 2
hidden_size = 2
num_layers = 1
output_size = 2
cell = torch.nn.RNN(input_size=input_size, hidden_size=hidden_size, num_layers=num_layers)
for name, param in cell.named_parameters(): # 初始化参数
if name.startswith("weight"):
torch.nn.init.ones_(param)
else:
torch.nn.init.zeros_(param)
# 线性层
liner = torch.nn.Linear(hidden_size, output_size)
liner.weight.data = torch.Tensor([[1, 1], [1, 1]])
liner.bias.data = torch.Tensor([0.0])
inputs = torch.Tensor([[[1, 1]],
[[1, 1]],
[[2, 2]]])
hidden = torch.zeros(num_layers, batch_size, hidden_size)
out, hidden = cell(inputs, hidden)
print('Input :', inputs[0])
print('hidden:', 0, 0)
print('Output:', liner(out[0]))
print('--------------------------------------')
print('Input :', inputs[1])
print('hidden:', out[0])
print('Output:', liner(out[1]))
print('--------------------------------------')
print('Input :', inputs[2])
print('hidden:', out[1])
print('Output:', liner(out[2]))
Input : tensor([[1., 1.]])
hidden: 0 0
Output: tensor([[1.9281, 1.9281]], grad_fn=)
--------------------------------------
Input : tensor([[1., 1.]])
hidden: tensor([[0.9640, 0.9640]], grad_fn=)
Output: tensor([[1.9985, 1.9985]], grad_fn=)
--------------------------------------
Input : tensor([[2., 2.]])
hidden: tensor([[0.9992, 0.9992]], grad_fn=)
Output: tensor([[2.0000, 2.0000]], grad_fn=)
Process finished with exit code 0
4. 分析“二进制加法” 源代码(选做)

https://iamtrask.github.io/2015/11/15/anyone-can-code-lstm/
def addBinary(self, a, b):
if len(a) < len(b):
temp = a
a = b
b = temp
a = a[::-1]
b = b[::-1]
extra = 0
new_binary = ""
for index, num in enumerate(a):
if index > len(b) - 1:
b_sum = 0
else:
b_sum = int(b[index])
new_binary = new_binary + str((int(num) + b_sum + extra) % 2)
if int(num) + b_sum + extra > 1: #进位
extra = 1
else:
extra = 0
if extra == 1: #最高位进位
new_binary = new_binary + "1"
return new_binary[::-1]
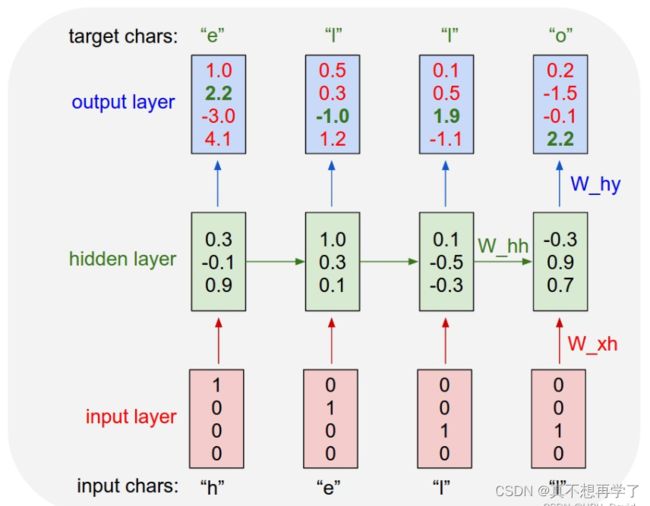
5. 实现“Character-Level Language Models”源代码(必做)
翻译Character-Level Language Models 相关内容
The Unreasonable Effectiveness of Recurrent Neural Networks
论文;
https://arxiv.org/abs/1808.04444
名词缩写
Character-Level Language Models 中译:字符级语言模型
truncated backpropogation throgh time (TBTT) 时间截断的反向传播
Long Short Term Memory( LSTM)长短时记忆网络
部分半机翻:(特别离谱的地方改了一下)
出于多种原因,自然语言文本的字符级建模具有挑战性。
首先,模型必须学习“从头开始”的大量词汇量。
二、天然文本在数百个长距离上表现出依赖关系
或数千个时间步长。
三、字符序列是比单词序列长,因此需要大量更多计算步骤
近年来,强字符级语言模型通常遵循通用模板(Mikolov 等人,2010 年;2011;桑德迈耶,施卢特和内伊2012)。一个复发性 ̈神经网络 (RNN) 通过小批量文本序列进行训练,使用相对较短的序列长度(例如 200令牌)。捕获比批处理序列更长的上下文长度,训练批次按顺序提供,以及前一批中的隐藏状态将转发到当前批次。此过程称为“随时间截断的反向传播”(TBTT),因为梯度计算不会比单个更进一步批次(Werbos 1990)。已经出现了一系列方法公正和改进TBTT(Tallec和Ollivier 2017;柯等人,2017)
虽然这种技术取得了良好的效果,但它增加了训练过程的复杂性,最近的研究表明以这种方式训练的模型实际上并没有使“强”使用长期背景。例如坎德尔瓦尔et al. (2018) 发现基于单词的 LSTM 语言模型仅有效使用大约 200 个上下文tokens(即使提供了更多),并且该词序仅具有效果大约在最后 50 个tokens内
在本文中,我们展示了非循环模型可以在字符级语言建模方面取得优异成绩。具体来说,我们使用transformer的深度网络自我注意层(Vaswani et al. 2017)与因果关系(向后)注意处理固定长度的输入并预测即将到来的角色。模型在来自随机位置的小批量序列训练语料库,没有从一批传递的信息到下一个。
我们的主要发现是transformer架构是非常适合长序列的语言建模和可以替换此域中的 RNN。我们推transformer在这里的成功归功于它能够“快速”在任意距离上传播信息;相比之下,RNN 需要学会逐步向前传递相关信息。
我们还发现,对基本变压器架构的一些修改在这一领域是有益的。最重要的是,我们增加了三个辅助loss,需要模型在中间序列中预测即将到来的字符 (i)位置,(ii)来自中间隐藏表示,以及(iii)在目标位置上,未来多步。这些损失加速收敛,使训练成为可能更深层次的网络。

两层的transformer由4个字符预测第5个字符,因果关系注意掩码将信息限制为从左到右的流动,红色箭头指出的是需要预测的任务。

添加中间位置预测任务到我们的网络。现在,我们预测最终字符 t4 和所有中间字符 T0:3。T3 只能访问 T0:2
因为因果注意面具。所有这些损失在训练期间平等贡献。

在为中间层添加预测任务后的网络。对于此两个图层的示例,完成 25% 的训练后,中间层预测任务的损失将不存在。
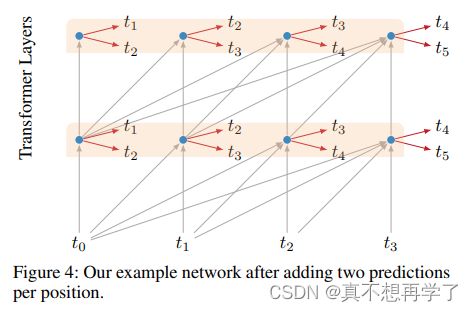
每个位置添加两个预测后的示例网络。
该模型有大约 2.35 亿个参数,大于文本中的字符数8训练语料库。为了规范化模型,我们应用 dropout在注意力层和 ReLU 层中,概率为 0.55。我们使用动量为 0.99 的动量优化器。这训练期间学习率固定为 0.003。我们训练我们的400 万个步骤的模型,每个步骤处理一个批次随机选择的 16 个序列。我们连续降低中间层损耗,如上面的中间层损耗部分所述。从第一层开始,每 62.5K (= 4M× 后12∗64)步骤,我们放弃损失由下一层介绍。按照这个时间表,训练完成一半后,只有最后一层损失存在。
编码实现该模型
import torch.nn as nn
class RNNModel(nn.Module):
def __init__(self, rnn_type, ntoken, ninp, nhid, nlayers, dropout=0.5, tie_weights=False):
super(RNNModel, self).__init__()
self.drop = nn.Dropout(dropout)
self.encoder = nn.Embedding(ntoken, ninp)
if rnn_type in ['LSTM', 'GRU']:
self.rnn = getattr(nn, rnn_type)(ninp, nhid, nlayers, dropout=dropout)
else:
try:
nonlinearity = {'RNN_TANH': 'tanh', 'RNN_RELU': 'relu'}[rnn_type]
except KeyError:
raise ValueError( """An invalid option for `--model` was supplied,
options are ['LSTM', 'GRU', 'RNN_TANH' or 'RNN_RELU']""")
self.rnn = nn.RNN(ninp, nhid, nlayers, nonlinearity=nonlinearity, dropout=dropout)
self.decoder = nn.Linear(nhid, ntoken)
if tie_weights:
if nhid != ninp:
raise ValueError('When using the tied flag, nhid must be equal to emsize')
self.decoder.weight = self.encoder.weight
self.init_weights()
self.rnn_type = rnn_type
self.nhid = nhid
self.nlayers = nlayers
def init_weights(self):
initrange = 0.1
self.encoder.weight.data.uniform_(-initrange, initrange)
self.decoder.bias.data.zero_()
self.decoder.weight.data.uniform_(-initrange, initrange)
def forward(self, input, hidden):
emb = self.drop(self.encoder(input))
output, hidden = self.rnn(emb, hidden)
output = self.drop(output)
decoded = self.decoder(output.view(output.size(0)*output.size(1), output.size(2)))
return decoded.view(output.size(0), output.size(1), decoded.size(1)), hidden
def init_hidden(self, bsz):
weight = next(self.parameters())
if self.rnn_type == 'LSTM':
return (weight.new_zeros(self.nlayers, bsz, self.nhid),
weight.new_zeros(self.nlayers, bsz, self.nhid))
else:
return weight.new_zeros(self.nlayers, bsz, self.nhid)
6. 分析“序列到序列”源代码(选做)
7. “编码器-解码器”的简单实现(必做)
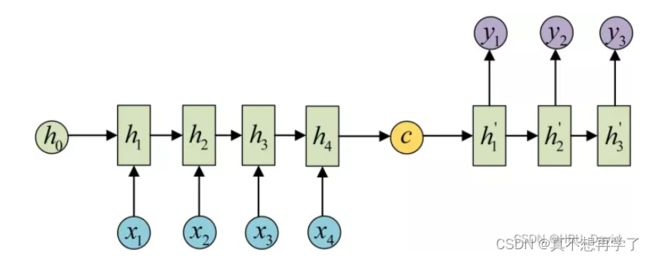
seq2seq的PyTorch实现_哔哩哔哩_bilibili
# -*- coding: utf-8 -*-
import torch
import numpy as np
import torch.nn as nn
import torch.utils.data as Data
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
letter = [c for c in 'SE?abcdefghijklmnopqrstuvwxyz']
letter2idx = {n: i for i, n in enumerate(letter)}
seq_data = [['man', 'women'], ['black', 'white'], ['king', 'queen'], ['girl', 'boy'], ['up', 'down'], ['high', 'low']]
# Seq2Seq Parameter
n_step = max([max(len(i), len(j)) for i, j in seq_data]) # max_len(=5)
n_hidden = 128
n_class = len(letter2idx) # classfication problem
batch_size = 3
def make_data(seq_data):
enc_input_all, dec_input_all, dec_output_all = [], [], []
for seq in seq_data:
for i in range(2):
seq[i] = seq[i] + '?' * (n_step - len(seq[i])) # 'man??', 'women'
enc_input = [letter2idx[n] for n in (seq[0] + 'E')] # ['m', 'a', 'n', '?', '?', 'E']
dec_input = [letter2idx[n] for n in ('S' + seq[1])] # ['S', 'w', 'o', 'm', 'e', 'n']
dec_output = [letter2idx[n] for n in (seq[1] + 'E')] # ['w', 'o', 'm', 'e', 'n', 'E']
enc_input_all.append(np.eye(n_class)[enc_input])
dec_input_all.append(np.eye(n_class)[dec_input])
dec_output_all.append(dec_output) # not one-hot
# make tensor
return torch.Tensor(enc_input_all), torch.Tensor(dec_input_all), torch.LongTensor(dec_output_all)
'''
enc_input_all: [6, n_step+1 (because of 'E'), n_class]
dec_input_all: [6, n_step+1 (because of 'S'), n_class]
dec_output_all: [6, n_step+1 (because of 'E')]
'''
enc_input_all, dec_input_all, dec_output_all = make_data(seq_data)
class TranslateDataSet(Data.Dataset):
def __init__(self, enc_input_all, dec_input_all, dec_output_all):
self.enc_input_all = enc_input_all
self.dec_input_all = dec_input_all
self.dec_output_all = dec_output_all
def __len__(self): # return dataset size
return len(self.enc_input_all)
def __getitem__(self, idx):
return self.enc_input_all[idx], self.dec_input_all[idx], self.dec_output_all[idx]
loader = Data.DataLoader(TranslateDataSet(enc_input_all, dec_input_all, dec_output_all), batch_size, True)
# Model
class Seq2Seq(nn.Module):
def __init__(self):
super(Seq2Seq, self).__init__()
self.encoder = nn.RNN(input_size=n_class, hidden_size=n_hidden, dropout=0.5) # encoder
self.decoder = nn.RNN(input_size=n_class, hidden_size=n_hidden, dropout=0.5) # decoder
self.fc = nn.Linear(n_hidden, n_class)
def forward(self, enc_input, enc_hidden, dec_input):
# enc_input(=input_batch): [batch_size, n_step+1, n_class]
# dec_inpu(=output_batch): [batch_size, n_step+1, n_class]
enc_input = enc_input.transpose(0, 1) # enc_input: [n_step+1, batch_size, n_class]
dec_input = dec_input.transpose(0, 1) # dec_input: [n_step+1, batch_size, n_class]
# h_t : [num_layers(=1) * num_directions(=1), batch_size, n_hidden]
_, h_t = self.encoder(enc_input, enc_hidden)
# outputs : [n_step+1, batch_size, num_directions(=1) * n_hidden(=128)]
outputs, _ = self.decoder(dec_input, h_t)
model = self.fc(outputs) # model : [n_step+1, batch_size, n_class]
return model
model = Seq2Seq().to(device)
criterion = nn.CrossEntropyLoss().to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
for epoch in range(5000):
for enc_input_batch, dec_input_batch, dec_output_batch in loader:
# make hidden shape [num_layers * num_directions, batch_size, n_hidden]
h_0 = torch.zeros(1, batch_size, n_hidden).to(device)
(enc_input_batch, dec_intput_batch, dec_output_batch) = (enc_input_batch.to(device), dec_input_batch.to(device), dec_output_batch.to(device))
# enc_input_batch : [batch_size, n_step+1, n_class]
# dec_intput_batch : [batch_size, n_step+1, n_class]
# dec_output_batch : [batch_size, n_step+1], not one-hot
pred = model(enc_input_batch, h_0, dec_intput_batch)
# pred : [n_step+1, batch_size, n_class]
pred = pred.transpose(0, 1) # [batch_size, n_step+1(=6), n_class]
loss = 0
for i in range(len(dec_output_batch)):
# pred[i] : [n_step+1, n_class]
# dec_output_batch[i] : [n_step+1]
loss += criterion(pred[i], dec_output_batch[i])
if (epoch + 1) % 1000 == 0:
print('Epoch:', '%04d' % (epoch + 1), 'cost =', '{:.6f}'.format(loss))
optimizer.zero_grad()
loss.backward()
optimizer.step()
# Test
def translate(word):
enc_input, dec_input, _ = make_data([[word, '?' * n_step]])
enc_input, dec_input = enc_input.to(device), dec_input.to(device)
# make hidden shape [num_layers * num_directions, batch_size, n_hidden]
hidden = torch.zeros(1, 1, n_hidden).to(device)
output = model(enc_input, hidden, dec_input)
# output : [n_step+1, batch_size, n_class]
predict = output.data.max(2, keepdim=True)[1] # select n_class dimension
decoded = [letter[i] for i in predict]
translated = ''.join(decoded[:decoded.index('E')])
return translated.replace('?', '')
print('test')
print('man ->', translate('man'))
print('mans ->', translate('mans'))
print('king ->', translate('king'))
print('black ->', translate('black'))
print('up ->', translate('up'))
Epoch: 1000 cost = 0.002090
Epoch: 1000 cost = 0.002263
Epoch: 2000 cost = 0.000424
Epoch: 2000 cost = 0.000484
Epoch: 3000 cost = 0.000138
Epoch: 3000 cost = 0.000141
Epoch: 4000 cost = 0.000045
Epoch: 4000 cost = 0.000050
Epoch: 5000 cost = 0.000018
Epoch: 5000 cost = 0.000016
test
man -> women
mans -> women
king -> queen
black -> white
up -> down
Process finished with exit code 0
Seq2Seq的PyTorch实现 - mathor
come from:
https://blog.csdn.net/qq_38975453/article/details/127561213
总结:了解了RNN的原理,并代码实现。同时pytorch的代码也实现了一次。
读英文论文实在令人头疼,有很多代词不认识,全部都机翻吧由不太合适,遇到不认识的单词就查吧,这样看了不到一半就坚持不下去了,还是机翻看的快。。最后大致了解了字符级别的语言模型是怎样的。
这次实验让我认识到,RNN相关的几种应用。RNN主要是要与前面时刻的状态有关联,如果关联太多的话也会是参数量过大的问题的,因此需要dropout一下。
Character-Level Language Models是non_RNN的,他是用transformer来代替网络中的RNN部分并取得更好的效果。他的结构是很巧妙的,有种让人耳目一新的感觉。