《深入浅出图神经网络》读书笔记（1-2基础知识回顾）

基础知识回顾

1.图的概述

1.1 图的相关定义

顶点集合：V，顶点数为N

边集合：E，边数为M

图：$G=(V,E)$

无向边：$(v_i,v_j)$

有向边：$e_{ij}=<v_i,v_j>$

加权图：边上有数字

无权图：各边权重相同

连通图：无孤立节点

非连通图：有孤立节点

二部图：V划分为两个子集A，B，图中的任何一条边$e_{ij}$均符合条件$(v_i\in Aand{v}_j\in B)or(v_i\in Band{v}_j\in A)$

邻居：存在一条边顶点$v_i$连接$v_j$，那么$v_j$是$v_i$的邻居，反之亦然。符号表示邻居集合$N(v_i)$为
$$N(v_i)=\{v_j|\exists e_{ij}\in Eor{e}_{ji}\in E\}$$
度：以$v_i$为端点的边的数目，记为$\text{deg}(v_i)$
$$\begin{gathered} \text{deg}(v_i)=|N(v_i)| \\ \sum _{v_i}\text{deg}(v_i)=2|E| \end{gathered}$$
出度：以$v_i$为起点的边的数目。

入度：以$v_i$为终点的边的数目。

子图：图$G=(V,E),G^{{}^{\prime }}=(V^{{}^{\prime }},E^{{}^{\prime }})$有$V^{{}^{\prime }}\subseteq V,E^{{}^{\prime }}\subseteq E$，称图$G^{{}^{\prime }}$是图$G$的子图。

路径：边序列$P_{ij}=(e_{v_i{P}_1},e_{P_1{P}_2},...,e_{P_m{v}_j})$表示从顶点i到j的一条路径。

路径的长度：$L(P_{ij})=|P_{ij}|$.

顶点的距离：$d(v_i,v_j)=\min (|P_{ij}|)$，两个顶点的距离由它们的最短路径决定。到自身距离为0.

k阶邻居：若$d(v_i,v_j)=k$，$v_j$是$v_i$的k阶邻居。

k阶子图：也叫k-hop。$v_i$的k阶子图是$G_{v_i}^{(k)}=(V,E)$,$V^{{}^{\prime }}=\{v_j|\forall v_j,d(v_i,v_j)\le k\},E^{{}^{\prime }}=e_{ij}|\forall v_j,d(v_i,v_j)\le k$。

1.2 图的存储和遍历

邻接矩阵：
$$A_{ij}=\{\begin{array}{l}1,\text{if}(v_i,v_j)\subseteq E\\ 0,\text{else}\end{array}$$
为节省空间，可以采用稀疏矩阵的格式存储。维度N*N。

关联矩阵：维度N*M。边用编号表示$e_1,...,e_j,...,e_M$
$$B_{ij}=\{\begin{array}{l}1,\text{if}{v}_i与e_j相连\\ 0,\text{else}\end{array}$$

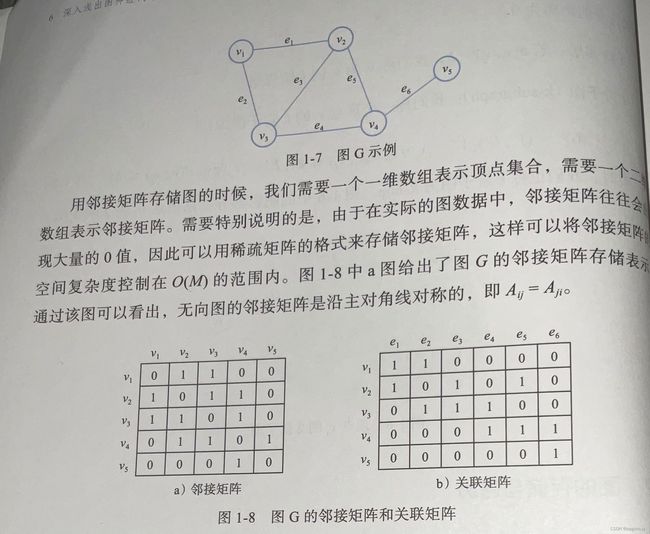
图的遍历：DFS：上述图遍历的顺序12453和BFS：上述图遍历的顺序12345。

1.3 图的应用场景和发展

图也可以叫做网络，顶点和边对应叫做节点和关系。

四类图：

1. 同构图：同构图是指图中的节点类型和关系类型仅有一种，如万维网，这类图数据的信息全部包含在邻接矩阵里。
2. 异构图：节点类型和关系类型多于一种。图数据对象一般多类型，对象之间的交互也多样化，该类图更贴近现实。
3. 属性图：相较于异构图，属性图给图数据增加了额外的属性信息，节点和关系都有标签（节点或关系的类型）和属性（节点或关系的附加描述信息）。
4. 非显式图：非显式图是指数据之间没有显式地定义出关系，需要依据某种规则或计算方式将数据的关系表达出来，进而将数据当做一种图数据研究。如3D视觉中的点云数据，将节点之间的距离转化成关系来研究。

发展过程：

2005年，首次提出图神经网络的概念，在此之前，处理方法都是在数据预处理时将图转换为一组向量，这样会损失大量的结构信息。

2009年，监督学习的方法训练GNN，早期都是以迭代的方式，通过循环神经网络传播邻居信息，直到达到稳定的固定状态来学习节点的表示。这种方法计算量太大。

2012年前后，卷积引入GNN，基于频域卷积操作开发了一种图卷积网络模型，但这种方法在计算时要处理整个图，并需要承担矩阵分解时的很高的时间复杂度，难以扩展到大系统网络。

2016年，简化使得图卷积的操作能够在空域进行，提高了效率。

图数据相关任务的一种分类：

1. 节点层面的任务：分类任务和回归任务。虽然是对节点预测，但也要考虑节点之间的关系。
2. 边层面的任务：分类和预测任务。边的分类是指对边的某种性质进行预测；边的预测是指给定的两个节点之间是否会构成边。
3. 图层面的任务：图层面的任务不依赖于某个节点或某条边的属性，而是从图的整体结构出发，实现分类、表示和生成等任务。一般有对药物分子的分类、酶分类等任务。

2.神经网络基础

2.1 机器学习分类：

按是否有标签分类：

监督学习：训练数据中每个样本都有标签，标签可以指导模型进行学习，学到具有判别性的特种证，从可以对未知样本进行预测。

无监督学习：训练数据中完全没有标签，通过算法从数据中发现一些数据之间的约束关系，比如数据之间的关联、距离关系。典型的算法有聚类。

半监督学习：训练数据之中既有有标签数据，也有无标签数据。

按算法输出分类：

分类问题：输出为离散值；

回归问题：输出为连续值。

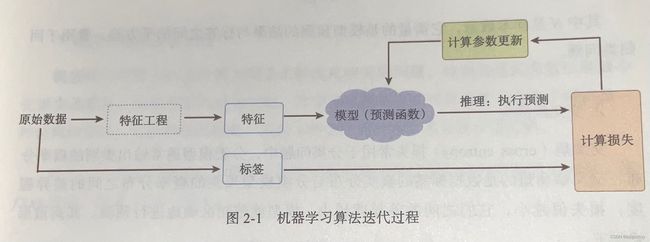
2.2 机器学习流程

1. 提取特征：这些特征可以是人为定义的——特征工程，也可以是算法自动提取——深度学习；
2. 建立模型：传统的机器学习模型有logistic，随机森林等；基于深度学习的方法有多层感知器、卷积神经网络。模型其实就是一个函数，其目的是建立输入到标签之间的映射。
3. 确定损失函数和进行优化求解：选择模型只是确定了一个模型形式，比如使用logistic，它还有一些参数无法确定，因此还无法预测。这个时候就要使用一个数值来量化模型的对错——损失函数，衡量了输出与标签之间的差异程度。

数学模型：模型的输出一般是在每个类别上的概率分布，去概率最大的作为预测结果。
$$y_i^{\ast }=\arg \max (P(Y|x_i))$$
优化求解：整个过程如下
$${\theta }^{\ast }=\arg \min [\frac{1}{N}\sum _{i=1}^{N}L(y_i,f(x_i;\theta ))+\lambda \Phi (\theta )]$$
其实质是调整$f$的参数$\theta$，使得损失函数值达到最小，此时就是最优的模型。其中前面的均值函数是经验风险函数，$L$代表的是损失函数，后面的$\Phi$是正则化项，或者叫惩罚项。

实际优化无法一步优化至最佳，常用迭代法，有如下过程：

如果在训练集取得效果很好，但是在新样本上的效果极差，这种现象称为过拟合；“竭尽全力”无法在训练集上达到很好的效果，称为欠拟合。

2.3 损失函数

平方损失函数：用于预测标签y为实数值的任务中，定义为
$$L(y,f(x;\theta ))=1/2(y-f(x;\theta ){)}^2$$
其不适用于分类问题。

**交叉熵损失函数：**一般用于分类问题。

离散形式如下：
$$L(y,f(x))=H(p,q)=-\frac{1}{N}\sum _{i=1}^{N}p(y_i|x_i)\log [q({\hat{y}}_i|x_i)]$$
其中，$p$代表真实分布，$q$代表预测分布，一般来说样本$x_i$只属于某个类别$c_k$，因此有$p(y_i=c_k|x_i)=1$，在其它类别上概率p均为0。

综上可以写成如下公式
$$L(y,f(x))=-\frac{1}{N}\sum _{i=1}^N\log [q({\hat{y}}_i=|x_i)]$$
可以看出在这种情况下，最小化交叉熵损失的本质就是最大化样本标签的似然概率。

以二分类问题的logistic回归模型为例，若$y_i\in \{0,1\}$，使用logistic回归可以得到样本$x_i$属于类别1的概率为$q(y_i=1|x_i)$，属于类别0的概率为$q(y_i=0|x_i)=1-q(y_i=1|x_i)$，使用上式，可以得到logistic回归的损失函数，
$$\begin{gathered} L(y,f(x))=-\frac{1}{N}\sum _{i=1}^N[y_i\log q(y_i=1|x_i)+(1-y_i)\log q(y_i=0|x_i)] \\ =-\frac{1}{N}\sum _{i=1}^N[y_i\log q(y_i=1|x_i)+(1-y_i)\log (1-q(y_i=1|x_i))] \end{gathered}$$

2.4 梯度下降算法

2.4.1 梯度下降算法原理

对于一个多元函数，梯度定义为对其中每个自变量的偏导数构成的向量，用$f^{{}^{\prime }}(x\text{x}x)$,
$$f^{{}^{\prime }}(x\text{x}x)=▽f(x\text{x}x)=[▽f({x\text{x}x}_1),...,▽f({x\text{x}x}_n){]}^T$$
考查$f(x\text{x}x+△x\text{x}x)$在$x\text{x}x$处的泰勒展开，如式(2.7)所示：
$$f(x\text{x}x+△x\text{x}x)=f(x\text{x}x)+f^{{}^{\prime }}(x\text{x}x{)}^T△x\text{x}x+o(△x\text{x}x)$$
忽略高阶项，要使得$f(x\text{x}x+△x\text{x}x)<f(x\text{x}x)$，就需要$f^{{}^{\prime }}(x\text{x}x{)}^T△x\text{x}x<0$，满足这个条件才能使函数值减小，进一步，$$f^{{}^{\prime }}(x\text{x}x{)}^T△x\text{x}x=||f^{{}^{\prime }}(x\text{x}x{)}^T||\cdot ||△x\text{x}x||\cdot \cos \theta$$，只需要取$△x\text{x}x=-\alpha f^{{}^{\prime }}(x\text{x}x)$，（使得$\cos \theta >0$）可保证更新后的$x\text{x}x$可以使得函数值减小，这里$\alpha 是一个超参数$，用于调整每次更新的步长，称为学习率。

机器学习的目标：最小化损失函数。

算法过程：

1. 随机初始化为需要求解的参数赋初值，作为优化起点；
2. 使用当前模型进行预测，计算损失值；
3. 利用损失值计算梯度，基于梯度更新参数。
4. 重复上述过程，直到达到停止条件。

2.4.2 梯度下降算法

全部样本计算损失函数的梯度：

给定训练集$\{x_n,y_n{\}}_{n=1}^N$，给定模型$f$，包含的参数集合为$\Theta =\{{\theta }^{(0)},...,{\theta }^{(k)}\}$，损失函数为$L(Y,f(X;\Theta ))$，学习率为$\alpha$。

随机初始化参数：$\{{\theta }_0^{(0)},...,{\theta }_0^{(k)}\}$
$$\begin{gathered} Fort=0,1,...,T: \\ {L}_t=L(Y,f(X;{\Theta }_t)), \\ ▽{\Theta }_t=\frac{\partial L_t}{\partial {\Theta }_t}=\{▽{\theta }_t^{(0)},...,▽{\theta }_t^{(k)}\} \\ {\Theta }_{t+1}=\{{\theta }_t^{(0)}-\alpha ▽{\theta }_t^{(0)},...,{\theta }_t^{(k)}-\alpha ▽{\theta }_t^{(k)}\} \end{gathered}$$
随机梯度下降算法:

由于全部样本在数据规模比较大的时候会十分低效，计算时间和计算复杂度都会增加，因此只使用单一样本来近似估计梯度可以提高效率。

小批量梯度下降算法：

因为随机梯度下降算法收敛速度很慢，因为其存在一定的不确定性，因此改进方法是每次使用多个样本来估计梯度。算法过程如下：

给定训练集$\{x_n,y_n{\}}_{n=1}^N$，给定模型$f$，包含的参数集合为$\Theta =\{{\theta }^{(0)},...,{\theta }^{(k)}\}$，损失函数为$L(Y,f(X;\Theta ))$，学习率为$\alpha$，批处理大小B。

随机初始化参数：$\{{\theta }_0^{(0)},...,{\theta }_0^{(k)}\}$
$$\begin{gathered} Fort=0,1,...,T，随机打乱样本，依次从X，Y中选择B个样本 \\ 得到X_{B_t},Y_{B_t}: \\ {L}_t=L(Y_{B_t},f(X_{B_t};{\Theta }_t)), \\ ▽{\Theta }_t=\frac{\partial L_t}{\partial {\Theta }_t}=\{▽{\theta }_t^{(0)},...,▽{\theta }_t^{(k)}\} \\ {\Theta }_{t+1}=\{{\theta }_t^{(0)}-\alpha ▽{\theta }_t^{(0)},...,{\theta }_t^{(k)}-\alpha ▽{\theta }_t^{(k)}\} \end{gathered}$$

2.5 神经网络

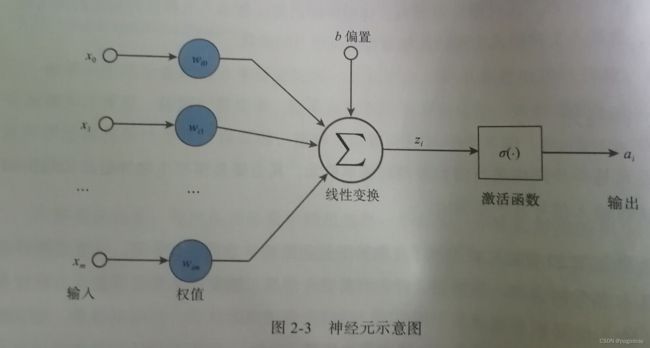
2.5.1 神经元

MP神经元模型：

$$\begin{gathered} z_i=\sum _{j=1}^m{w}_{ij}{x}_j \\ {a}_i=\sigma (z_i+b) \end{gathered}$$
其中$x_i$是输入信号，$w_{i0},w_{i1},w_{i2},...,w_{im}$是神经元的权值，$z_i$是输入信号的线性组合，b是偏置，激活函数是$\sigma (\cdot )$，$a_i$是神经元输出信号。

2.5.2 多层感知器

单隐层感知器典型结构：
$$f(x)=f_2(b^{(2)}+W^{(2)}(f_1(b^{(1)}+W^{(1)}x)))$$
其中$h(x)=f_1(b^{(1)})$是隐藏层的输出。b是偏置，W是权值向量，$f$是激活函数。

前馈神经网络——多层感知器（MLP）：隐藏层可以有多层。

注意：后一层的每个神经元与前一层的每个神经元都产生连接。
$$\begin{gathered} z^{(l)}=W^{(l)}\cdot {a\text{a}a}^{(l-1)}+{b\text{b}b}^{(l)} \\ {a\text{a}a}^{(l)}={\sigma }_l(z^{(l)}) \end{gathered}$$
整个网络可以表示为$\phi (X;W,b\text{b}b)$，其中$W,b\text{b}b$表示参数的集合$\{W^{(l)},{b\text{b}b}^{(l)}|l=1,2,3,...\}$。

2.5.3 激活函数

2.5.3.1 Sigmoid型函数

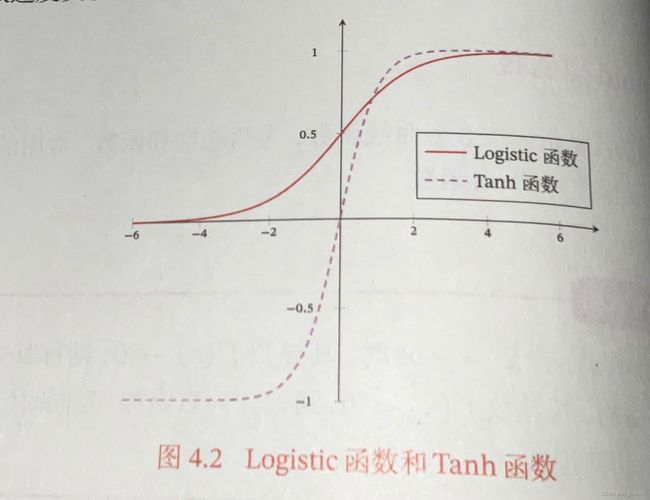
Sigmoid函数是指一类S型曲线函数，为两端饱和函数，常用的Sigmoid型函数有Logistic函数和Tanh函数。

所谓饱和，即当x趋近于负无穷时，其导数趋近于0，这时左饱和，右饱和亦是如此。

logistic函数：
$$\sigma (x)=\frac{1}{1+\exp (-x)}$$

Tanh函数：
$$\text{tanh}(x)=\frac{\exp (x)-\exp (-x)}{\exp (x)+exp(-x)}$$
Tanh函数可以看作放大并平移Logistic函数，其值域是(-1,1)。

logistic函数是非零中心化的，其输出恒大于0，它会使得其后一层的神经元的输入发生偏置偏移，并进一步使得收敛速度变慢。

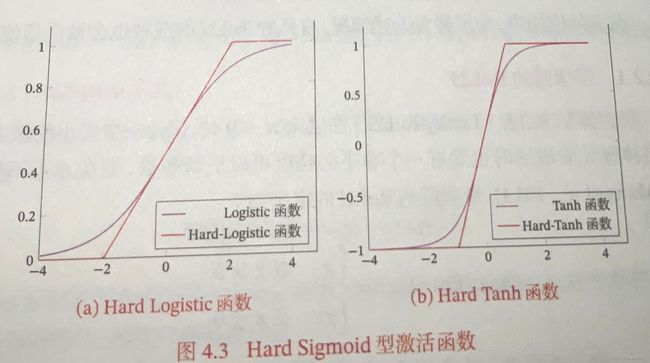
Hard-logistic和Hard-Tanh函数：

将Logistic函数进行泰勒展开有
$$g_l(x)\approx \sigma (x)+x\times {\sigma }^{{}^{\prime }}(x)$$
在x=0处展开可得
$$g_l(x)=0.25x+0.5$$
hard-logistic函数如下：
KaTeX parse error: No such environment: equation at position 8: \begin{̲e̲q̲u̲a̲t̲i̲o̲n̲}̲ \text{hard-log…

$$\text{hard-logistic}(x)=\max (\min (g_l(x),1),0)$$

同理，hard-tanh函数如下：
$$\begin{gathered} \text{hard-tanh(x)}=\max (\min (g_t(x),1),-1) \\ =\max (\min (x,1),-1) \\ 其中，g_t(x)=x \end{gathered}$$

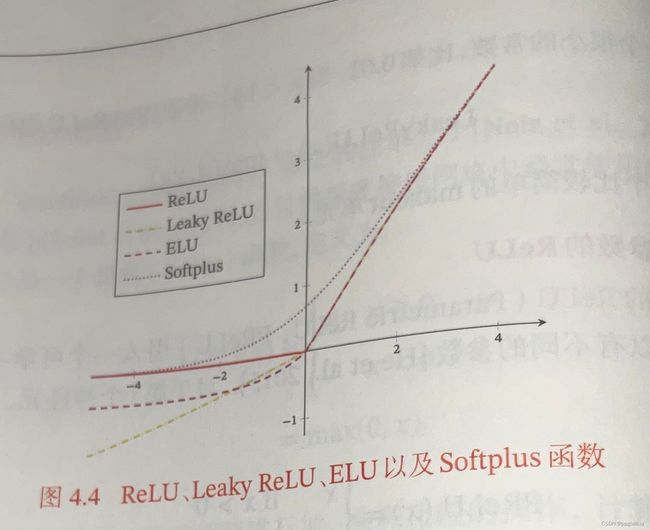
2.5.3.2 ReLU函数

ReLU（修正线性单元），也叫Rectifier函数，是目前深度神经网络中经常使用的激活函数。ReLU实际上是一个斜坡函数，即
KaTeX parse error: No such environment: equation at position 8: \begin{̲e̲q̲u̲a̲t̲i̲o̲n̲}̲ \text{ReLU}(x)…
优点：

1. ReLU的神经元只需要进行加、乘和比较的操作，计算ReLU函数也被认为具有生物合理性：单侧抑制，宽兴奋边界。同时人脑同一时刻只有少数神经元兴奋活跃，而Sigmoid型函数会导致一个非稀疏的神经网络，ReLU就具有稀疏性。
2. 同时在优化方面，ReLU是左饱和函数，x>0时，导数为1，在一定程度上缓解了神经网络的梯度消失问题。

缺点：

1. 非零中心化，后一层神经网络会引入偏置，降低梯度下降的效率；
2. 死亡ReLU问题，参数在一次不恰当的更新后，第一个隐藏层中的某个ReLU神经元所有的训练数据上都不能被激活，那么梯度将永远为0。为此，引入几个变种ReLU。

a.带泄露的ReLU

x<0时，保持一个小梯度，使得神经元在非激活状态也能更新参数，定义如下：
KaTeX parse error: No such environment: equation at position 8: \begin{̲e̲q̲u̲a̲t̲i̲o̲n̲}̲ \text {LeakyRe…
其中$\gamma$是一个很小的常数，比如0.01.

b.带参数的ReLU——PReLU

ReLU引入一个可学习的参数，不同神经元可以有不同的参数，对于第i个神经元，其PReLU的定义为
KaTeX parse error: No such environment: equation at position 9: \begin {̲e̲q̲u̲a̲t̲i̲o̲n̲}̲ \text{PReLU}_i…
PReLU可以允许不同神经元具有不同的参数，也可以一组神经元共享一个参数。如果$\gamma$为0，退化为ReLU；如果$\gamma$很小，退化为带泄露的ReLU。

2.5.3.3 ELU函数

ELU（指数线性单元）是一个近似的零中心化的非线性函数，其定义为
KaTeX parse error: No such environment: equation at position 9: \begin {̲e̲q̲u̲a̲t̲i̲o̲n̲}̲ ELU(x)= \begin…
$\gamma$是一个超参数，决定$x\le$时的饱和曲线，并调整输出均值在0附近。

2.5.3.4 Softplus函数

RelU的平滑版本，其定义为
$$\text{Softplus}(x)=\log (1+\exp (x))$$
其导数刚好是Logistic函数，Softplus函数虽然也具有单词抑制，宽兴奋边界的特性，却没有稀疏激活性。

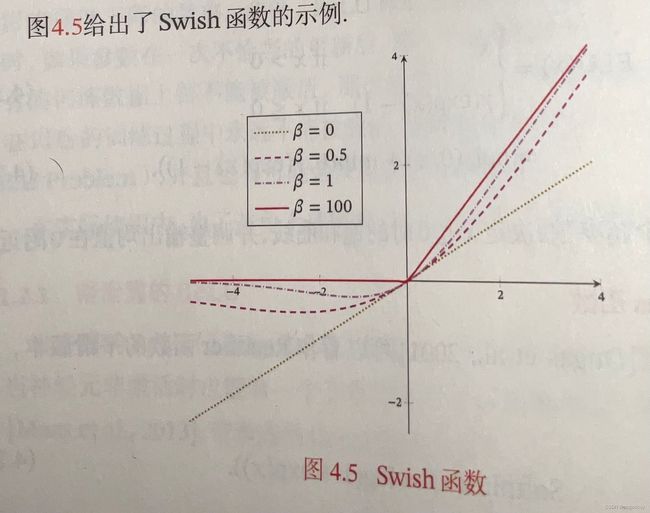
2.5.3.5 Swish函数

Swish函数是一种自门控激活函数，
$$\text{swish}(x)=x\sigma (\beta x)$$
其中，$\sigma (\cdot )$是logistic函数。$\beta$为可学习的参数或一个固定超参数。$\sigma (\beta x)$是一个软性的门控机制。当$\sigma (\beta x)$接近1时，门处于开，激活函数约等于x；当$\sigma (\beta x)$接近0时，门处于关，激活函数约等于0.

$\beta =0$的时候，Swish函数变成线性函数$x/2$;$\beta =1$时，Swish函数在$x>0$的时候近似线性，$x<0$的时候近似饱和，同时具有一定非单调性；$\beta =100$时，近似为ReLU函数。因此Swish函数可以看作线性函数和ReLU函数之间的非线性插值函数，其程度由参数$\beta$控制。

2.5.3.6 GELU函数（高斯误差线性单元）

是一种通过门控机制来调整其输出值的激活函数，和Swish函数比较类似。
$$\text{GELU}(x)=xP(X\le x)$$
其中$P(X\le x)$是高斯分布$N(\mu ,{\sigma }^2)$的累积分布函数，其中$\mu ,\sigma$为超参数，一般分别设置为0，1。由于高斯分布的累积分布函数是S型函数，因此GELU函数可以用Tanh函数或Logistic函数来近似，
$$\begin{gathered} \text{GELU}(x)\approx 0.5x(1+\text{tanh}(\sqrt{\frac{2}{\pi }}(x+0.044715x^3))) \\ or\approx x\sigma (1.702x) \end{gathered}$$
使用logistic函数近似时，GELU相当于一种特殊的Swish函数。

2.5.3.7 Maxout单元

Maxout单元也是一种分段线性函数，前面的净输入都是标量，而Maxout单元的输入是上一层神经元的全部原始输出，是一个向量。

每个Maxout有K个权重向量${w\text{w}w}_k\in {\mathbb{R}}^D$和偏置$b_k$.对于输入$x\text{x}x$，可以有K个净输入$z_k$.
$$z_k={w\text{w}w}_k^{T}x\text{x}x+b_k$$
其中，${w\text{w}w}_k=[w_{k,1},...,w_{k,D}{]}^T$为第k个权重向量。

Maxout单元的非线性函数定义为

$$\text{maxout}(x\text{x}x)=\underset{k\in [1,K]}{\max }(z_k)$$
Maxout单元不仅是净输入到输出之间的非线性映射，而是整体学习输入到输出之间的非线性映射关系。Maxout激活函数可以看做任意凸函数的分段线性近似，并且在有限的点上是不可微的。

2.5.4 训练神经网络

核心算法：反向传播算法

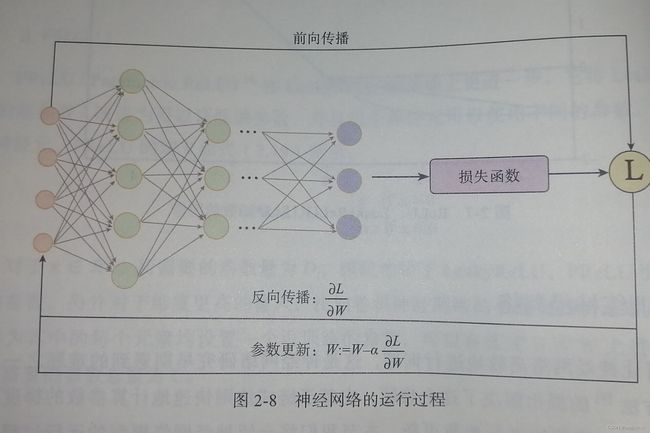
2.5.4.1 神经网络的运行过程

1. 前向传播：给定输入和参数，逐层向前进行计算，最后输出预测结果；
2. 反向传播：基于前向传播的预测结果，计算损失函数的值，然后计算相关参数的梯度。
3. 参数更新：使用梯度下降算法对参数进行更新，重复上述过程，逐步迭代到模型收敛。

2.5.4.2 反向传播

第$l$层的梯度计算如下，需要使用链式法则：
KaTeX parse error: Undefined control sequence: \part at position 8: \frac{\̲p̲a̲r̲t̲ ̲L(y,\hat y)}{\p…
定义KaTeX parse error: Undefined control sequence: \part at position 21: …a^{(l)}=\frac {\̲p̲a̲r̲t̲ ̲L(y,\hat y)}{\p…为误差项，它衡量的是$z^{(l)}$对损失值的影响，进一步使用链式法则，可得到如下
KaTeX parse error: Undefined control sequence: \part at position 21: …ta^{(l)}=\frac{\̲p̲a̲r̲t̲ ̲L(y,\hat y)}{\p…
基于$z^{(l+1)}=W^{(l+1)}{a\text{a}a}^{(l)}+{b\text{b}b}^{(l+1)}且{a\text{a}a}^{(l)}=\sigma (z^{(l)})$可以得到
KaTeX parse error: Undefined control sequence: \part at position 21: …ta^{(l)}=\frac{\̲p̲a̲r̲t̲ ̲L(y,\hat y)}{\p…
其中，$⨀$表示哈达玛积，可以看出第l层的误差与第l+1层的误差有关。

那么对于KaTeX parse error: Undefined control sequence: \part at position 8: \frac {\̲p̲a̲r̲t̲ ̲L(y,\hat y)}{\p…有，
KaTeX parse error: Undefined control sequence: \part at position 9: \frac {\̲p̲a̲r̲t̲ ̲L(y,\hat y)}{\p…

2.5.5 优化困境

梯度消失：

由于一般激活函数的导数${\sigma }^{{}^{\prime }}(x)<1$，例如sigmoid的导数最大值为0.25，当层数叠加时，多层的反向传播（连乘）会使得梯度值不断减小，接近输入层的梯度值非常小，参数几乎无法更新，在下一次前向传播时，就无法对后面的层产生较大的影响，模型难以有效训练。

因此现在的神经网络常用ReLU激活函数。

局部最优和鞍点：

损失函数通常是凸的，但是损失函数和参数之间的关系非凸。深度神经模型有很多局部最优点，当陷入局部最优的情况时，优化就会变得很困难，但是通常，这些局部最优点也能保证模型的效果。

另一个问题是由于维度过高，深度神经网络模型存在很多鞍点（在该处梯度为0），但它并不是最小值或者最大值，通常鞍点带来的挑战要比局部最优大很多。因为处于鞍点区域的时候，如果误差较大，由于这部分相对平坦，梯度值较小，模型收敛速度将受到极大影响，给人一种局部最优的假象。

,\hat y)}{\part z^{{(l)}}\=\delta}{(l)}
$$

2.5.5 优化困境

梯度消失：

由于一般激活函数的导数${\sigma }^{{}^{\prime }}(x)<1$，例如sigmoid的导数最大值为0.25，当层数叠加时，多层的反向传播（连乘）会使得梯度值不断减小，接近输入层的梯度值非常小，参数几乎无法更新，在下一次前向传播时，就无法对后面的层产生较大的影响，模型难以有效训练。

因此现在的神经网络常用ReLU激活函数。

局部最优和鞍点：

损失函数通常是凸的，但是损失函数和参数之间的关系非凸。深度神经模型有很多局部最优点，当陷入局部最优的情况时，优化就会变得很困难，但是通常，这些局部最优点也能保证模型的效果。

另一个问题是由于维度过高，深度神经网络模型存在很多鞍点（在该处梯度为0），但它并不是最小值或者最大值，通常鞍点带来的挑战要比局部最优大很多。因为处于鞍点区域的时候，如果误差较大，由于这部分相对平坦，梯度值较小，模型收敛速度将受到极大影响，给人一种局部最优的假象。