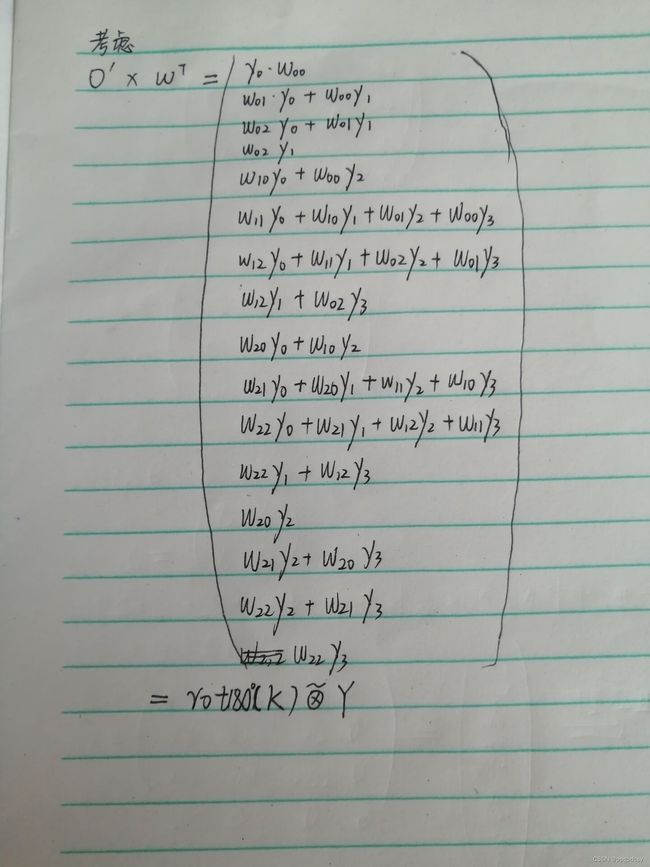《深入浅出图神经网络》读书笔记（3.卷积神经网络）

3.卷积神经网络

由于原书中对这一部分讲述并不详细，因此我参考邱锡鹏《深度学习和神经网络》以及各种资料进行详细地讲解，兄弟们认真读完一定会有收获的！

**卷积神经网络（CNN）**是一种具有局部连接、权重共享等特性的深层前馈神经网络。

用全连接前馈神经网络处理图像时会存在以下两个问题：

1. 参数太多：图像大小$100\ast 100\ast 3$，在第一个隐藏层的每个神经元到输入层都有30000个独立的连接，对应到相同的参数个数，随着隐藏层神经元数量的增多，参数急剧增加；
2. 局部不变性特征：自然界物体都具有局部不变性特征，比如尺度缩放、平移、旋转等操作不影响其语义信息，而全连接前馈神经网络很难提取这些特征，一般都需要数据增强来提高性能。

感受野：这是卷积神经网络的启发，是来自于生物学上的感受野机制。主要指听觉、视觉等神经系统中一些神经元的特性，即神经元只接受其所支配的刺激区域内的信号。即一个区域对应一些特定的神经元。

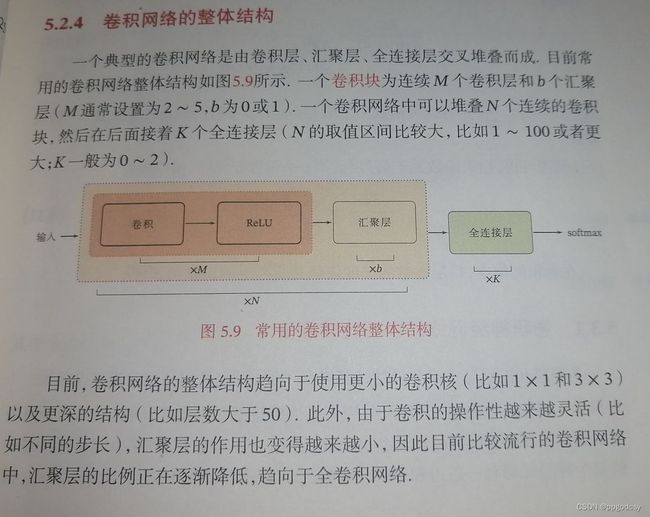
目前的卷积神经网络一般由卷积层、汇聚层核全连接层交叉堆叠而成的前馈神经网络。三个特性：局部连接、权重共享、汇聚。并很好地解决了上述两个问题。

5.1 卷积

5.1.1 卷积的定义

一维卷积：

卷积核大小：K

则信号序列$x\text{x}x$和卷积核$w\text{w}w$的卷积定义为
$$\begin{gathered} y\text{y}y=w\text{w}w\ast x\text{x}x \\ {y}_t=\sum _{k=1}^K{w}_k{x}_{t-k+1},下标t从K开始 \end{gathered}$$
二维卷积：

给定一个图像$X\text{X}X\in {\mathbb{R}}^{M\times N}$和一个卷积核$W\text{W}W\in {\mathbb{R}}^{U\times V}$，一般$U<<M,V<<N$，其卷积为
$$\begin{gathered} y_{ij}=\sum _{u=1}^U\sum _{v=1}^V{w}_{uv}{x}_{i-u+1,j-v+1},y_{ij}下标从(U,V)开始。 \\ 输入信息X\text{X}X和滤波器W\text{W}W的二维卷积定义为 \\ Y\text{Y}Y=W\text{W}W\ast X\text{X}X \end{gathered}$$

5.1.2 互相关

在图像处理领域，卷积的主要功能是在一个图像（或某种特征）上滑动一个卷积核，通过卷积操作得到一组新特征，计算过程中需要翻转。互相关是一个衡量两个序列相关性的函数，通常是用滑动窗口的点积计算来实现，给定一个图像$X\in {\mathbb{R}}^{M\times N}和卷积核W\text{W}W\in {\mathbb{R}}^{U\times V}$，它们的互相关如下
$$y_{ij}=\sum _{u=1}^U\sum _{v=1}^V{w}_{uv}{x}_{i+u-1,j+v-1},$$
与卷积的区别在于互相关不会翻转，因此互相关也叫不翻转卷积。可以写成如下形式
$$Y\text{Y}Y=W\text{W}W\otimes X\text{X}X=\text{rot180}(W\text{W}W)\ast X\text{X}X$$
$\otimes$为互相关运算，rot180表示旋转180度，$Y\text{Y}Y\in {\mathbb{R}}^{M-U+1,N-V+1}$.

5.1.3 卷积的变种

神经元计算公式：
$$(M-K+2P)/S+1$$
卷积核：$K\ast K$,K一般是奇数，原因如下：

（1）更容易padding

在卷积时，我们有时候需要卷积前后的尺寸不变。这时候我们就需要用到padding。假设图像的大小，也就是被卷积对象的大小为$n\ast n$，卷积核大小为$k\ast k$，padding的幅度设为$(k-1)/2$时，卷积后的输出就为$(n-k+2\ast ((k-1)/2))/1+1=n$，即卷积输出为$n\ast n$，保证了卷积前后尺寸不变。但是如果k是偶数的话，$(k-1)/2$就不是整数了。

（2）更容易找到卷积锚点

在CNN中，进行卷积操作时一般会以卷积核模块的一个位置为基准进行滑动，这个基准通常就是卷积核模块的中心。若卷积核为奇数，卷积锚点很好找，自然就是卷积模块中心，但如果卷积核是偶数，这时候就没有办法确定了，让谁是锚点似乎都不怎么好。

5.1.4 卷积的数学性质

宽卷积的定义，给定一个二维图像$X\text{X}X\in {\mathbb{R}}^{M\times N}$和一个二维卷积核$W\in {\mathbb{R}}^{U\times V}$，对图像进行零填充，两端各补U-1和V-1个0，得到全填充的图像$\widetilde{X\text{X}X}\in {\mathbb{R}}^{(M+2U-2)\times (N+2V-2)}$，定义如下：
$$W\text{W}W\tilde{\otimes }X\text{X}X\triangleq W\text{W}W\otimes \widetilde{X\text{X}X}$$
$\tilde{\otimes }$表示宽卷积运算，当输入信息和卷积核有固定长度时，它们的宽卷积依然具有交换性，即
$$\text{rot180}(W\text{W}W)\tilde{\otimes }X\text{X}X=\text{rot180}(X\text{X}X)\tilde{\otimes }W\text{W}W$$
导数

5.2 卷积神经网络

一般由卷积层、汇聚层和全连接层构成。

5.2.1 用卷积代替全连接

用卷积代替全连接可以解决参数过多的问题。
$${z\text{z}z}^{(l)}={w\text{w}w}^{(l)}\otimes {a\text{a}a}^{(l-1)}+b^{(l)}$$
其中，${w\text{w}w}^{(l)}\in {\mathbb{R}}^K$为可学习的权重向量，$b^{(l)}\in \mathbb{R}$为可学习的偏置。

局部连接：在卷积层(l层)中的每一个神经元都只和前一层(第l-1层)中某个局部窗口内的神经元相连，构成一个局部连接网络。

权重共享：作为参数的卷积核${w\text{w}w}^{(l)}$对于第l层的所有的神经元都是相同的。

由于上述两种特性，卷积层的参数只有一个K维的权重向量和1维的偏置，共K+1个参数。第l层的神经元个数为$M_l=M_{l-1}-K+1$。

5.2.2 卷积层

不失一般性，卷积层的结构如下：

1. 输入特征映射组：$X\in {\mathbb{R}}^{M\times N\times D}$为三维张量，其中每个切片矩阵${X\text{X}X}^d\in {\mathbb{R}}^{M\times N}$为一个输入特征映射，$1\le d\le D$;

2. 输出特征映射组：$Y\in {\mathbb{R}}^{M^{{}^{\prime }}\times N^{{}^{\prime }}\times P}$为三维张量，其中每个切片矩阵${Y\text{Y}Y}^p\in {\mathbb{R}}^{M^{{}^{\prime }}\times N^{{}^{\prime }}}$为一个输入特征映射，$1\le p\le P$;

3. 卷积核：$W\in {\mathbb{R}}^{U\times V\times P\times D}$为四维张量，其中每个切片矩阵${W\text{W}W}^{p,d}\in {\mathbb{R}}^{U\times V}$为一个二维卷积核，$1\le d\le D，1\le p\le P$。

一共需要参数个数：

对于每个卷积核${W\text{W}W}^p$:$U\times V$

对于一个输出：$(U\times V)\ast D+1$

一共有P个输出：$(U\times V)\ast D\ast P+P$.

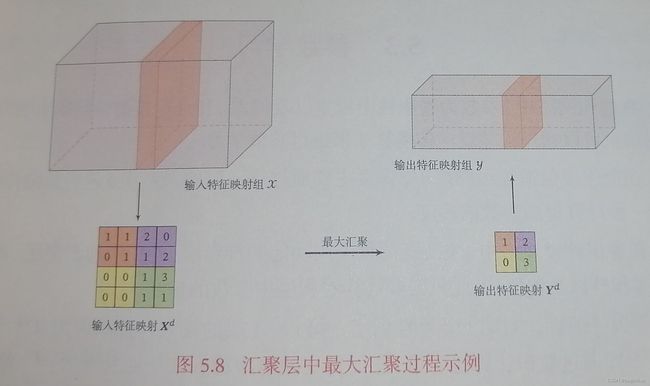
5.2.3 汇聚层（池化层）

也叫子采样层，作用：进行特征选择，降低特征数量，从而减少参数数量。

卷积层无法减少神经元数量，造成输入维度数很高，容易出现过拟合，而卷积层后面加上汇聚层来降低特征维数，就可以避免过拟合。

假设汇聚层的输入特征映射组成为$X\text{X}X\in {\mathbb{R}}^{M\times N\times D}$，其中每一个特征映射$X\text{X}X\in {\mathbb{R}}^{M\times N},1\le d\le D$,将其划分为很多区域$R_{m,n}^d,1\le m\le M^{{}^{\prime }},1\le n\le N^{{}^{\prime }}$，这些区域可以重叠也可以不重叠，汇聚即对每个区域进行下采样得到一个值，一般由两种方式：

1. 最大汇聚：选出最大的活性值作为这个区域的表示；
2. 平均汇聚：取区域内所有活性值的平均值。

最终得到汇聚映射${Y\text{Y}Y}^d$.

可以看出，汇聚层可以有效减少神经元的数量，还可以使得网络对一些小的局部形态改变保持不变性，并拥有更大的感受野。

除了使用下采样操作，还可以使用非线性激活函数，如LeNet-5。同时汇聚层也可以看作一个特殊的卷积层，卷积核大小为$K\times K$,步长$S\times S$,卷积核为max或者mean函数。

5.2.4 卷积网络的整体结构

5.3 参数学习

前馈计算
$$\begin{gathered} {Z\text{Z}Z}^{(l,p)}=\sum _{d=1}^D{W\text{W}W}^{(l,p,d)}\otimes {X\text{X}X}^{(l-1,d)})+b^{(l,p)} \\ {X\text{X}X}^{(l,d)}={a\text{a}a}^{(l-1,p)}=\sigma ({Z\text{Z}Z}^{(l-1,p)}),此时d=p，因为上层输出的维数等于下一层的输入维数 \end{gathered}$$
卷积神经网络的反向传播算法：

首先使用链式法则：根据根据5.1.4第一个导数公式可得
$$\begin{gathered} \frac{\partial L}{\partial {W\text{W}W}^{(l,p,d)}}=\frac{\partial L}{\partial {Z\text{Z}Z}^{(l,p)}}\otimes {X\text{X}X}^{(l-1,d)} \\ 其中，{\delta }^{(l,p)}=\frac{\partial L}{\partial {Z\text{Z}Z}^{(l,p)}}为损失函数关于第l层的第p个特征映射净输入Z^{(l,p)}的偏导数。 \\ \frac{\partial L}{\partial b^{(l,p)}}=\sum _{i,j}[{\delta }^{(l,p)}{]}_{i,j} \\ 之所以求和，是因为{\delta }^{(l,p)}和b维度不匹配，通常使用求和来解决这个问题。 \end{gathered}$$
汇聚层：

当第l+1层是汇聚层的时候，如果已知${\delta }^{(l+1,p)}$，由于汇聚层是进行了下采样操作，因此对${\delta }^{(l+1,p)}$进行一次上采样即可得到
$$\frac{\partial L}{\partial {a\text{a}a}^{(l,p)}}=\frac{\partial L}{\partial {X\text{X}X}^{(l+1,p)}}=up({\delta }^{(l+1,p)})$$
再和l层的特征映射的激活值偏导数逐元素相乘，整体推导如下
$$\begin{gathered} {\delta }^{(l,p)}=\frac{\partial L}{\partial {Z\text{Z}Z}^{(l,p)}}=\frac{\partial {a\text{a}a}^{(l,p)}}{{Z\text{Z}Z}^{(l,p)}}\cdot \frac{\partial L}{\partial {a\text{a}a}^{(l,p)}} \\ =f_l^{{}^{\prime }}({Z\text{Z}Z}^{(l,p)})\odot up({\delta }^{(l+1,p)}) \\ 其中，f_l为l层使用的激活函数，up为上采样 \end{gathered}$$
上采用的两种方法：

1. 下采样是最大汇聚的时候，将误差项${\delta }^{(l+1,p)}$中每个值直接传递导前一层对应区域中的最大值所对应的神经元，其它均设为0.
2. 下采样是平均汇聚的时候，将误差项每个值都平均分配到前一层对应区域的所有神经元上。

卷积层：

当l+1层是卷积层的时候，推导过程如下（根据5.1.4第二个导数公式）
$$\begin{gathered} {\delta }^{(l,p)}=\frac{\partial L}{\partial {Z\text{Z}Z}^{(l,p)}}=\frac{\partial {a\text{a}a}^{(l,p)}}{{Z\text{Z}Z}^{(l,p)}}\cdot \frac{\partial L}{\partial {a\text{a}a}^{(l,p)}} \\ =\frac{\partial {X\text{X}X}^{(l+1,p)}}{{Z\text{Z}Z}^{(l,p)}}\cdot \frac{\partial L}{\partial {X\text{X}X}^{(l+1,p)}} \\ =f_l^{{}^{\prime }}({Z\text{Z}Z}^{(l,p)})\odot \sum _{P=1}^P(\text{rot180}({W\text{W}W}^{(l+1,p,d)})\tilde{\otimes }\frac{\partial L}{\partial {Z\text{Z}Z}^{(l+1,p)}}) \\ =f_l^{{}^{\prime }}({Z\text{Z}Z}^{(l,p)})\odot \sum _{P=1}^P(\text{rot180}({W\text{W}W}^{(l+1,p,d)})\tilde{\otimes }{\delta }^{(l+1,p)}) \end{gathered}$$
$\tilde{\otimes }$是宽卷积。

5.4 几种典型的卷积神经网络

5.4.1 LeNet-5

LeNet-5共有7层，假设输入图像大小为$32\times 32=1024$，输出对应10个类别的得分；

C1卷积层：使用6个$5\times 5$的卷积核，得到6组大小为$28\times 28=784$的特征映射，因此，C1层的神经元数量为$6\times 784=4704$，可训练参数数量为$6\times 25+6=156$个，连接数量为$156\times 784=122304$.

S2汇聚层：采样窗口$2\times 2$，使用平均汇聚，并使用非线性激活函数${Y\text{Y}Y}^{{}^{\prime }d}=f(w^d{Y\text{Y}Y}^d+b^d)$,其中${Y\text{Y}Y}^{{}^{\prime }d}$为汇聚层的输出，$f$为非线性激活函数，$w^d和b^d$是可学习的标量权重和偏置。神经元个数$6\times 14\times 14=1176$，可训练参数$6\times (1+1)=12$，连接数为$6\times 196\times (4+1)=5880$，+1表示非线性激活函数的计算。

C3卷积层：LeNet-5中用一个连接表来定义输入和输出特征映射之间的依赖的关系，如下图，共使用60个$5\times 5$的卷积核，得到16组$10\times 10$的特征映射。神经元1600个，可训练参数个数$(60\times 25)+16=1516个$，连接数$1516\times 100=151600$。

这样只需要60个卷积核（上图中X的数量），C3层的第0-5个特征映射依赖于S2层的特征映射组的每3个连续子集，以此类推。如果不使用连接表，那么需要96个$5\times 5$的卷积核。

如果第p个输出特征映射依赖于第d个输入特征映射，则$T_{p,d}=1$，否则为0.那么
$${Y\text{Y}Y}^p=f(\sum _{d,T_{p,d}=1}{W\text{W}W}^{p,d}\otimes {X\text{X}X}^d+b^p)$$
其中T为$P\times D$的连接表，假设连接表的非零个数为K，每个卷积核大小为$U\times V$,那么参数个数为$K\ast (U\times V)+P$.

S4汇聚层：采样窗口为$2\times 2$，得到16个$5\times 5$的特征映射，可训练参数数量为$16\times 2$=32，连接数为$16\times 25\times (4+1)=2000$.

C5卷积层：使用$120\times 16=1920$个$5\times 5$的卷积层得到120组$1\times 1$的特征映射，C5神经元数量为120，可训练参数数量为$1920\times 25+120=48120$,连接数为$120\times (16\times 5\times 5+1)=48120$个。

F6全连接层，84个神经元，共$84\times (120+1)=10164$个参数，连接数与参数数量相同。

输出层：10个径向基函数（RBF）组成，分别代表每一类的得分。对于手写字符系统来讲，可以把手写字符的比特图看作84个节点，看输入输出的差别程度。

5.4.2 AlexNet

第一个现代深度卷积网络，其可以使用GPU进行并行训练，采用ReLU作为非线性激活函数，使用Dropout防止过拟合，使用数据增强来提高模型准确率等现代深度卷积网络的技术方法。

Alex的结构包括5个卷积层，3个汇聚层和3个全连接层，最后一层是使用Softmax函数的输出层，因为网络规模超出了当时的单个GPU的内存限制，AlexNet将网络拆为两半，分别放在两个GPU上，GPU间只在某些层（比如第三层）进行通信。

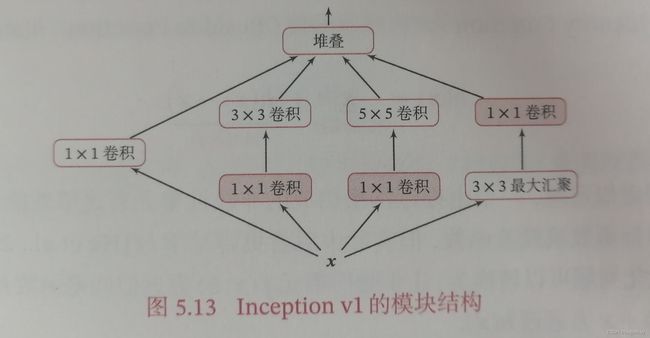
5.4.3 Inception网络

在卷积网络中，如何设置卷积层的卷积核大小是一个非常关键的问题，在Inception网络中，一个卷积层包含多个不同大小的卷积操作，称为Inception模块。

Inception网络是由多个Inception模块和少量的汇聚层堆叠而成。

Inception v1的模块结构：

这里的$1\times 1$卷积核的深度与输入的特征映射的深度是相同的，这样可以设定$1\times 1\times \text{depth}$的输出通道数来控制特征映射的深度，相当于一次特征抽取；同时也可以将$1\times 1$卷积核看作一种全连接，举个例子：

输入特征映射$W\times H\times D$，那么卷积核$1\times 1\times D\times \text{outchannels} $。假如D=6，outchannels=5，就可以看做如下所示的全连接：

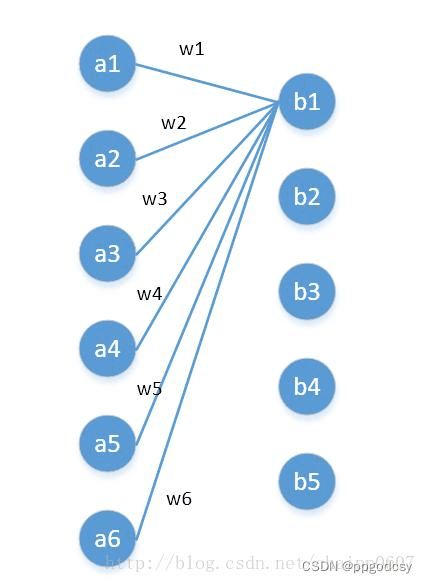
image from:http://blog.csdn.net/chaipp0607

由上述可知，$1\times 1$的卷积核可以通过降低特征映射的深度来**减少计算量。**例子如下：

卷积核参数计算：$卷积核的长度\ast 卷积核的宽度\ast 卷积核的个数$

卷积计算量计算：$输出数据大小\ast 卷积核的尺寸\ast 输入通道数（卷积的第三个维度）$

运算量：$5\ast 5\ast 192\ast 28\ast 28\ast 32=120M$

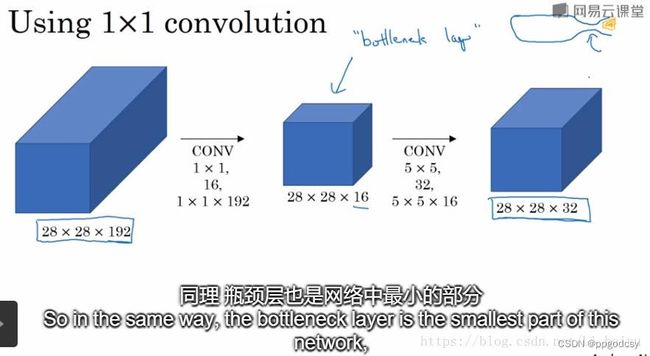
image from:http://blog.csdn.net/Li_haiyu

运算量：$28\ast 28\ast 32\ast 5\ast 5\ast 16+1\ast 1\ast 192\ast 28\ast 28\ast 16=12.4M$

e.g. GoogLeNet

GoogLeNet由9个Inception v1模块和5个汇聚层以及其他一些卷积层和全连接层构成，总共22层网络。

并且为了解决梯度消失问题，GoogLeNet在网络中间层引入了两个辅助分类器来加强监督信息。

e.g. Inception v3

Inception v3用多层小卷积核来替换大的卷积核来减少计算量和参数量，并保持感受野不变。具体包括：

1. 使用两层$3\times 3$的卷积来替换v1中的$5\times 5$的卷积；
2. 使用连续的$K\times 1$和$1\times K$来替换$K\times K$的卷积；
3. 引入了标签平滑以及批量归一化等优化方法进行训练。

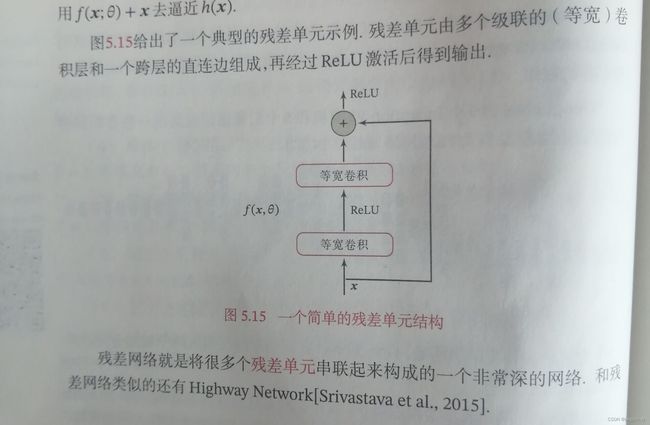
5.4.4 残差网络

残差网络通过给非线性的卷积层增加直连边的方式(也称为残差连接)来提高信息的传播效率。

其主要思想是：当我们用一个非线性单元（一层或多层卷积层）$f(x\text{x}x;\theta )$去逼近一个目标函数为$h(x\text{x}x)$.如果将目标函数拆分如下
$$h(x\text{x}x)=x\text{x}x+(h(x\text{x}x)-x\text{x}x)=恒等函数+残差函数$$
实际过程中，更容易学习残差函数，因此原来的优化问题转化为：让线性单元$f(x\text{x}x;\theta )$去近似残差函数$h(x\text{x}x)-x\text{x}x$,用$f(x\text{x}x;\theta )+x\text{x}x$去逼近目标函数。

残差单元结构：

优势如下：前向传播时，将输入与输出的信息进行融合，能够更有效地利用特征；二是在反向传播时，总有一部分梯度通过跳跃连接反传到输入上，缓解了梯度消失的问题。

5.4.5 VGG网络

5.5 其它卷积方式

除了变种的卷积，还有几种其它卷积方式。

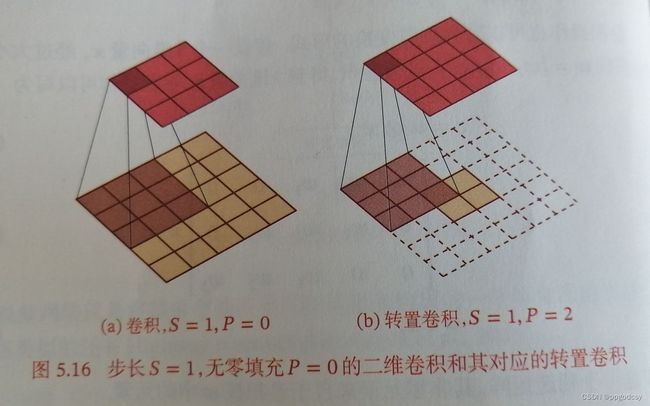
5.5.1 转置卷积

卷积操作一般实现高维特征到低维特征的转换，因此我们需要一种可以看作“反卷积”的方式，来实现低维特征到高维特征的转换，这就是转置卷积。

在卷积操作中，是多对一的关系。而在转置卷积中，应该是一对多的关系，如下图所示：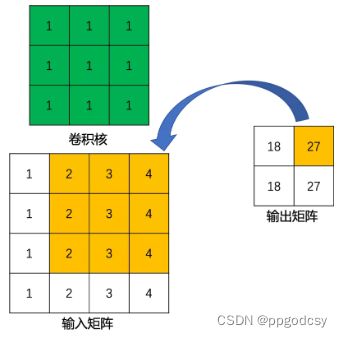

当然，从信息论的角度上看，常规卷积操作是不可逆的，所以转置卷积并不是通过输出矩阵和卷积核计算原始输入矩阵，而是计算得到保持了相对位置关系的矩阵。from：https://blog.csdn.net/qq_39478403/article/details/121181904

前置计算和反向传播就是一种转置关系。

转置卷积的推导

http://imgtec.eetrend.com/blog/2019/100018318.html

https://blog.csdn.net/qq_39478403/article/details/121181904

推导精炼如下：

无零填充时S=1对应的二维卷积和转置卷积：

微步卷积

$S>1$的时候，我们一般进行下采样；$S<1$的时候，我们实现上采样。因此步长$S<1$的转置卷积也叫微步卷积。如果步长为$\frac{1}{S},S>1$,那么需要在特征之间插入$S-1$个0.如下图：

5.5.2 空洞卷积

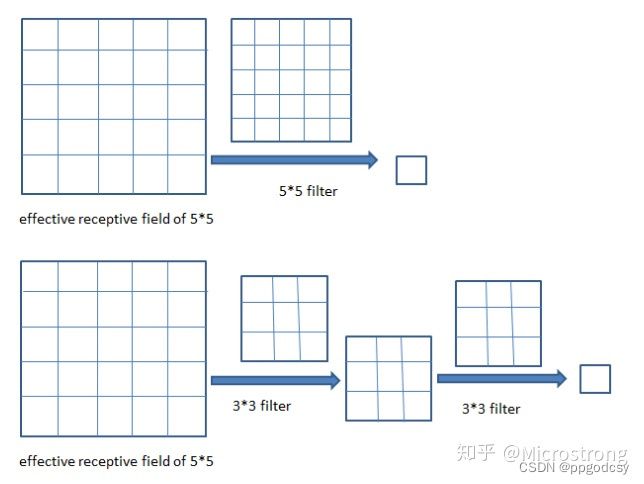
对于一个卷积层，如果希望增加输出单元的感受野，一般可以通过三种方式实现：

1. 增加卷积核的大小；

2. 增加层数，比如两层$3\times 3$的卷积可以近似一层$5\times 5$的卷积，如下图：

3. 卷积前进行汇聚，前两者会增加参数数量，而第三种方式会丢失一种信息。

空洞卷积可以不增加参数数量同时增加输出单元感受野的一种方法，也叫膨胀卷积。其方法是给卷积核插入空洞来变相增加卷积核大小，新的卷积核大小公式如下：
$$K^{{}^{\prime }}=K+(K-1)\times (D-1)$$
D为膨胀率，为1时就是普通的卷积核，为2时就是带有空洞的$5\times 5$卷积核（若原来卷积核大小为3）。

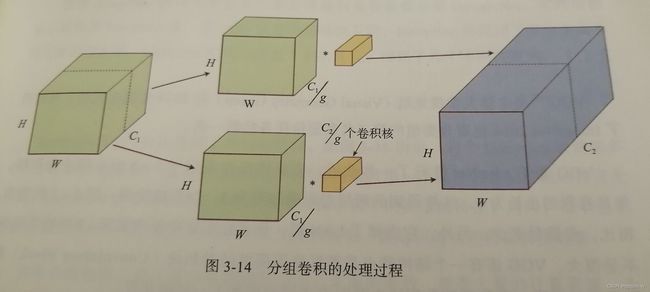
5.5.3 分组卷积

分组卷积最早是在AlexNet中出现，当时训练AlexNet时卷积操作不能全部放在同一个GPU中进行处理，因此作者把特征图分给了多个GPU来处理，这实际上就是分组卷积，示意图如下：

输入沿着深度方向划分为g组，每一组由$C_1/g$个通道构成，同理输出沿着深度方向划分为g组，每一组由$C_2/g$个通道构成，将输入输出对应起来，分别使用卷积（卷积的深度为$C_2/g$）进行计算。

这样卷积核大小为$K\times K\times \frac{C_1}{g}\times \frac{C_2}{g}$，深度和卷积核的个数都得到了减少，最后拼接输出，需要的参数为$(K\times K\times \frac{C_1}{g}\times \frac{C_2}{g})\times g$，参数量减少g倍。

5.5.4 深度可分离卷积

由两部分组成，一部分是沿着深度的逐层卷积，另一部分是$1\times 1$卷积，沿着深度的逐层卷积是分组卷积的一种特殊情况，当$g=C_1=C_2$时，它相当于为每一个输入通道设定了一个卷积核分别进行卷积。

由于这种卷积只使用了单个输入通道的信息，即空间位置上的信息，没有使用通道之间的信息，其后通常使用$1\times 1$卷积来增加通道间信息。

这种卷积相比较于标准卷积，可以减少参数量、计算量并且提高运算效率。MobileNet、ShuffleNet等模型上都有应用。

5.6 感受野的计算

from:https://blog.csdn.net/qq_41076797/article/details/114434415#_10

补充

batchnorm：

为了加快神经网络收敛速度而设计的方法，核心思想在于梯度下降时要避免大特征淹没小特征的情况，因此每一次都要对输出进行正则化，这种正则化是需要恢复的，不然学习到的数据特征将是无效的。
这种卷积相比较于标准卷积，可以减少参数量、计算量并且提高运算效率。MobileNet、ShuffleNet等模型上都有应用。