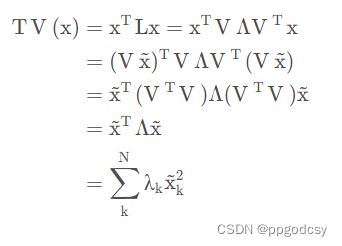《深入浅出图神经网络》读书笔记(5.图信号处理与图卷积神经网络)
5.图信号处理与图卷积神经网络
5.1 矩阵乘法
5.2 图信号与图的拉普拉斯矩阵
图 G = ( V , E ) G=(V,E) G=(V,E),共有N个节点,图信号是一种描述 V → R V\rightarrow R V→R的映射,可以表示为向量 x = [ x 1 , x 2 , . . . , x N ] T \pmb x=[x_1,x_2,...,x_N]^T xxx=[x1,x2,...,xN]T,其中 x i x_i xi表示的是节点 v i v_i vi上的信号强度。
拉普拉斯矩阵: L = D − A L=D-A L=D−A,D为一个对角矩阵,对角线元素为节点度数,A则是邻接矩阵
L { deg ( v i ) , if i=j − 1 , if e i j ∈ E 0 , otherwise L \begin{cases} \text{deg}(v_i),\quad \text{if\quad i=j} \\ -1 ,\quad \text{if}\quad e_{ij}\in E \\ 0 , \quad \text{otherwise} \end{cases} L⎩⎪⎨⎪⎧deg(vi),ifi=j−1,ifeij∈E0,otherwise
可以正则化表示为 L sym = D − 1 2 L D − 1 2 L_{\text{sym}}=D^{-\frac {1}{2}}LD^{-\frac {1}{2}} Lsym=D−21LD−21,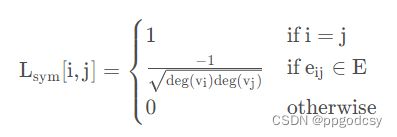
这是GCN的关键。
考虑拉普拉斯算子,将该算子的作用域退化到离散的二维图像空间,就是边缘检测算子:
△ f ( x , y ) = f ( x + 1 , y ) + f ( x − 1 , y ) + f ( x , y + 1 ) + f ( x , y − 1 ) − 4 f ( x , y ) \triangle f(x,y)=f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)-4f(x,y) △f(x,y)=f(x+1,y)+f(x−1,y)+f(x,y+1)+f(x,y−1)−4f(x,y)
矩阵形式如下
KaTeX parse error: Unknown column alignment: 0 at position 23: … \begin{array}{0̲} 0&1&0 \\ 1& -…
具体的扩展可以参考:https://blog.csdn.net/hellocsz/article/details/102485387
拉普拉斯算子可以用来描述中心节点与邻居节点之间的信号的差异:
L x = [ . . . , ∑ v j ∈ N ( v i ) ( x i − x j ) , . . . ] L\pmb x=[...,\sum_{v_j\in N(v_i)}(x_i-x_j),...] Lxxx=[...,vj∈N(vi)∑(xi−xj),...]
二次型:
x T L x = ∑ v i ∑ v j ∈ N ( v i ) x i ( x i − x j ) = ∑ e i j ∈ E ( x i − x j ) 2 \pmb x^TL\pmb x=\sum_{v_i} \sum_{v_j\in N(v_i)}x_i(x_i-x_j)\\=\sum_{e_{ij\in E}}(x_i-x_j)^2 xxxTLxxx=vi∑vj∈N(vi)∑xi(xi−xj)=eij∈E∑(xi−xj)2
令上式为TV(x),即图信号的总变差。它是一个标量,将各条边上的差值进行加和,刻画了图信号整体的平滑度。
5.3 图傅里叶变换
显然L是一个实对称矩阵,其可以被正交对角化
L = V Λ V T L=V\Lambda V^T\\ L=VΛVT
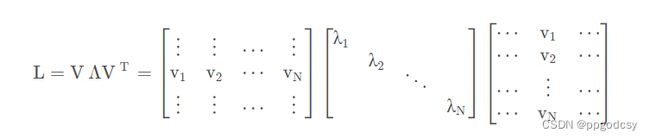
其中V是一个 N × N N\times N N×N的正交矩阵,且有 V V T = I VV^T=I VVT=I. V = [ v 1 , v 2 , . . . , v N ] V=[\pmb v_1,\pmb v_2,...,\pmb v_N] V=[vvv1,vvv2,...,vvvN],表示L的N个特征向量,这些特征向量线性无关。 λ k \lambda_k λk表示第k个特征向量 v k \pmb v_k vvvk的特征值,升序排列,即 λ 1 ≤ λ 2 ≤ . . . ≤ λ N \lambda_1\le\lambda_2\le...\le\lambda_N λ1≤λ2≤...≤λN。
拉普拉斯矩阵的二次型 x T L x \pmb x^TL\pmb x xxxTLxxx显然是大于等于0的,因此拉普拉斯矩阵是一个半正定型矩阵,其所有的特征值均大于等于0.当 x \pmb x xxx为全为1的向量时, L x = 0 L\pmb x=0 Lxxx=0,因此拉普拉斯矩阵最小的特征值为0,即 λ 1 = 0 \lambda_1=0 λ1=0。
同时对于 L s y m L_{sym} Lsym,其特征值有上限 λ N ≤ 2 \lambda_N\le2 λN≤2.
图傅里叶变换(GFT):
x ~ k = ∑ i = 1 N V k i T x i = < v k , x > \tilde x_k=\sum_{i=1}^NV_{ki}^Tx_i=<\pmb v_k,\pmb x> x~k=i=1∑NVkiTxi=<vvvk,xxx>
特征向量为傅里叶基, x ~ k \tilde x_k x~k是 x \pmb x xxx在第k个傅里叶基上的傅里叶系数,傅里叶系数本质上是图信号在傅里叶基上的投影,衡量了图信号与傅里叶基之间的相似度:
x ~ = V T x , x ~ ∈ R N \tilde{\pmb x}=V^T\pmb x,\tilde {\pmb x}\in R^N xxx~=VTxxx,xxx~∈RN
由于V是一个正交矩阵,对上式左乘V,则: V x ~ = V V T x = x V\tilde {\pmb x}=VV^T\pmb x=\pmb x Vxxx~=VVTxxx=xxx.因此逆图傅里叶变换(IGFT):
x k = ∑ i = 1 N V k i ⋅ x ~ i x = ∑ k = 1 N x ~ k ⋅ v k x_k=\sum_{i=1}^NV_{ki}\cdot\tilde x_i\\ \pmb x=\sum_{k=1}^N\tilde x_k\cdot\pmb v_k xk=i=1∑NVki⋅x~ixxx=k=1∑Nx~k⋅vvvk
这表明傅里叶基是一组完备的基向量,任意一个图信号都可以被这组基所表示。
总变差是图的所有特征值的线性组合,其权重是对应的傅里叶系数的平方。
总变差是用来刻画图信号的平滑度的,图信号越平滑,其总变差就会越小。所谓图信号的平滑度就是整张图中相邻近的图信号之间的变化程度。总变差大一些,图中的信号变化就会更剧烈。由这个观点,我们是要去寻求总变差最小的图。那么由于各个特征向量彼此正交,且特征值升序排列,因此图信号就应该与 λ 1 \lambda_1 λ1对应的特征向量完全重合,此时仅有 x 1 ≠ 0 \pmb x_1\ne0 xxx1=0,其它傅里叶系数均为0, T V ( v 1 ) = λ 1 TV(\pmb v_1)=\lambda_1 TV(vvv1)=λ1.
进一步(需要证明,已有结论),如果要选择一组彼此正交的图信号,使得各自的总变差依次取得最小值,那么这组信号就是 v 1 , v 2 , . . . , v N \pmb v_1,\pmb v_2,...,\pmb v_N vvv1,vvv2,...,vvvN。
特征值其实是对图信号平滑度的一种梯度刻画,**因此可以将特征值等价于频率。**特征值越低,频率越低,对应的傅里叶基变化得越缓慢,相近节点越一致;特征值越高,频率越高,对应的傅里叶基变化得越剧烈,相近节点越不一致。
定义图信号的能量:
E ( x ) = ∣ ∣ x ∣ ∣ 2 2 = x x T = ( V x ~ ) T ( V x ~ ) = x ~ T x ~ E(\pmb x)=||\pmb x||_2^2=\pmb x\pmb x^T=(V\pmb {\tilde x})^T(V\pmb{\tilde x})=\tilde {\pmb x}^T\tilde {\pmb x} E(xxx)=∣∣xxx∣∣22=xxxxxxT=(Vx~x~x~)T(Vx~x~x~)=xxx~Txxx~
上式子可知,图信号的能量可以从空域和频域等价。既然频率是特征值,那么傅里叶系数可以等价为图信号在对应频率分量上的幅值。
图信号在低频分量上强度越大,图信号平滑度越高(变化更小);反之亦然。
傅里叶系数组合在一起称为频谱,是从频域研究图信号的根本。
5.4 图滤波器
图滤波器:对给定图信号的频谱中各个频率分量的强度进行增强或衰减的操作。假设 H ∈ R N × N , H : R N → R N H\in R^{N\times N},H:R^N\rightarrow R^N H∈RN×N,H:RN→RN,令输出信号为 y \pmb y yyy,则:
y = H x = ∑ k = 1 N ( h ( λ k ) x ~ k ) v k \pmb y=H\pmb x=\sum_{k=1}^N(h(\lambda_k)\tilde x_k)\pmb v_k yyy=Hxxx=k=1∑N(h(λk)x~k)vvvk
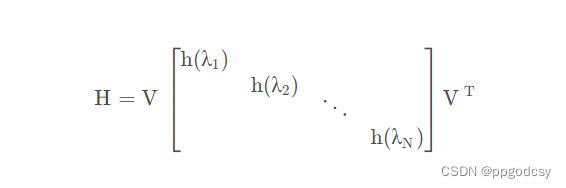
比起拉普拉斯矩阵,H仅仅改动了对角矩阵上的值,因此H的形式如下: H i j = 0 , 如 果 i ≠ j 或 者 e i j ∉ E H_{ij}=0,如果i\ne j或者e_{ij}\notin E Hij=0,如果i=j或者eij∈/E。 H x H\pmb x Hxxx描述了一种作用在每个节点一阶子图上的变换操作,一般我们称满足上述性质的矩阵H为G的图位移算子,拉普拉斯矩阵和邻接矩阵都是典型的图位移算子。
图滤波器的性质:
- 线性: H ( x + y ) = H x + H y H(\pmb x+\pmb y)=H\pmb x+H\pmb y H(xxx+yyy)=Hxxx+Hyyy;
- 滤波操作是顺序无关的: H 1 ( H 2 x ) = H 2 ( H 1 x ) H_1(H_2\pmb x)=H_2(H_1\pmb x) H1(H2xxx)=H2(H1xxx);
- 如果 h ( λ ) ≠ 0 , 则 该 滤 波 操 作 是 可 逆 的 h(\lambda)\ne 0,则该滤波操作是可逆的 h(λ)=0,则该滤波操作是可逆的。
Λ h \Lambda_h Λh为图滤波器H的频率响应矩阵,对应的函数 h ( λ ) h(\lambda) h(λ)为H的频率响应函数。不同的频率响应函数可以实现不同滤波效果:低通滤波器、高通滤波器、带通滤波器。
实现任意性质的图滤波器,也就是实现任意类型函数曲线的频率响应函数。通过逼近理论,可以用泰勒展开(多项式逼近函数去近似函数):
H = h 0 L 0 + h 1 L 1 + . . . + h K L K = ∑ k = 0 K h k L k H=h_0L^0+h_1L^1+...+h_KL^K=\sum_{k=0}^{K}h_kL^k H=h0L0+h1L1+...+hKLK=k=0∑KhkLk
其中K是图滤波器H的阶数。对于图滤波器可以从空域和频率两个角度理解。
5.4.1 空域角度
对于 y = H x = ∑ k = 0 K h k L k x \pmb y=H\pmb x=\sum_{k=0}^Kh_kL^k\pmb x yyy=Hxxx=∑k=0KhkLkxxx,可以设定
x ( k ) = L k x = L x ( k − 1 ) \pmb x^{(k)}=L^k\pmb x=L\pmb x^{(k-1)} xxx(k)=Lkxxx=Lxxx(k−1)
则
y = ∑ k = 0 K h k x ( k ) \pmb y=\sum_{k=0}^K\pmb h_k\pmb x^{(k)} yyy=k=0∑Khhhkxxx(k)
上述式子就将输出信号变成了(K+1)组图信号的线性加权,对于式(5.22),由于L是一个图位移算子,因此, x ( k − 1 ) x^{(k-1)} x(k−1)到 x ( k ) \pmb x^{(k)} xxx(k)的变换只需要所有节点的一阶邻居参与计算。
总的来看, x ( k ) \pmb x^{(k)} xxx(k)的计算只需要所有节点的k阶邻居参与。我们称这种性质为图滤波器的局部性。
从空域角度来看,滤波操作具有以下性质:
- 具有局部性,每个节点的输出信号值只需要考虑其K阶子图;
- 通过K步迭代式的矩阵向量乘法来完成滤波操作。
5.4.2 频域角度
由于 L = V Λ V T L=V\Lambda V^T L=VΛVT,则:
KaTeX parse error: Unknown column alignment: 0 at position 109: …[ \begin{array}0̲ \sum_{k=0}^Kh_…
通过上式,H的频率响应函数为 λ \lambda λ的K次代数多项式,如果K足够大,我们可以用这种形式去逼近任何一个关于 λ \lambda λ的函数:
y = H x = V ( ∑ k = 0 K h k Λ k ) V T x \pmb y=H\pmb x=V(\sum_{k=0}^Kh_k\Lambda^k)V^T\pmb x yyy=Hxxx=V(k=0∑KhkΛk)VTxxx
过程如下:
- 通过图傅里叶变换,使用 V T x V^T\pmb x VTxxx将图信号变换到频域空间;
- 通过 Λ h = ∑ k = 0 K h k Λ k \Lambda_h=\sum_{k=0}^Kh_k\Lambda^k Λh=∑k=0KhkΛk对频率分量的强度进行调节得到 y ~ \tilde {\pmb y} yyy~;
- 通过逆图傅里叶变换,将 V y ~ 反 解 成 图 信 号 y V\tilde{\pmb y}反解成图信号\pmb y Vyyy~反解成图信号yyy。
多项式系数 h k \pmb h_k hhhk构成向量 h \pmb h hhh,则H的频率响应矩阵为
KaTeX parse error: Unknown column alignment: 0 at position 99: …[ \begin{array}0̲ 1&\lambda_1&..…
可以反解得到多项式系数:
h = Ψ − 1 d i a g − 1 ( Λ h ) \pmb h=\Psi^{-1}diag^{-1}(\Lambda_h) hhh=Ψ−1diag−1(Λh)
d i a g − 1 diag^{-1} diag−1表示将对角矩阵变成列向量。
图滤波操作性质总结:
- 从频域视角能够更清晰地完成对图信号的特定滤波操作;
- 图滤波器如何设计具有显式的公式指导;
- 对矩阵特征分解非常耗时,时间复杂度 O ( N 3 ) O(N^3) O(N3),相比空域视角,工程上有局限。
5.5 图卷积神经网络
两组图信号 x 1 、 x 2 \pmb x_1、\pmb x_2 xxx1、xxx2,其图卷积运算如下:
x 1 ∗ x 2 = IGFT ( GFT ( x 1 ) ⊙ GFT ( x 2 ) ) \pmb x_1*\pmb x_2=\text{IGFT}(\text {GFT}(\pmb x_1)\odot \text{GFT}(\pmb x_2)) xxx1∗xxx2=IGFT(GFT(xxx1)⊙GFT(xxx2))
⊙ \odot ⊙表示哈达玛积。
与图信号处理中同理,时域中卷积等价于频域中乘法。
x 1 ∗ x 2 = V ( ( V T x 1 ) ⊙ ( V T x 2 ) ) = V ( x 1 ~ ⊙ ( V x 2 ) ) = V ( d i a g ( x 1 ~ ) ( V T x 2 ) ) = ( V ( d i a g ( x 1 ~ ) V T ) x 2 \pmb x_1*\pmb x_2=V((V^T\pmb x_1)\odot(V^T\pmb x_2))=V(\tilde {\pmb x_1}\odot(V\pmb x_2))\\ =V(diag(\tilde{\pmb x_1})(V^T\pmb x_2))\\ =(V(diag(\tilde{\pmb x_1})V^T)\pmb x_2 xxx1∗xxx2=V((VTxxx1)⊙(VTxxx2))=V(xxx1~⊙(Vxxx2))=V(diag(xxx1~)(VTxxx2))=(V(diag(xxx1~)VT)xxx2
令 H x 1 ~ = V d i a g ( x 1 ~ ) V T H_{\tilde{\pmb x_1}}=Vdiag(\tilde{\pmb x_1})V^T Hxxx1~=Vdiag(xxx1~)VT,显然H是一个图位移算子,其频率响应矩阵为 x 1 \pmb x_1 xxx1的频谱,于是可得到
x 1 ∗ x 2 = H x 1 ~ x 2 \pmb x_1*\pmb x_2=H_{\tilde{\pmb x_1}}\pmb x_2 xxx1∗xxx2=Hxxx1~xxx2
由上可知,两组图信号的图卷积运算总能转化为对应形式的图滤波运算,因此图卷积等价于图滤波。
可以拓展到多维图信号的,设矩阵 X ∈ R N × d X\in R^{N\times d} X∈RN×d,可以看作d组定义在G上的图信号,d为图信号的总通道数。例如 Y = H X Y=HX Y=HX,我们可以理解为图滤波器H对信号矩阵X每个通道的信号分别进行滤波操作。
三个工作:1.对频率相应矩阵进行参数化
KaTeX parse error: Unknown column alignment: 0 at position 35: …t[\begin{array}0̲ \theta_1\\ &\t…
上式的两种理解:
- 空域角度是引入了一个自适应的图位移算子,通过学习的手段指导该算子的学习,从而完成对输入图信号的针对性变换操作;
- 频域角度是该层在 X 与 X ′ X与X^{'} X与X′之间训练了一个可自适应的图滤波器,图滤波器的频率响应函数怎样,可以通过任务与数据之间的对应关系进行监督学习。
问题:引入学习参数过多,等于图中的节点数。
在真实图数据中,有效信息都隐藏在低频段,因此图滤波器设置N个维度的自由度。
三个工作:2.对多项式参数进行参数化
我们为了拟合任意的频率响应函数,可以将拉普拉斯矩阵的多项式形式转化为一种可学习的形式
X ′ = σ ( V ( ∑ k = 0 K θ k Λ k ) V T X ) = σ ( V d i a g ( Ψ θ ) V T X ) , Ψ 是 范 德 蒙 矩 阵 X^{'}=\sigma(V(\sum_{k=0}^K\theta_k\Lambda^k)V^TX)=\sigma(Vdiag(\Psi\theta)V^TX),\Psi是范德蒙矩阵 X′=σ(V(k=0∑KθkΛk)VTX)=σ(Vdiag(Ψθ)VTX),Ψ是范德蒙矩阵
学习参数 θ = [ θ 1 , . . . , θ K ] \theta=[\theta_1,...,\theta_K] θ=[θ1,...,θK],K可以控制,一般K远小于N。K越大,拟合的频率响应函数次数越高,可以拟合更复杂的滤波关系。
三个工作:3.设计固定的图滤波器
参数和矩阵特征分解给计算带来了困难,我们直接限制K=1:
X ′ = σ ( θ 0 X + θ 1 L X ) X^{'}=\sigma(\theta_0X+\theta_1LX) X′=σ(θ0X+θ1LX)
直接令 θ 0 = θ 1 = θ \theta_0=\theta_1=\theta θ0=θ1=θ,
X ′ = σ ( θ ( L + I ) X ) = σ ( θ L ~ X ) X^{'}=\sigma(\theta(L+I)X)=\sigma(\theta\tilde LX) X′=σ(θ(L+I)X)=σ(θL~X)
θ \theta θ是一个标量,相当于对 L ~ \tilde L L~的频率响应函数做了一个尺度变换,尺度变换可以再神经网络模型中被归一化操作替代。
因此可以设置 θ = 1 \theta=1 θ=1。
然后就有固定的图滤波器 L ~ \tilde L L~.
为了加强网络学习的稳定性,可以对 L ~ \tilde L L~做归一化处理。令 L ~ s y m = D ~ − 1 2 A ~ D ~ − 1 2 , A ~ = A + I , D ~ i i = ∑ j A ~ i j \tilde L_{sym}=\tilde D^{-\frac{1}{2}}\tilde A\tilde D^{-\frac{1}{2}},\tilde A=A+I,\tilde D_{ii}=\sum_{j}\tilde A_{ij} L~sym=D~−21A~D~−21,A~=A+I,D~ii=∑jA~ij, L ~ \tilde L L~被叫做重归一化形式的拉普拉斯矩阵,起特征值范围 ( − 1 , 1 ] (-1,1] (−1,1],可以防止多层网络优化时出现的梯度消失或爆炸。
增强网络拟合能力,增加参数权重矩阵W对输入图信号进行仿射变换
X ′ = σ ( L ~ s y m X W ) X^{'}=\sigma(\tilde L_{sym}XW) X′=σ(L~symXW)
这就是GCN layer(图卷积层),以此为基础堆叠的多层神经网络模型叫做图卷积模型。
图卷积层是对频率响应函数拟合形式上的极大简化。图滤波器退化为 L ~ s y m \tilde L_{sym} L~sym,图卷积操作变为 L ~ s y m X \tilde L_{sym}X L~symX。如果将X由信号矩阵切换到特征矩阵上,那么 L ~ s y m \tilde L_{sym} L~sym是一个图位移算子,根据矩阵乘法的行向量视角, L ~ s y m X \tilde L_{sym}X L~symX的计算等价于对邻居节点的特征向量进行聚合操作,于是又如下节点层面的公式:(这里的特征向量和特征矩阵理解不是很清楚,但 L ~ s y m \tilde L_{sym} L~sym作为图位移算子,相当于对邻居节点的聚合操作可以理解)
x i = σ ( ∑ v j ∈ N ( v i ) L ~ s y m [ i , j ] ( W x j ) ) \pmb x_i=\sigma(\sum_{v_j\in N(v_i)} \tilde L_{sym}[i,j](Wx_j)) xxxi=σ(vj∈N(vi)∑L~sym[i,j](Wxj))
L ~ s y m \tilde L_{sym} L~sym可以用稀疏矩阵表示。
实际任务中的有效性:
- L ~ s y m \tilde L_{sym} L~sym本身具有的滤波特性比较符号 真实数据的特有性质(章节6.3详细说明),能对数据实现高效滤波操作;
- 虽然GCN是对频率响应函数的线性近似推导出的,但是同其它深度网络模型一样,GCN堆叠多层时仍可以达到高阶多项式形式的频率响应函数的滤波能力。
两种模型:
- 频域卷积模型:进行矩阵特征分解从而进行图卷积计算的模型;
x_i=\sigma(\sum_{v_j\in N(v_i)} \tilde L_{sym}i,j)
$$
L ~ s y m \tilde L_{sym} L~sym可以用稀疏矩阵表示。
实际任务中的有效性:
- L ~ s y m \tilde L_{sym} L~sym本身具有的滤波特性比较符号 真实数据的特有性质(章节6.3详细说明),能对数据实现高效滤波操作;
- 虽然GCN是对频率响应函数的线性近似推导出的,但是同其它深度网络模型一样,GCN堆叠多层时仍可以达到高阶多项式形式的频率响应函数的滤波能力。
两种模型:
- 频域卷积模型:进行矩阵特征分解从而进行图卷积计算的模型;
- 空域卷积模型:不需要进行矩阵特征分解进行图卷积计算的模型,工程上具有优越性。