机器学习回归（regression）——线性回归（Hung-yi Lee）

前言

机器学习可简单分为监督学习和非监督学习。从下图也可以看出来，分类和回归属于监督学习，聚类和降维属于非监督学习。而回归又是大多数机器学习学习者最先接触的任务，本文主要讲述线性回归，作为一个学习笔记。

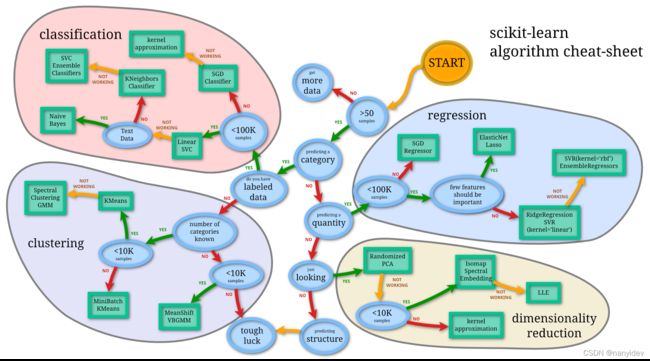
监督学习:
给定一组训练数据，通常是($x^1$,$y^1$),($x^2$,$y^2$),($x^3$,$y^3$)$\cdots$,其中y是标签，$x^m$=（$x_1^m$,$x_2^m$,$x_3^m$$\cdots$）是第m个数据对应的特征，通常是一个向量。
回归模型是有监督模型的一种，线性回归是回归模型的一种。线性表示f是关于x的线性函数；回归表示y是一个连续的标量值

回归三步走

Step1 define a set of function

基于训练数据定义一个预测函数(模型)
问题描述：（还是拿李老师的课件来讲吧）
预测一只pokemon进化后的CP值即y（combat power，战斗力），可能影响因素有进化前的CP值$x$_cp，属于物种类别$x_s$，生命值$x$_hp，体重$x_w$，身高$x_h$。
暂且只考虑$x$_cp，因为是线性回归，则可以假设y与$x$_cp之间的function是$$y=w\ast x_{cp}+b$$
其中w和b都是参数，则可能有
$f1：y=10.0\ast x_{cp}+9.0$
$f2：y=-0.8\ast x_{cp}-1.2$
等，即线性回归的一般函数是：$y=b+\sum w_i{x}_i$

Step2 goodness of function

评判选择函数（模型）的好坏，此时定义一个loss function$$L(w,b)=\sum _{n=1}^{10}({\hat{y}}^n-f(x_{cp}^n){)}^2$$ 其中$\hat{y}$是真实值，$f(x_{cp}^n)=w\ast x_{cp}^n+b$,loss的含义即每一项真实值与每一项预测值的差。

Step3 pick the best function

选择最好的模型，即最优化问题：
$f^{\ast }=arg\underset{f}{\min }L(w,b)$， $w^{\ast },b^{\ast }=arg\underset{w,b}{\min }L(w,b)$
先考虑优化一个参数（如w），则利用梯度下降的方法：

1.随机选取一个初值$w^0$
2. 计算此处的梯度值$\frac{dl}{dw}{|}_{w=w^0}$
3. 迭代更新参数，$w^1=w^0-\eta \ast \frac{dl}{dw}{|}_{w=w^0}$，即需要朝着梯度的方向前进，其中$\eta$也被称之为学习率（learning rate）
接下来一直更新参数，直到找到梯度为零的点。

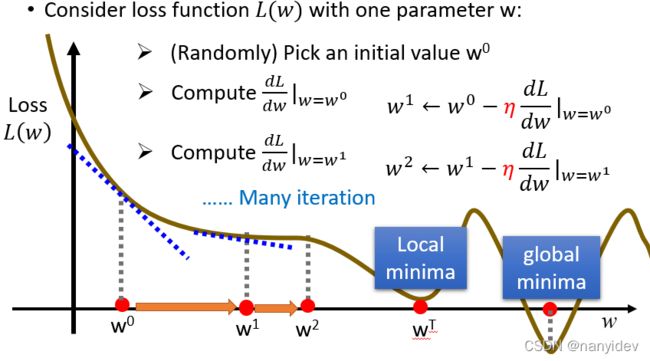
可以看到实际情况中可能存在局部最小点和全局最优点，所以梯度下降有可能不能找到全局最小点（梯度为0迭代就停止了），但就线性规划来说不用担心这个问题（线性规划的loss是凸函数）
如果是两个参数也是一样，$w^1=w^0-\eta \ast \frac{dl}{dw}{|}_{w=w^0,b=b^0}$，$b^1=b^0-\eta \ast \frac{dl}{db}{|}_{w=w^0,b=b^0}$。此时可以从看成一个平面某处走向最低点。

总结一下，线性规划就是利用梯度下降法找到合适的参数让loss函数最小，可以简写成
${\theta }^{\ast }=arg\underset{\theta }{\max }L(\theta )$，$\theta =(w,b,\cdots )$

实验结果分析

利用十组训练集得出结果（$y=b+w\ast x_{cp}$）
解得w=2.7,b=-188.4,此时训练集上的平均误差是31.9，测试集上的误差是35.0，显然误差较大，那怎么做才可以让误差更小呢——换函数（模型）

函数（模型）	训练集上的error	测试集上的error
$y=b+w\ast x_{cp}$	31.9	35.0
$y=b+w_1\ast x_{cp}+w_2\ast x_{cp}^2$	15.4	18.4
$y=b+w_1\ast x_{cp}+w_2\ast x_{cp}^2+w_3\ast x_{cp}^3$	15.3	18.1
$y=b+w_1\ast x_{cp}+w_2\ast x_{cp}^2+w_3\ast x_{cp}^3+w_4\ast x_{cp}^4+w_5\ast x_{cp}^5$	12.8	232.1

可以看出，随着模型越来越复杂，训练集误差一直再减小，但是测试集一开始在减小，之后却反而增大。此时模型产生了过拟合（overfitting）
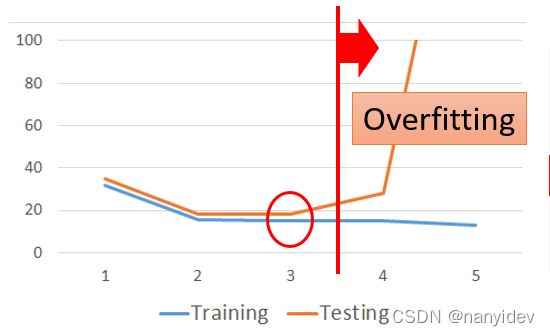也就是说：

A more complex model yields lower error on training data；
A more complex model does not always lead to better performance on testing data

解决过拟合的两种方式：
1.重新设计函数（模型）
可以考虑更多的因素，在一开始只考虑了进化前的CP值对进化后的CP值的影响，现在探索是不是还有其他因素，例如$x_{hp}$,$x_h$,$x_w$等，将这些因素也考虑进去。
2.在设计loss函数时，进行正则化
$$L(w,b)=\sum _n({\hat{y}}^n-(w_i\ast x_i^n+b){)}^2+\lambda \sum （w_i{)}^2$$
这可以让loss函数更平滑(smooth),这样可以让输出对于输入的变化不是那么敏感。