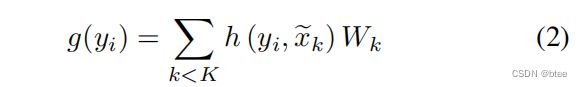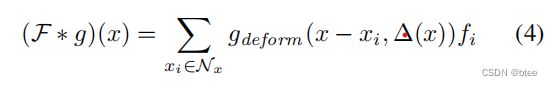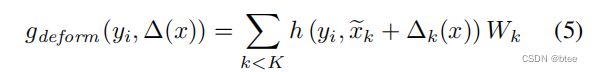论文翻译 | KPConv: Flexible and Deformable Convolution for Point Clouds

论文翻译：KPConv: Flexible and Deformable Convolution for Point Clouds

论文：KPConv: Flexible and Deformable Convolution for Point Clouds
代码地址：【here】

摘要

我们提出了一种核点卷积KPConv，一种新型的点卷积的方式，它可以在点云上工作而不需要任何的中间表示。KPConv这种卷积的权重通过核点来定位到欧几里得的空间，作用到离它们相近的点上。比起固定的卷积而言，它有更灵活用KPConv的任意核点的能力。不仅如此，这些定位是空间连续的，并且可以通过网络学习到。因此，KPConv可以被扩展到可形变的卷积，从而来学习去适应局部几何的核点。由于有着规则的下采样策略，KPConv也是对多种密度点高效并鲁棒的。不管它们在复杂任务上是否使用可形变的KPConv，或者在简单的任务上使用无形变的KPConv，我们的网络在一些分类或分割的数据上都比SOTA要好。我们也提供了消融实验，以及对KPConv学到了什么的理解，来证明可形变的KPConv是强大的且可解释的。

We present Kernel Point Convolution1(KPConv), a new design of point convolution, i.e. that operates on point clouds without any intermediate representation. The convolution weights of KPConv are located in Euclidean space by kernel points, and applied to the input points close to them. Its capacity to use any number of kernel points gives KPConv more flexibility than fixed grid convolutions. Furthermore, these locations are continuous in space and can be learned by the network. Therefore, KPConv can be extended to deformable convolutions that learn to adapt kernel points to local geometry. Thanks to a regular subsampling strategy, KPConv is also efficient and robust to varying densities. Whether they use deformable KPConv for complex tasks, or rigid KPconv for simpler tasks, our networks outperform state-of-the-art classification and segmentation approaches on several datasets. We also offer ablation studies and visualizations to provide understanding of what has been learned by KPConv and to validate the descriptive power of deformable KPConv.

引言

深度学习的曙光促使了以离散卷积作为基础模块的现代计算机视觉的发展。这种操作包括了在2D的网格上对邻域数据的融合。正由于它们是规则的结构，因此它们可以在现代硬件上高效的计算。但是，一旦失去这种规则的结构，卷积的操作就还没有被合适的定义好，使得它们能像在2D网格上一样高效。

The dawn of deep learning has boosted modern computer vision with discrete convolution as its fundamental building block. This operation combines the data of local neighborhoods on a 2D grid. Thanks to this regular structure, it can be computed with high efficiency on modern hardware, but when deprived of this regular structure, the convolution operation has yet to be defined properly, with the same efficiency as on 2D grids.

随着3D扫描技术的兴起，大量作用在不规则的数据上应用增多。比如，基于不规则点的3D点云分割或者是3D SLAM。点云是3D点或高维点的集合。在许多应用上，点还与相应的特征，比如颜色，结合起来了。在这个工作中，我们将点考虑成两个原色，3维点和D维特征。这样的点云的结构是很稀疏的，也是无序的。这和图像的网格结构很不一样。但是，它还是和网格有着相似之处的：它是空间意义上的，这对点卷积的构建很重要。在网格中，特征对定位到了对应矩阵的索引里，但在点云中，它们通过它们的点定位坐标。因此，点可以被看做结构化的元素，它的特征才是真实的数据。

Many applications relying on such irregular data have grown with the rise of 3D scanning technologies. For example, 3D point cloud segmentation or 3D simultaneous localization and mapping rely on non-grid structured data:
point clouds. A point cloud is a set of points in 3D (or higher-dimensional) space. In many applications, the points，are coupled with corresponding features like colors. In this work, we will always consider a point cloud as those two elements: the points P ∈ RN×3 and the features F ∈ RN×D. Such a point cloud is a sparse structure that has the property to be unordered, which makes it very different from a grid. However, it shares a common property with a grid which is essential to the definition of convolutions: it is spatially localized. In a grid, the features are localized by their index in a matrix, while in a point cloud, they are localized by their corresponding point coordinates. Thus, the points are to be considered as structural elements, and the features as the real data.

大量处理这种数据方法被提出来了，我们可以把它们分成不同的类别，我们只在相关的工作基础上进行发展。一些方法是基于网格的，它们的宗旨是将稀疏的3D数据映射到规整的结构中，这样卷积就可以更好的定义。其他的方法用MLP来直接处理点云

Various approaches have been proposed to handle such data, and can be grouped into different categories that we will develop in the related work section. Several methods fall into the grid-based category, whose principle is to project the sparse 3D data on a regular structure where a convolution operation can be defined more easily. Other approaches use multilayer perceptrons (MLP) to process point clouds directly, following the idea proposed by …

最近，出现了一些直接在点云上定义卷积的尝试。这些方法用到了空间意义性质来定义空间卷积。它们都有一个共同的思想就是，卷积应该定义一组局部应用于点云中的可定制的空间滤波器。

More recently, some attempts have been made to design a convolution that operates directly on points. These methods use the spatial localization property of a point cloud to define point convolutions with spatial kernels. They share the idea that a convolution should define a set of customizable spatial filters applied locally in the point cloud.

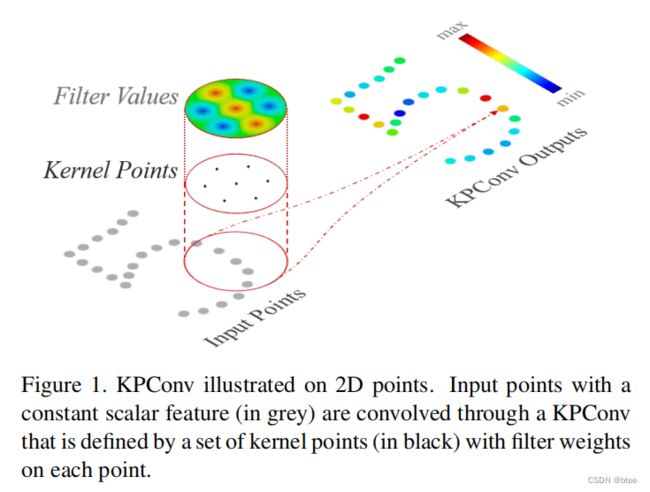
本文介绍了一种新的点卷积的方式KPConv。KPConv包括局部3D滤波器，同时也克服了以往工作中点卷积的局限性。KPConv灵感来自图像卷积，没有核的像素，取而代之的是一组核点来定义权重的应用位置，如图1所示。核点因此承载着核的权重，就像输入特征，它们的位置影响由相关运算定义。核点的数量是不限的，这样会很灵活。尽管很像词语，我们的工作不同之处在于，A的工作是来源于点云配准技术，核点没有权重分来学习局部几何形式。

This paper introduces a new point convolution operator named Kernel Point Convolution (KPConv). KPConv also consists of a set of local 3D filters, but overcomes previous point convolution limitations as shown in related work. KPConv is inspired by image-based convolution, but in place of kernel pixels, we use a set of kernel points to define the area where each kernel weight is applied, like shown in Figure 1. The kernel weights are thus carried by points, like the input features, and their area of influence is defined by a correlation function. The number of kernel points is not constrained, making our design very flexible. Despite the resemblance of vocabulary, our work differs from A ,which is inspired from point cloud registration techniques, and uses kernel points without any weights to learns local geometric patterns.

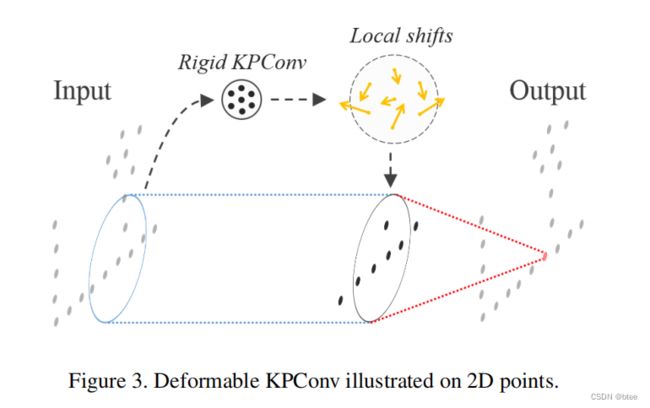
不仅如此，我们还提出了一种可形变的卷积版本，它包括了学习了核点的局部移动（如图3），我们的网络产生了每个卷积位置上的不同的移动，意味着，它可以适用不同输入点云领域的核的不同形状。我们的可形变卷积不是参照图像的。由于这种数据的不同性质，它需要一个正则化来帮这些形变了的卷积核适应点云几何特性，并且避免空的空间域。我们使用了有效感受野ERF并且加了消融实验来比较不可形变的卷积和可形变的卷积

Furthermore, we propose a deformable version of our convolution, which consists of learning local shifts applied to the kernel points (see Figure 3). Our network generates different shifts at each convolution location, meaning that it can adapt the shape of its kernels for different regions of the input cloud. Our deformable convolution is not designed the same way as its image counterpart. Due to the different nature of the data, it needs a regularization to help the deformed kernels fit the point cloud geometry and avoid empty space. We use Effective Receptive Field (ERF) [22] and ablation studies to compare rigid KPConv with deformable KPConv.

正如以往的文章所述，我们更偏向半径邻域而不是K近邻的邻域。一文章给出，KNN在不在规整的采样环境中，就不够鲁棒。我们卷积对不同密度的鲁棒性确保了点云的半径邻域和规整下采样。与规整化的策略相比，我们的方法避免了卷积的计算成本。

As opposed to [41, 2, 45, 20], we favor radius neighborhoods instead of k-nearest-neighbors (KNN). As shown by[13], KNN is not robust in non-uniform sampling settings. The robustness of our convolution to varying densities is ensured by the combination of radius neighborhoods and regular subsampling of the input cloud. Compared to normalization strategies, our approach also alleviates the computational cost of our convolution.

在我们的实验设置中，我们展示了KPConv可以面向分类或分割被用于构建非常深的架构，同时还能保持很快的训练和推理时间。总的来说，不可形变和可形变的KPConv都表现得很不错，在几个数据集的测试上都排在了前面。我们发现不可形变的KPConv 在简单的任务上表现得比较好，比如分类或小分割任务。可形变的在困难任务上胜出，一些大的分割任务，比如有很多物体或者更丰富的场景。我们也展示了可形变的 KPConv 在核点数小的时候会更鲁棒，这也暗示了更好的可解释性。最后，大量关于 KPConv ERF 的定性研究展示了可形变的核对适应场景物体的几何特性是有帮助的。

In our experiments section, we show that KPConv can be used to build very deep architectures for classification and segmentation, while keeping fast training and inference times. Overall, rigid and deformable KPConv both perform very well, topping competing algorithms on several datasets. We find that rigid KPConv achieves better performances on simpler tasks, like object classification, or
small segmentation datasets. Deformable KPConv thrives on more difficult tasks, like large segmentation datasets offering many object instances and greater diversity. We also
show that deformable KPConv is more robust to a lower number of kernel points, which implies a greater descriptive power. Last but not least, a qualitative study of KPConv ERF shows that deformable kernels improve the network ability to adapt to the geometry of the scene objects.

相关工作

在这一节中，我们简要的回顾了之前分析点云的深度学习的方法，也特别关注了和我们对点卷积定义相近的方法

In this section, we briefly review previous deep learning methods to analyze point clouds, paying particular attention to the methods closer to our definition of point convolutions.

投影网络：
一些方法将点投影到中间的网格结构上。基于图像的网格通常都是多视图的，用的是被点云作用到不同视图的2D图像。对于场景分割来说，这些方法会由于表面的遮挡和密度分布的不同而性能下降。除了选择全局的视图投影的方法，某方法也提出了将局部的邻域投影到一个局部切面上，然后用2D卷积处理它们。然而，这些方法都严重依赖于切线估计。

Projection networks. Several methods project points to an intermediate grid structure. Image-based networks are often multi-view, using a set of 2D images rendered from the point cloud at different viewpoints. For scene segmentation, these methods suffer from occluded surfaces and density variations. Instead of choosing a global projection viewpoint, [36] proposed projecting local neighborhoods to local tangent planes and processing them with 2D convolutions. However, this method relies heavily on tangent estimation.

在基于voxel的方法中，点被投影到3D的欧几里得的网格中。利用八叉树或者是哈希表这样的稀疏结构可以允许有更大的网格并且也能提升性能。但是，这些网络其实也缺少灵活性，因为它们的核都被限制成了3 33= 27 or 555 = 125 的网格。用多面体晶格替代欧几里得的网格可以把核减少到15个晶格，但是数量仍然是受限的，KPConv就允许任意数量的核点。不仅如此，在未来的工作中要避免中间结构，就应使架构更复杂如掩模的检测器或生成的模型更直接。

In the case of voxel-based methods, the points are projected on 3D grids in Euclidean space. Using sparse structures like octrees or hash-maps allows larger grids and enhanced performances, but these networks still lack flexibility as their kernels are constrained to use 3 33= 27 or 555 = 125 voxels. Using a permutohedral lattice instead of an Euclidean grid reduces the kernel to 15 lattices, but this number is still constrained, while KPConv allows any number of kernel points. Moreover, avoiding intermediate structures should make the design of more complex architectures like instance mask detector or generative models more straightforward in future works.

图卷积网络：
卷积的定义算子有不同的处理办法，图卷机可以被计算为谱表示上的乘法，或者它可以通过图被聚焦在表面。尽管图卷积和点卷积是很类似的，但是图卷积学习的是边缘关系的滤波器，而不是点之间的相对位置。换言之，图卷积聚合了一个局部区域表面的特征，但是对欧几里得空间中的变形是具有不变性的。相反，KPConv通过3D几何关系聚合了局部的信息，因此也捕获到了表面的形变

Graph convolution networks. The definition of a convolution operator on a graph has been addressed in different ways. A convolution on a graph can be computed as a multiplication on its spectral representation [8, 48], or it can focus on the surface represented by the graph [23, 5, 33, 25]. Despite the similarity between point convolutions and the most recent graph convolutions , the latter learn filters on edge relationships instead of points relative positions. In other words, a graph convolution combines features on local surface patches, while being invariant to the deformations of those patches in Euclidean space. In contrast, KPConv combines features locally according to the 3D geometry, thus capturing the deformations of the surfaces.

基于点的MLP网络：
PointNet 被看做是点云领域深度学习上的里程碑。这个网络在每个单独的点上都用了一个共享的MLP网络，然后做全局最大池化。这个共享的MLP网络作用是编码一系列学习到的空间信息，输入点云的全局描述被所有点的描述子的最大响应计算。这个网络的性能因为没有空间意义上的聚合信息而受限。在PointNet之后，一些继承的可以聚合局部信息的架构也被开发出来。

Pointwise MLP networks. PointNet is considered a milestone in point cloud deep learning. This network uses a shared MLP on every point individually followed by a global max-pooling. The shared MLP acts as a set of learned spatial encodings and the global signature of the input point cloud is computed as the maximal response among all the points for each of these encodings. The network’s performances are limited because it does not consider local spatial relationships in the data. Following PointNet, some hierarchical architectures have been developed to aggregate local neighborhood information with MLPs [27, 19, 21].

正如展示的那样，核点卷积也可以被MLP实现，因为它有能力，通过更复杂收敛更难的卷积的表示估计任何连续的函数。在我们的假设中，我们定义了一种像图像卷积一样显然的卷积核，不用MLP的中间表示。我们的设计也提供了直接的可变形版本，偏移量可以直接作用到核点上。

As shown by , the kernel of a point convolution can be implemented with a MLP, because of its ability to approximate any continuous function. However, using such a representation makes the convolution operator more complex and the convergence of the network harder. In our case, we define an explicit convolution kernel, like image convolutions, whose weights are directly learned, without the intermediate representation of a MLP. Our design also offers a straightforward deformable version, as offsets can directly be applied to kernel points.

点卷积网络
一些最近的工作经常定义点的卷积核，但KPConv通过它独有的设计脱颖而出。
Pointwise CNN将核的权重放在Voxel网格的箱体里，因此这样的做法并不灵活。此外，它们的归一化操作通常都让一些不必要的运算加重了网络的负荷，但是KPConv 的下采样策略就避免了密度不一和计算成本的问题。

Point convolution networks. Some very recent works also defined explicit convolution kernels for points, but KPConv stands out with unique design choices.
Pointwise CNN locates the kernel weights with voxel bins, and thus lacks flexibility like grid networks. Furthermore, their normalization strategy burdens their network with unnecessary computations, while KPConv subsampling strategy alleviates both varying densities and computational cost.

SpiderCNN将核定义为一组每个邻点有着不同权重的多项式函数。权重作用到邻点上是基于邻点的距离顺序。这就使滤波器在空间上不一致了。不同的是，KPConv 的权重是在空间上的，它使点的顺序具有不变性。

SpiderCNN defines its kernel as a family of polynomial functions applied with a different weight for each neighbor. The weight applied to a neighbor depends on the neighbor’s distance-wise order, making the filters spatially inconsistent. By contrast, KPConv weights are located in space and its result is invariant to point order.

Flex-convolution 对用了线性函数来对核建模，这就限制了核的表现形式。它同时用到的是KNN，如上述，KNN在不同密度的点云中不够鲁棒。

Flex-convolution uses linear functions to model its kernel, which could limit its representative power. It also uses KNN, which is not robust to varying densities as discussed above.

PCNN设计和KPConv很类似。它的定义也用到了点来承载核的权重和一个相关函数。然而，这样的设计不能扩展，因为它没有用到各种形式的邻点，它使卷积的计算和点的数目成二次关系，除此之外，它还用的高斯相关， KPConv 用到的是线性相关，线性相关在学习变形核的时候使梯度回传更有利。

PCNN design is the closest to KPConv. Its definition also uses points to carry kernel weights, and a correlation function. However, this design is not scalable because it does not use any form of neighborhood, making the convolution computations quadratic on the number of points. In addition, it uses a Gaussian correlation where KPConv uses a simpler linear correlation, which helps gradient backpropagation when learning deformations.

我们展示了KPConv比其他相关的网络都要好，并且据我们所知，没有以往的工作作了可形变的点卷积。

We show that KPConv networks outperform all comparable networks in the experiments section. Furthermore, to the best of our knowledge, none of the previous works experimented a spatially deformable point convolution.

核点卷积

3.1由点定义的核函数
正如之前的工作，在图像卷积的启发下，KPConv可以被一个总的点卷积的定义用公式表示出来。为了清晰可见，xi 表示三维点坐标，fi表示D维的点特征 ，被核g定义的卷积F 公式如下：

Like previous works, KPConv can be formulated with the general definition of a point convolution (Eq. 1), inspired by image convolutions. For the sake of clarity, we call xi and fi the points from P ∈ RN×3 and their corresponding features from F ∈ RN×D. The general point convolution of F by a kernel g at a point x ∈ R3 is defined as:

我们考虑了一篇论文给出的半径邻域的建议来确保不同密度的鲁棒性，因此Nx表示半径r之内的点，除此之外，一篇文章展示了手工3D描述子在半径邻域的条件下提供了比KNN更好的表示。我们相信，给一个给定一致的球形区域对核函数来学习到更有意义的表示是有帮助的。

We stand with [13] advising radius neighborhoods to ensure robustness to varying densities, therefore, Nx = xi ∈ P kxi xk 6 r with r ∈ R being the chosen radius. In addition, [38] showed that hand-crafted 3D point features offer a better representation when computed with radius neighborhoods than with KNN. We believe that having a consistent spherical domain for the function g helps the network to learn meaningful representations.

公式1中的重要的部分是核函数的定义，这就是 KPConv独特的地方之处。核函数g选择以X为中心的邻域位置为输入。我们把这个相对位置yi = xi-x叫yi。由于邻点是被半径定义的，核函数g 的定义域就是一个半径为r的闭球。和图像卷积类似，我们希望核函数对不同区域应用不同的权重。有很多方法来定义3维空间域，点是最直观的，特征都是定位到对应的点上。让落在闭球内的K个点作为核点，W为赋予这些核点的权重矩阵。使特征维 由Din变换到Dout。则半径为r的闭球内的核函数的定义为：

The crucial part in Eq. 1 is the definition of the kernel function g, which is where KPConv singularity lies. g takes the neighbors positions centered on x as input. We call them yi = xi-x in the following. As our neighborhoods are defined by a radius r, the domain of definition of g is the ball Br3 = y ∈ R3 | kyk 6 r. Like image convolution kernels (see Figure 2 for a detailed comparison between image convolution and KPConv), we want g to apply different weights to different areas inside this domain. There are many ways to define areas in 3D space, and points are the most intuitive as features are also localized by them. Let {exk | k < K} ⊂ B3r be the kernel points and {Wk | k < K} RDin×Dout be the associated weight matrices that map features from dimension Din to Dout. We define the kernel function g for any point yi ∈ Br3 as :

（我的看法，这里对核点的定义是为了让在不同相对位置上的点有着不同的权重，而这个权重可以由一个Wk线性表示。和图像不同，图像是整体学一个参数33DinDout,即可表示9DinDout，而这里的点卷积只学一个DinDout，再通过相对位置关系构造出其他K个不同位置不同维度的权重，这里的h好像只有一个维度，因此应该不能构造不同维度的权重）

这里h是xk和yi的相关函数，如果相近的话权重应该更高。h的公式为如下：σ表示距离的影响。与高斯相关相比较，线性相关会更简单。我们提倡这种更简单的相关性来简化梯度反向传播。利用校正线性单元Relu, 可以绘制并行图，这是深度神经网络中最流行的激活函数，由于其对梯度反向传播的效率。

where h is the correlation between xk and yi, that should be higher when exk is closer to yi. Inspired by the bilinear interpolation in [7], we use the linear correlation:

where σ is the influence distance of the kernel points, and will be chosen according to the input density (see Section 3.3). Compared to a gaussian correlation, which is used by [2], linear correlation is a simpler representation. We advocate this simpler correlation to ease gradient backpropagation when learning kernel deformations. A parallel can be drawn with rectified linear unit, which is the most popular activation function for deep neural networks, thanks to its
efficiency for gradient backpropagation.

不可形变或者可形变的核
核点的位置读卷积操作很关键。我们的不可形变的核需要被规则的排列才能有效率。当然我们说了KPConv的另一个强大的能力是它的灵活性。我们需要为任何一个K邻点找到一个规则的配置。我们选择了核点来解决这个优化问题，每个点对其他点都有一个斥力。但这些点又被相互之间的引力限制在一个球中，并且有个点还是中心点。我们在补充材料中详细说明了这部分。最终，周围的点被重新调整到平均半径为1.5σ，确保每个核点影响区域之间的小重叠和良好的空间覆盖

Kernel point positions are critical to the convolution operator. Our rigid kernels in particular need to be arranged regularly to be efficient. As we claimed that one of the KPConv strengths is its flexibility, we need to find a regular disposition for any K. We chose to place the kernel points by solving an optimization problem where each point applies a repulsive force on the others. The points are constrained to stay in the sphere with an attractive force, and one of them is constrained to be at the center. We detail this process and show some regular dispositions in the supplementary material. Eventually, the surrounding points are rescaled to an average radius of 1.5σ, ensuring a small overlap between each kernel point area of influence and a good space coverage.

对核有着合适的初始化之后，不可形变的 KPConv就已经很高效了，特别是给了一个足够大的K来覆盖g的球面域时。然而，还是可以通过学习位置的方式增强它的能力。核函数对每个核点来说是可微的，这说明可以有可学习的参数。我们可以考虑为每个卷积层学习一个全局的集合，但它不会比一个固定的规则配置带来更多的描述能力。反，网络为每个卷积位置x∈R3生成一组K位移∆(x)，并将可变形的KPConv定义为：

With properly initialized kernels, the rigid version of KPConv is extremely efficient, in particular when given a large enough K to cover the spherical domain of g. However it is possible to increase its capacity by learning the kernel point positions. The kernel function g is indeed differentiable with respect to exk, which means they are learnable parameters. We could consider learning one global set of {exk} for each convolution layer, but it would not bring more descriptive power than a fixed regular disposition. Instead the network generates a set of K shifts ∆(x) for every convolution location x ∈ R3 like [7] and define deformable KPConv as:

我们定义了一个offsets ∆k(x) 作为不可形变的KPConv的输出，如图3所示，通过训练网络能学到不可形变核，于是同时产生一个可形变的核，但是学不可形变核是学习率是0.1.
We define the offsets ∆k(x) as the output of a rigid KPConv mapping Din input features to 3K values, as shown in Figure 3. During training, the network learns the rigid kernel generating the shifts and the deformable kernel generating the output features simultaneously, but the learning rate of the first one is set to 0.1 times the global network learning rate.

遗憾的是，这种对图像可变形卷积的直接适应并不适合点云。在实践中，内核点最终被拉出输入点。于是这些核点被网络丢失了，因为当没有邻点时，它们的位移梯度∆k(x)是空的。关于这些“丢失了”的内核点的更多细节在补充部分中给出。为了解决这种行为，我们提出了一种“拟合”正则化损失，它惩罚核点与其输入邻居之间最近邻居之间的距离。此外，当所有对离核点的影响区域重叠时，我们还在它们之间增加了一个“排斥性”正则化损失，从而使它们不会重叠在一起。总的来说，我们对所有卷积位置x∈R3的正则化损失是：

Unfortunately, this straightforward adaptation of image deformable convolutions does not fit point clouds. In practice, the kernel points end up being pulled away from the input points. These kernel points are lost by the network, because the gradients of their shifts ∆k(x) are null when no neighbors are in their influence range. More details on these “lost” kernel points are given in the supplementary. To tackle this behaviour, we propose a “fitting” regularization loss which penalizes the distance between a kernel point and its closest neighbor among the input neighbors. In addition, we also add a “repulsive” regularization loss between all pair off kernel points when their influence area overlap, so that they do not collapse together. As a whole our regularization loss for all convolution locations x ∈ R3 is:
有了这种损失，网络就会生成符合输入点云的局部几何形状的位移。我们在补充材料中展示了这种效应。
With this loss, the network generates shifts that fit the local geometry of the input point cloud. We show this effect in the supplementary material.

核点网络层
通过下采样处理不同密度
正如介绍里说，我们通过下采样 来控制每一层的密度。为了确保点的采样位置的空间一致性，我们更倾向于不可形变的采样。因此，每一层的支撑包含了位置特征点，被选择为所有非空网格单元原始输入点的重心。

Subsampling to deal with varying densities. As explained in the introduction, we use a subsampling strategy to control the density of input points at each layer. To ensure a spatial consistency of the point sampling locations, we favor grid subsampling. Thus, the support points of each layer, carrying the features locations, are chosen as barycenters of theoriginal input points contained in all non-empty grid cells.

池化层
为了让架构有更多层，我们需要逐渐减少点的数量。我们已经网格降采样了，我们将每一个池化层的单元的尺寸加倍，并且有更多其他 的参数，并逐步增加点的感受野。被新位置上被池化过的点还可以被池化，我们用框架的后者并把它称为strided KPConv，和图像的步进卷积类比。

Pooling layer. To create architectures with multiple layer scales, we need to reduce the number of points progressively. As we already have a grid subsampling, we double the cell size at every pooling layer, along with the other related parameters, incrementally increasing the receptive
field of KPConv. The features pooled at each new location can either be obtained by a max-pooling or a KPConv. We use the latter in our architectures and call it “strided KPConv”, by analogy to the image strided convolution.

KPconv层
我们将3维点和对应的特征，以及对应的邻点矩阵作为输入。N0是邻点被计算的位置，和N不同。邻点矩阵被强制有个最大的 nmax邻点，因为大多数的邻点数都达不到 nmax，于是矩阵N就包含了一些没有用的元素。我们称它们为阴影邻居，在卷积计算过程中它们被忽略。

KPConv layer. Our convolution layer takes as input the points P ∈ RN×3 , their corresponding features F ∈ RN×Din , and the matrix of neighborhood indices N ∈[[1, N]]N0×nmax. N0 is the number of locations where the neighborhoods are computed, which can be different from N (in the case of “strided” KPConv). The neighborhood matrix is forced to have the size of the biggest neighborhood nmax. Because most of the neighborhoods comprise less than nmax neighbors, the matrix N thus contains unused elements. We call them shadow neighbors, and they are ignored during the convolution computations.

网络参数
每一层j都有一个单元格大小的dlj，我们从中可以推断出其他参数。核点的影响距离设置为 σj = Σ × dlj ，在不可形变的KPConv，给定平均核点半径为1.5σj，卷积半径自动设置为2.5σj。对于可变形的KPConv，卷积半径可以选择为rj=ρ×dlj。Σ和ρ是整个网络的比例系数集。除非另有说明，我们将对所有实验使用以下选择的参数集：K=15，Σ=1.0和ρ=5.0。第一个子采样单元格大小dl0将取决于数据集，如上所述，dlj+1=2∗dlj。

Network parameters. Each layer j has a cell size dlj from which we infer other parameters. The kernel points influence distance is set as equal to σj = Σ × dlj . For rigid KPConv, the convolution radius is automatically set to 2.5 σj given that the average kernel point radius is 1.5 σj . For deformable KPConv, the convolution radius can be chosen as rj = ρ × dlj . Σ and ρ are proportional coefficients set for the whole network. Unless stated otherwise, we will use the following set of parameters, chosen by cross validation, for all experiments: K = 15, Σ = 1.0 and ρ = 5.0. The first subsampling cell size dl0 will depend on the dataset and, as stated above, dlj+1 = 2 ∗ dlj .

核点卷积架构
结合成功的图像网络和实证研究，我们设计了两种网络体系结构的分类和分割任务。详细说明这两种体系结构的图表可在补充材料中找到。

Combining analogy with successful image networks and empirical studies, we designed two network architectures for the classification and the segmentation tasks. Diagrams detailing both architectures are available in the supplementary material.

KP-CNN是个5层的分类卷积网络。每层包含了2个卷积模块，除了第一层的每层的第一个卷积都进行的步进。我们的卷积块被设计得像bottleneck ResNet blocks ，用KPConv替换图像卷积、批处理归一化和leaky ReLu 激活。在最后一层之后，通过全局平均池化聚合，并且加上一个全连接和softmax。对于具有可变形的KPConv的结果，我们只在最后5个KPConv块中使用可变形的内核（参见补充材料中的体系结构细节）。

KP-CNN is a 5-layer classification convolutional network. Each layer contains two convolutional blocks, the first one being strided except for the first layer. Our convolutional blocks are designed like bottleneck ResNet blocks [12] with a KPConv replacing the image convolution, batch normalization and leaky ReLu activation. After the last layer, the features are aggregated by a global average pooling and processed by the fully connected and softmax layers like in an image CNN. For the results with deformable KPConv, we only use deformable kernels in the last 5 KPConv blocks
(see architecture details in the supplementary material).

KP-FCNN是个完全的分割卷积网络。编码器部分与KP-CNN中的相同，解码器部分使用最近的上采样来得到最终的点态特征。跳跃连接用于在编码器和解码器的中间层之间传递特征。这些特征被连接到上采样的特征上，并通过一元卷积进行处理，这相当于图像中的1×1卷积或点网中的共享MLP。可以用KPConv替换最近的上采样操作，这与扭曲的KPConv相同，但它不会导致性能的显著改进。

KP-FCNN is a fully convolutional network for segmentation. The encoder part is the same as in KP-CNN, and the decoder part uses nearest upsampling to get the final pointwise features. Skip links are used to pass the features between intermediate layers of the encoder and the decoder.
Those features are concatenated to the upsampled ones and processed by a unary convolution, which is the equivalent of a 1×1 convolution in image or a shared MLP in PointNet. It is possible to replace the nearest upsampling operation by a KPConv, in the same way as the strided KPConv, but it does not lead to a significant improvement of the performances.

实验

三维形状的分类和分割
我们在两个公开数据集上评估了我们的网络。我们用 ModelNet40作分类数据集，用ShapenetPart作分割的数据集。ModelNet40 包括了40个类别的12,311个

这里是引用

CAD模型，ShapenetPart是一个来自16个类别的16,681 的点云集合，每个点云有2-6个部分标签。为了一个基准的目标，我们用某篇论文提供的数据。在两种情况下，我们都遵循 train/test 的分割并且将物体重新放缩到一个单元球里（并在本实验的其余部分中考虑单位为米）。我们忽略了normals，因为它们只可用于人工数据。

Data. First, we evaluate our networks on two common model datasets. We use ModelNet40 [44] for classification and ShapenetPart for part segmentation. ModelNet40 contains 12,311 meshed CAD models from 40 categories. ShapenetPart is a collection of 16,681 point clouds from 16 categories, each with 2-6 part labels. For benchmarking purpose, we use data provided by [27]. In both cases, we follow standard train/test splits and rescale objects to fit them into a unit sphere (and consider units to be meters for the rest of this experiment). We ignore normals because they are only available for artificial data.

分类任务
我们首先设置了下采样的网格尺寸为 2cm。我们不加人任何特征作输入，每个输入点被分配一个等于1的常数特征，而不是可以被看成0的空空间。这个常数特征编码了输入点的集合信息，我们的增强过程包括缩放、翻转和扰动点。在设置中，我们在Nvidia Titan Xp上能做到每秒处理2.9个batch的16个点云。因为我们的下采样策略，输入点并没有保持一直相同的数量，我们的网络能接受不同的点云尺寸因此这也不是一个问题，平均而言，我们的框架中的ModelNet40 的物体点云包含了 6,800 点。其他参数和架构细节在补充材料中详细说明，并且还包括了参数量和训练和推理速度。

Classification task. We set the first subsampling grid size to dl0 = 2cm. We do not add any feature as input; each input point is assigned a constant feature equal to 1, as opposed to empty space which can be considered as 0. This constant feature encodes the geometry of the input points.
Like [2], our augmentation procedure consists of scaling, flipping and perturbing the points. In this setup, we are able to process 2.9 batches of 16 clouds per second on an Nvidia Titan Xp. Because of our subsampling strategy, the input point clouds do not all have the same number of points,
which is not a problem as our networks accept variable input point cloud size. On average, a ModelNet40 object point cloud comprises 6,800 points in our framework. The other parameters are detailed in the supplementary material, along with the architecture details. We also include the number of parameters and the training/inference speeds for both rigid and deformable KPConv.

如表1所示，我们的网络仅使用点就优于其他最先进的方法（我们没有考虑使用 normals作为额外输入的方法）。我们还注意到，不可形变的KPConv性能会稍好一些。我们猜测它可以用任务的简单性来解释。如果可变形的内核增加了更多的描述能力，也增加了整体网络的复杂性，这可能会干扰收敛或导致等简单任务的过拟合

As shown on Table 1, our networks outperform other state-of-the-art methods using only points (we do not take into account methods using normals as additional input). We also notice that rigid KPConv performances are slightlybetter. We suspect that it can be explained by the task simplicity. If deformable kernels add more descriptive power,they also increase the overall network complexity, which can disturb the convergence or lead to overfitting on simpler tasks like this shape classification.

分割任务
对于这个任务，我们使用与分类任务中具有相同参数的KP-FCNN体系结构，将位置(x，y，z)作为附加特征添加到常数1之后，并使用相同的增强过程。我们训练一个具有多个头的单一网络来分割每个对象类的各个部分。点云更小（平均2300个点），我们每秒可以处理4.1批16个形状。表1显示了实例平均值和类平均mIoU。我们在补充材料中详细说明了每个类的mIoU。KP-FCNN算法优于所有其他算法，包括那些使用图像或normals等附加输入的算法。形状分割是一个比形状分类更困难的任务，我们可以看到KPConv在可变形核下具有更好的性能。

Segmentation task. For this task, we use KP-FCNN architecture with the same parameters as in the classification task, adding the positions (x, y, z) as additional features to the constant 1, and using the same augmentation procedure. We train a single network with multiple heads to segment the parts of each object class. The clouds are smaller (2,300 points on average), and we can process 4.1 batches of 16 shapes per second. Table 1 shows the instance average, and the class average mIoU. We detail each class mIoU in the supplementary material. KP-FCNN outperforms all other algorithms, including those using additional inputs like images or normals. Shape segmentation is a more difficult task than shape classification, and we see that KPConv has better performances with deformable kernels.

3D场景分类
我们的第二个实验展示了我们的分割架构如何推广到真实的室内和室外数据。为此，我们选择在4个不同性质的数据集上测试我们的网络。Scannet，用于室内杂乱的场景，S3DIS，用于室内大空间，Semantic3D，用于户外固定扫描，和 Paris-Lille-3D，用于户外移动扫描。Scannet包含1513个小的训练场景和100个在线基准测试场景，这些被标注到了20个语义类。S3DIS涵盖了来自3个不同建筑的6个大型室内区域，共计2.73亿人，共标注了13个类。和[37]一样，我们提倡使用Area-5作为测试场景，以更好地衡量我们的方法的泛化能力。Semantic3D是一个在线基准，包括几个固定的激光雷达扫描不同的户外场景。在这个数据集中，超过40亿个点被8个类注释，但它们主要覆盖地面、建筑或植被，而且对象实例比其他数据集中更少。我们倾向reduced-8 challenge（作测试集） ，因为它对靠近扫描仪的物体的偏移较小。 Paris-Lille-3D 包含了4个不同城市超过2公里的街道，也是一个在线基准。该数据集的1.6亿个点用10个语义类进行了标注。

4.2. 3D Scene Segmentation
Data. Our second experiment shows how our segmentation architecture generalizes to real indoor and outdoor data. To this end, we chose to test our network on 4 datasets of different natures. Scannet [6], for indoor cluttered scenes, S3DIS [1], for indoor large spaces, Semantic3D [11], for outdoor fixed scans, and Paris-Lille-3D [31], for outdoor mobile scans. Scannet contains 1,513 small training scenes and 100 test scenes for online benchmarking, all annotated with 20 semantic classes. S3DIS covers six large-scale indoor areas from three different buildings for a total of 273 million points annotated with 13 classes. Like [37], we advocate the use of Area-5 as test scene to better measure the generalization ability of our method. Semantic3D is an online benchmark comprising several fixed lidar scans of different outdoor scenes. More than 4 billion points are annotated with 8 classes in this dataset, but they mostly cover ground, building or vegetation and there are fewer object instances than in the other datasets. We favor the reduced-8 challenge because it is less biased by the objects close to the scanner. Paris-Lille-3D contains more than 2km of streets in 4 different cities and is also an online benchmark. The 160 million points of this dataset are annotated with 10 semantic classes.

真实场景分割的流程
这些数据集中的三维场景太大了，不能作为一个整体进行分割。我们的KP-FCNN架构用于分割包含在球体中的小子云。在训练中，这些球体是在场景中随机挑选出来的。在测试中，我们定期在点云中选择球体，但确保每个点被不同的球体位置多次测试。与在模型数据集上的投票方案一样，每个点的预测概率被平均。当数据集被着色时，我们使用这三个颜色通道作为特征。我们仍然保持常数1特征，以确保黑/深的点不被忽略。对于我们的卷积，一个所有特征都等于零的点等于空空间。输入球面半径选择为50×dl0（根据模型40实验）。

Pipeline for real scene segmentation. The 3D scenes in these datasets are too big to be segmented as a whole. Our KP-FCNN architecture is used to segment small subclouds contained in spheres. At training, the spheres are picked randomly in the scenes. At testing, we pick spheres regularly in the point clouds but ensure each point is tested multiple times by different sphere locations. As in a voting scheme on model datasets, the predicted probabilities for each point are averaged. When datasets are colorized, we use the three color channels as features. We still keep the constant 1 feature to ensure black/dark points are not ignored. To our convolution, a point with all features equal to zero is equivalent to empty space. The input sphere radius is chosen as 50 × dl0 (in accordance to Modelnet40 experiment).

结果：由于室外对象比室内对象大，我们在Semantic3D 数据集和 Paris-Lille-3D上使用dl0=6cm，在Scannet和S3DIS上使用dl0=4cm。如表2所示，我们的架构在Scannet上排名第二，在其他数据集上优于所有其他分割架构。与其他点卷积架构相比，KPConv的性能超过了Scannet上的19个mIoU点，以及S3DIS上的9个mIoU点。而他们最初的论文中没有展示SubSparseCNN在Scannet 数据集上的得分，所以在不知道他们的实验设置的情况下很难进行比较。我们可以注意到，在相同的 ShapeNetPart 分割实验设置中，KPConv比SubSparseCNN多出近2个mIoU点。
在这4个数据集中，KPConv可变形核改进了Paris-Lille-3D和S3DIS上的结果，而不可形变版本在Scannet和Semantic3D 上的结果更好。如果我们遵循我们的假设，我们就可以解释在这个数据集中缺乏多样性的Semantic3D得分较低的原因。事实上，尽管它包含了15个场景和40亿个点，但它包含了大部分的地面、建筑和植被点，以及一些真实的物体，如汽车或行人。虽然这不是包含了1500多个具有不同对象和形状的场景Scannet的情况，但我们的验证研究并没有反映在这个基准测试上的测试分数上。我们发现，可变形的KPConv在几个不同的验证集上优于其刚性对应物（见第4.3节）。这些结果表明，可变形KPConv的描述能力对大型和不同数据集上的网络是有用的。我们相信KPConv可以在更大的数据集上茁壮成长，因为它的内核结合了强大的描述能力（与其他更简单的表示相比，如[10]的线性内核）和强大的可学习性(像[20,41]这样的MLP卷积的权重学习更复杂)。在Semantic3D和S3DIS上的分割场景的说明如图4所示。在补充材料中提供了更多的结果可视化。

Results. Because outdoor objects are larger than indoor objects, we use dl0 = 6cm on Semantic3D and Paris-Lille-3D, and dl0 = 4cm on Scannet and S3DIS. As shown in Table 2, our architecture ranks second on Scannet and outperforms all other segmentation architectures on the other datasets. Compared to other point convolution architectures, KPConv performances exceed previous scores by 19 mIoU points on Scannet and 9 mIoU points on S3DIS. SubSparseCNN score on Scannet was not reported in their original paper, so it is hard to compare without knowing their experimental setup. We can notice that, in the same experimental setup on ShapeNetPart segmentation, KPConv outperformed SubSparseCNN by nearly 2 mIoU points.

Among these 4 datasets, KPConv deformable kernels improved the results on Paris-Lille-3D and S3DIS while the rigid version was better on Scannet and Semantic3D. If we follow our assumption, we can explain the lower scores on Semantic3D by the lack of diversity in this dataset. Indeed, despite comprising 15 scenes and 4 billion points, it contains a majority of ground, building and vegetation points and a few real objects like car or pedestrians. Although this is not the case of Scannet, which comprises more than 1,500 scenes with various objects and shapes, our validation studies are not reflected by the test scores on this benchmark. We found that the deformable KPConv outperformed its rigid counterpart on several different validation sets (see Section 4.3). As a conclusion, these results show that the descriptive power of deformable KPConv is useful to the network on large and diverse datasets. We believe KP Conv could thrive on larger datasets because its kernel combines a strong descriptive power (compared to other simpler representations, like the linear kernels of [10]), and great learnability (the weights of MLP convolutions like are more complex to learn). An illustration of segmented scenes on Semantic3D and S3DIS is shown in Figure 4. More results visualizations are provided in the supplementary material.

消融实验
我们进行了一项消融研究来支持我们的主张，即可变形的KPConv比刚性的KPConv具有更强的描述能力。这个想法是为了阻碍网络的能力，以揭示可变形核的真正潜力。我们使用Scannet数据集（与以前相同的参数）并使用官方验证集，因为测试集不能用于此类评估。如图5所示，当限制在4个核点时，可变形的KPConv只损失了1.5%的mIoU。在相同的配置中，不可形变KPConv损失了3.5%的mIoU。

We conduct an ablation study to support our claim that deformable KPConv has a stronger descriptive power than rigid KPConv. The idea is to impede the capabilities of the network, in order to reveal the real potential of deformable kernels. We use Scannet dataset (same parameters as before) and use the official validation set, because the test set cannot be used for such evaluations. As depicted in Figure 5, the deformable KPConv only loses 1.5% mIoU when restricted to 4 kernel points. In the same configuration, therigid KPConv loses 3.5% mIoU.

如第4.2节所述，我们也可以看到是可变形的KPConv比有15个内核点的不可形变KPConv性能好。虽然在测试集上不是这样，但我们尝试了不同的验证集，这证实了可变形KPConv的优越性能。这并不奇怪，因为我们在S3DIS上得到了相同的结果。可变形的KPConv似乎在室内数据集上表现好，因为而室内数据集比室外数据集提供了更多的多样性。为了理解原因，我们需要不看数字，看看KPConv的两个版本有效地学到了什么。

As stated in Section 4.2, we can also see that deformable KPConv performs better than rigid KPConv with 15 kernel points. Although it is not the case on the test set, we tried different validation sets that confirmed the superior performances of deformable KPConv. This is not surprising as we
obtained the same results on S3DIS. Deformable KPConv seem to thrive on indoor datasets, which offer more diversity than outdoor datasets. To understand why, we need to go beyond numbers and see what is effectively learned by the two versions of KPConv.

`学习到的特征和有效的感受野
为了更深入地理解KPConv，我们提供了关于学习机制的两个见解。
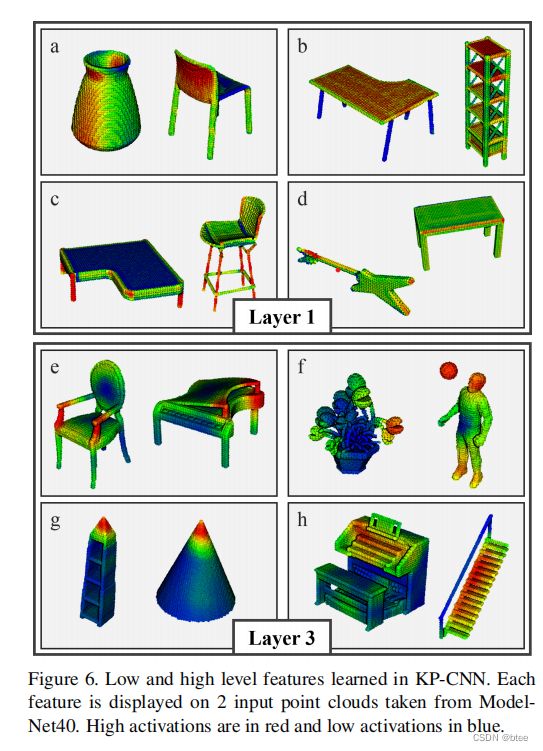
学习到的特征。我们的第一个想法是将我们的网络所学到的特征可视化。在这个实验中，我们用不可形变KPConv在ModelNet40上训练KP-CNN。我们围绕垂直轴增加了随机旋转增强，以增加输入形状的多样性。然后，我们通过根据这些特征的激活程度对点进行着色来可视化每个学习到的特征。在图6中，我们选择了输入点云，在第一层和第三层上最大化地激活不同的特征。为了获得更清晰的显示，我们将激活点从图层的下采样点投影到原始输入点。我们观察到，在它的第一层，网络能够学习低级的特征，如垂直/水平平面(a/b)，线性结构©，或角(d).在后面的几层中，该网络可以检测到更复杂的形状，如小扶壁(e)、球(f)、圆锥(g)或楼梯(h)。然而，很难看到不可形变和可变形的KPConv之间的区别。这个工具对于理解KPConv一般可以学习到什么非常有用，但我们需要另一个工具来比较这两个版本。

To achieve a deeper understanding of KPConv, we offer two insights of the learning mechanisms.
Learned features. Our first idea was to visualize the features learned by our network. In this experiment, we trained KP-CNN on ModelNet40 with rigid KPConv. We added random rotation augmentations around vertical axis to increase the input shape diversity. Then we visualize each learned feature by coloring the points according to their level of activation for this features. In Figure 6, we chose input point clouds maximizing the activation for different features at the first and third layer. For a cleaner display, we projected the activations from the layer subsampled points
to the original input points. We observe that, in its first layer, the network is able to learn low-level features like vertical/horizontal planes (a/b), linear structures ©, or corners (d). In the later layers, the network detects more complex shapes like small buttresses (e), balls (f), cones (g), or stairs (h). However, it is difficult to see a difference between rigid and deformable KPConv. This tool is very useful to understand what KPConv can learn in general, but we need another one to compare the two versions.

有效感受野

为了理解不可形变和可变形的KPConv学习到的表征之间的差异，我们可以计算其在不同位置的有效感受场(ERF)[22]。ERF是对每个输入点对特定位置的KPConv层结果的影响的度量。它被计算为在这个特定位置的KPConv响应相对于输入点特征的梯度。正如我们在图7中所看到的，ERF的变化取决于它所关注的对象。我们可以看到，不可形变的KPConvERF在每种类型的对象上都有一个相对一致的范围，而可变形的KPConvERF似乎是在适应对象的大小。的确，它覆盖了整张床，更集中在椅子和周围的地面上。当它以一个平面为中心时，它似乎也忽略了大部分平面，而是达到在场景中的更多细节。这种自适应行为表明，可变形的KPConv提高了网络对场景对象几何形状的适应能力，并解释了在室内数据集上更好的性能。

Effective Receptive Field. To apprehend the differences between the representations learned by rigid and deformable KPConv, we can compute its Effective Receptive Field (ERF) [22] at different locations. The ERF is a measure of the influence that each input point has on the result of a KPConv layer at a particular location. It is computed as the gradient of KPConv responses at this particular location with respect to the input point features. As we can see in Figure 7, the ERF varies depending on the object it is centered on. We see that rigid KPConv ERF has a relatively consistent range on every type of object, whereas deformable KPConv ERF seems to adapt to the object size. Indeed, it covers the whole bed, and concentrates more on the chair that on the surrounding ground. When centered on a flat surface, it also seems to ignore most of it and reach for further details in the scene. This adaptive behavior shows that deformable KPConv improves the network ability to adapt to the geometry of the scene objects, and explains the better performances on indoor datasets.

结论

在这项工作中，我们提出了KPConv，一个在点云上运行的卷积方法。KPConv以半径邻域作为输入，并使用一小组核点在空间上定位的权值来处理它们。我们定义了这个卷积算子的一个可变形版本，它学习局部位移，有效地变形卷积核，使它们适合点云几何。根据数据集的多样性，或所选择的网络配置，可变形和刚性的KPConv都是有价值的，我们的网络为几乎每个测试数据集带来了新的最先进的性能。我们发布了我们的源代码，希望能帮助进一步研究点云卷积架构。除了所提出的分类和分割网络之外，KPConv还可以用于cnn所解决的任何其他应用程序。我们相信，可变形的卷积可以在更大的数据集或具有挑战性的任务中蓬勃发展，如目标检测、激光雷达流计算，或点云完成。

In this work, we propose KPConv, a convolution that operates on point clouds. KPConv takes radius neighborhoods as input and processes them with weights spatially located by a small set of kernel points. We define a deformable version of this convolution operator that learns local shifts effectively deforming the convolution kernels to make them fit the point cloud geometry. Depending on the diversity of the datasets, or the chosen network configuration, deformable and rigid KPConv are both valuable, and our networks brought new state-of-the-art performances for nearly every tested dataset. We release our source code, hoping to help further research on point cloud convolutional architectures. Beyond the proposed classification and segmentation networks, KPConv can be used in any other application addressed by CNNs. We believe that deformable convolutions can thrive in larger datasets or challenging tasks such as object detection, lidar flow computation, or point cloud completion.