数字图像处理(一):图像分割
数字图像处理(一):图像分割
1 间断检测,以区域间灰度不连续性质进行的分割
三种基本类型的灰度级间断:点、线、边缘。
1.1 点检测
 ,
,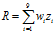
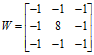
1.2 线检测
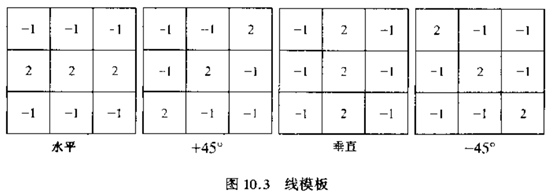
采用特定的模板可以检测出对应方向上的线条。
1.3 边缘检测
1.3.1 基本说明
边缘模型
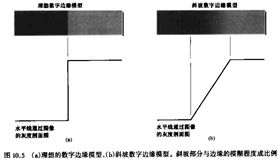
过渡段一阶导数为正,二阶导数为两个冲激信号。一阶导数确定某点是否是边缘点,二阶导数边缘两边像素的亮暗情况。导数对微弱噪声是极其敏感的。

1.3.2 梯度算子

表示f的最大变化率方向。向量的模: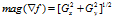 ;向量的方向:
;向量的方向: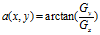 。
。
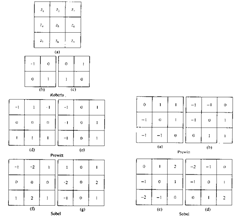
各种计算梯度的算子模板。
Roberts算子:没有明确的中心,不宜采用。
Prewitt算子:实现简单。
Sobel算子:抑制噪声性能好,平滑技术。并且对角线也可以很好的反应。
图10.8检测xy方向,图10.9检测对角线方向。
1.3.3 拉普拉斯算子
二维函数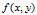 的拉普拉斯算子
的拉普拉斯算子
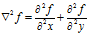
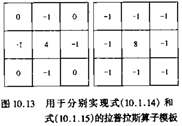
3*3模板
作用:(1)利用零交叉性质进行边缘定位(2)确定边缘两边的亮暗情况。
模糊函数:
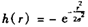
其实是一个高斯低通滤波器。然后求h的拉普拉斯算子,得到:
高斯型拉普拉斯算子LOG:又称墨西哥草帽函数
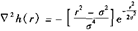 ,
,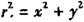
5*5的模板:

LOG的零交点处理:LOG图像二值化,过渡点就认为是零交点。但零交点是有很大不足的,梯度仍然是常用方法。
2 边缘连接和边缘检测
原因:由于噪声、不均匀的照明产生的边缘间断以及其他由于引入虚假的亮度间断的影响,一组像素无法完整描述一条边缘。
2.1 局部处理
确定边缘像素相似性:
(1)用于生成边缘像素的梯度算子的响应强度

(2)梯度向量的方向
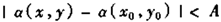
2.2 Hough变换
关键:点与线的对偶关系(一条直线可以在参数空间上表示为一个点)
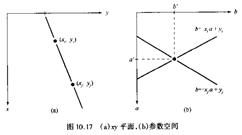
对偶关系说明:一条直线可由斜率和截距完全确定,也即 。而参数空间上的一条直线,表示几何空间上的一簇过定点
。而参数空间上的一条直线,表示几何空间上的一簇过定点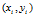 的直线。而参数空间上两条直线的交点确定了几何空间上的一条直线,并且这条直线既在过
的直线。而参数空间上两条直线的交点确定了几何空间上的一条直线,并且这条直线既在过 的直线集合,又在过
的直线集合,又在过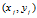 的直线集合,当然是一条由这两点确定的一条直线。
的直线集合,当然是一条由这两点确定的一条直线。
斜截式表示易于理解,但是无法表示过定点的所有直线。采用参数方程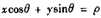 。几何表示:
。几何表示:
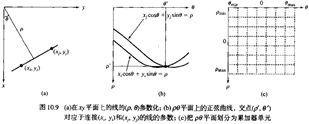
过一个定点的直线集合在参数平面上形成正弦曲线。

其中,有几条曲线在参数平面上通过一点就说明在几何平面上有几个点共线。上面的图是通过基于网格的累加器得到的。通过确定定点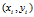 在每一个参数值
在每一个参数值 上得到对应的
上得到对应的 然后量化到网格中累加。利用HOUGH变换后,通过峰值检测得到可信度较高的直线;通过线段检测(始末点)和连接得到轮廓的叠加线段集合。
然后量化到网格中累加。利用HOUGH变换后,通过峰值检测得到可信度较高的直线;通过线段检测(始末点)和连接得到轮廓的叠加线段集合。
2.3 通过图论技术进行的全局处理
3 门限处理,以像素的分布性质进行的门限分割
3.1基础
操作函数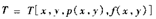 ,其中f表示点的灰度级,p表示点的局部特性。经过门限处理后
,其中f表示点的灰度级,p表示点的局部特性。经过门限处理后
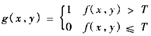
3.2 亮度的作用
图像模型:
 i亮度分量,r反射分量
i亮度分量,r反射分量
亮度条件不好就难以分割。
直方图的形成:反射函数和亮度函数的直方图卷积而成。
处理:采用补偿不均匀性的方法。
3.3 基本全局门限
迭代的方法:

3.4 基本自适应门限
通过将图像划分为子图,这些子图的直方图较为均匀。
3.5 最佳全局和自适应门限
基于概率密度函数,最大似然估计