相机标定（六）—— 张正友标定法

---

一、相机标定的目的

我们首先要明白两个问题：1、相机是如何成像的？2、相机标定的目的是什么？

1. 相机的成像过程

相机成像系统中，共包含四个坐标系：世界坐标系、相机坐标系、图像坐标系、像素坐标系。

这四个坐标系之间的转化关系为：

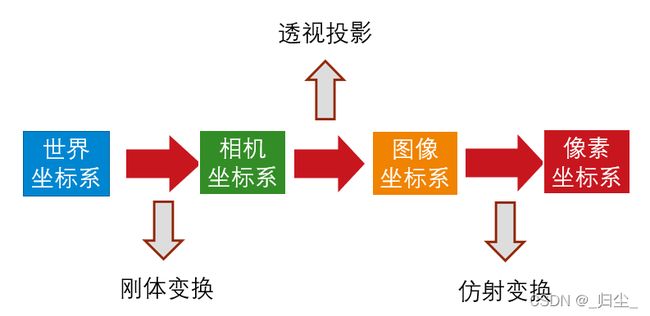
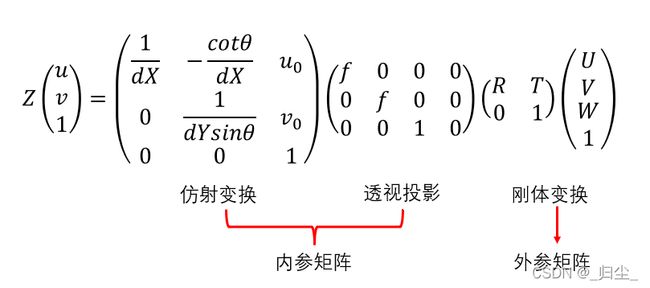
其中， $(U,V,W)$为在世界坐标系下一点的物理坐标， $(u,v)$为该点对应的在像素坐标系下的像素坐标， $Z$为尺度因子。

我们将矩阵：
$$\left(\begin{array}{ccc}\frac{1}{dX}& -\frac{cot\theta }{dX}& u_0\\ & & \\ 0& \frac{1}{dYsin\theta }& v_0\\ & & \\ 0& 0& 1\end{array}\right)\left(\begin{array}{cccc}f& 0& 0& 0\\ & & & \\ 0& f& 0& 0\\ & & & \\ 0& 0& 1& 0\end{array}\right)=\left(\begin{array}{cccc}\frac{f}{dX}& -\frac{fcot\theta }{dX}& u_0& 0\\ & & & \\ 0& \frac{f}{dYsin\theta }& v_0& 0\\ & & & \\ 0& 0& 1& 0\end{array}\right)$$
称为相机的内参矩阵，内参矩阵取决于相机的内部参数。其中，$f$为焦距，$dX,dY$分别表示$X,Y$方向上的一个像素在相机感光板上的物理长度（即一个像素在感光板上是多少毫米），$u_0,v_0$分别表示相机感光板中心在像素坐标系下的坐标，$\theta$表示感光板的横边和纵边之间的角度（90°表示无误差）。
我们将矩阵$\left(\begin{array}{cc}R& T\\ 0& 1\end{array}\right)$称为相机的外参矩阵，外参矩阵取决于相机坐标系和世界坐标系的相对位置，$R$表示旋转矩阵，$T$表示平移矢量。
即单点无畸变的相机成像模型如下：
$$Z\left(\begin{array}{c}u\\ \\ v\\ \\ 1\end{array}\right)=\left(\begin{array}{cccc}\frac{f}{dX}& -\frac{fcot\theta }{dX}& u_0& 0\\ & & & \\ 0& \frac{f}{dYsin\theta }& v_0& 0\\ & & & \\ 0& 0& 1& 0\end{array}\right)\left(\begin{array}{cc}R& T\\ & \\ 0& 1\end{array}\right)\left(\begin{array}{c}U\\ \\ V\\ \\ W\\ \\ 1\end{array}\right)$$

2. 相机标定的目的

为什么要进行相机标定呢？比如，当我们拿到一张图片，进行识别之后，得到的两部分之间的距离为多少像素，但是这多少像素究竟对应实际世界中的多少米呢？这就需要利用相机标定的结果来将像素坐标转换到物理坐标来计算距离（当然这里值得说明，仅仅利用单目相机标定的结果，是无法直接从像素坐标转化到物理坐标的，因为透视投影丢失了一个维度的坐标，所以测距其实需要双目相机）。

相机标定的目的其实很简单，我们要想对一个成像系统建模，进而进行相应的计算，所必须的参数就是相机的内参矩阵$\left(\begin{array}{cccc}\frac{f}{dX}& -\frac{fcot\theta }{dX}& u_0& 0\\ & & & \\ 0& \frac{f}{dYsin\theta }& v_0& 0\\ & & & \\ 0& 0& 1& 0\end{array}\right)$和相机的外参矩阵$\left(\begin{array}{cc}R& T\\ 0& 1\end{array}\right)$。因此，相机标定的第一个目的就是获得相机的内参矩阵和外参矩阵。

3. 畸变与畸变矫正

另外，相机拍摄的图片还存在一定的畸变，畸变包括桶形畸变和枕形畸变。
畸变模型包括径向畸变和切向畸变。
径向畸变公式（3阶）如下：
$$\begin{gathered} \hat{x}=x(1+k_1{r}^2+k_2{r}^4+k_3{r}^6) \\ \hat{y}=y(1+k_1{r}^2+k_2{r}^4+k_3{r}^6) \end{gathered}$$

切向畸变公式如下：
$$\begin{gathered} \hat{x}=x+(2p_{1}y+p_2(r^2+2x^2)) \\ \hat{y}=y+(p_1(r^2+2y^2)+2p_{2}x) \end{gathered}$$

其中，$(x,y),(\hat{x},\hat{y})$分别为理想的无畸变的归一化的图像坐标、畸变后的归一化图像坐标，$r$为图像像素点到图像中心点的距离，即$r^2=x^2+y^2$。

相机标定的第二个目的就是获得相机的畸变参数，如上式中的$k_1,k_2,k_3,p_1,p_2$等，进而对拍摄的图片进行去畸变处理。

二、张正友标定法简介

张正友标定法利用如下图所示的棋盘格标定板，在得到一张标定板的图像之后，可以利用相应的图像检测算法得到每一个角点的像素坐标$(u,v)$。

张正友标定法将世界坐标系固定于棋盘格上，则棋盘格上任一点的物理坐标$W=0$，由于标定板的世界坐标系是人为事先定义好的，标定板上每一个格子的大小是已知的，我们可以计算得到每一个角点在世界坐标系下的物理坐标$(U,V,W=0)$。

我们将利用这些信息：每一个角点的像素坐标$(u,v)$ 、每一个角点在世界坐标系下的物理坐标$(U,V,W=0)$，来进行相机的标定，获得相机的内外参矩阵、畸变参数。

三、标定相机内外参

张正友标定法标定相机的内外参数的思路如下：

1）、求解内参矩阵与外参矩阵的积；

2）、求解内参矩阵；

3）、求解外参矩阵。

1. 求解内参和外参的积

将世界坐标系固定于棋盘格上，则棋盘格上任一点的物理坐标$W=0$。因此，原单点无畸变的成像模型可以化为下式：
$$Z\left(\begin{array}{c}u\\ \\ v\\ \\ 1\end{array}\right)=\left(\begin{array}{ccc}\frac{f}{dX}& -\frac{fcot\theta }{dX}& u_0\\ & & \\ 0& \frac{f}{dYsin\theta }& v_0\\ & & \\ 0& 0& 1\end{array}\right)\left(\begin{array}{ccc}R1& R2& T\end{array}\right)\left(\begin{array}{c}U\\ \\ V\\ \\ 1\end{array}\right)=A\left(\begin{array}{ccc}R1& R2& T\end{array}\right)\left(\begin{array}{c}U\\ \\ V\\ \\ 1\end{array}\right)$$

其中，$R1,R2$为旋转矩阵$R$的前两列。为了简便，将内参矩阵记为$A$。

对于不同的图片，内参矩阵$A$为定值；对于同一张图片，内参矩阵$A$，外参矩阵$\left(\begin{array}{ccc}R1& R2& T\end{array}\right)$为定值；对于同一张图片上的单点，内参矩阵$A$，外参矩阵$\left(\begin{array}{ccc}R1& R2& T\end{array}\right)$，尺度因子$Z$为定值。

我们将$A\left(\begin{array}{ccc}R1& R2& T\end{array}\right)$记为矩阵$H$，$H$即为内参矩阵和外参矩阵的积，记矩阵$H$的三列为$\left(\begin{array}{ccc}H1& H2& H3\end{array}\right)$，则有：
$$\left(\begin{array}{c}u\\ v\\ 1\end{array}\right)=\frac{1}{Z}H\left(\begin{array}{c}U\\ V\\ 1\end{array}\right)=\frac{1}{Z}\left(\begin{array}{ccc}{H}_{11}& H_{12}& H_{13}\\ H_{12}& H_{22}& H_{32}\\ H_{31}& H_{32}& H_{33}\end{array}\right)\left(\begin{array}{c}U\\ V\\ 1\end{array}\right)$$
利用上式，消去尺度因子$Z$，可得：
$$\begin{gathered} u=\frac{H_{11}U+H_{12}V+H_{13}}{H_{31}U+H_{32}V+H_{33}} \\ v=\frac{H_{21}U+H_{22}V+H_{23}}{H_{31}U+H_{32}V+H_{33}} \end{gathered}$$

此时，尺度因子$Z$已经被消去，因此上式对于同一张图片上所有的角点均成立。$(u,v)$是像素坐标系下的标定板角点的坐标，$(U,V)$是世界坐标系下的标定板角点的坐标。通过图像识别算法，我们可以得到标定板角点的像素坐标$(u,v)$，又由于标定板的世界坐标系是人为定义好的，标定板上每一个格子的大小是已知的，我们可以计算得到世界坐标系下的$(U,V)$。

由这里的$H$是齐次矩阵，有8个独立未知元素。每一个标定板角点可以提供两个约束方程（$u,U,V$的对应关系，$v,U,V$的对应关系提供了两个约束方程）。因此，当一张图片上的标定板角点数量等于4时，即可求得该图片对应的矩阵H。当一张图片上的标定板角点数量大于4时，利用最小二乘法回归最佳的矩阵$H$。

2. 求解内参矩阵

我们已知了矩阵$H=A\left(\begin{array}{ccc}R1& R2& T\end{array}\right)$，接下来需要求解相机的内参矩阵$A$。

我们利用$R1,R2$作为旋转矩阵$R$的两列，存在单位正交的关系，即：
$$\begin{gathered} R{1}^{T}R2=0 \\ R{1}^{T}R1=R{2}^{T}R2=1 \end{gathered}$$
则由$H$和$R1,R2$的关系，可知：
$$\begin{gathered} R1=A^{-1}H1 \\ R2=A^{-1}H2 \end{gathered}$$
代入可得：
$$\begin{gathered} H{1}^T{A}^{-T}{A}^{-1}H2=0 \\ H{1}^T{A}^{-T}{A}^{-1}H1=H{2}^T{A}^{-T}{A}^{-1}H2=1 \end{gathered}$$

另外，我们发现，上述两个约束方程中均存在矩阵$A^{-T}{A}^{-1}$。因此，我们记$A^{-T}{A}^{-1}=B$，则$B$为对称阵。我们视图先求解出矩阵$B$，通过矩阵$B$再求解相机的内参矩阵$A$。

同时，为了简便，我们记相机内参矩阵$A$为：
$$A=\left(\begin{array}{cccc}\frac{f}{dX}& -\frac{fcot\theta }{dX}& u_0& 0\\ & & & \\ 0& \frac{f}{dYsin\theta }& v_0& 0\\ & & & \\ 0& 0& 1& 0\end{array}\right)=\left[\begin{array}{ccc}\alpha & \gamma & u_0\\ & & \\ 0& \beta & v_0\\ & & \\ 0& 0& 1\end{array}\right]$$

则：

$$A^{-1}=\left[\begin{array}{ccc}\frac{1}{\alpha }& -\frac{\gamma }{\alpha \beta }& \frac{\gamma v_0-\beta u_0}{\alpha \beta }\\ & & \\ 0& \frac{1}{\beta }& -\frac{v_0}{\beta }\\ & & \\ 0& 0& 1\end{array}\right]$$

则用矩阵$A$表示矩阵$B$得：
$$B=A^{-T}{A}^{-1}=\left[\begin{array}{ccc}\frac{1}{{\alpha }^2}& -\frac{\gamma }{{\alpha }^2\beta }& \frac{\gamma v_0-\beta u_0}{{\alpha }^2\beta }\\ & & \\ -\frac{\gamma }{{\alpha }^2\beta }& \frac{1}{{\beta }^2}+\frac{{\gamma }^2}{{\alpha }^2{\beta }^2}& \frac{\gamma (\beta u_0-\gamma v_0)}{{\alpha }^2{\beta }^2}-\frac{v_0}{{\beta }^2}\\ & & \\ \frac{\gamma v_0-\beta u_0}{{\alpha }^2\beta }& \frac{\gamma (\beta u_0-\gamma v_0)}{{\alpha }^2{\beta }^2}-\frac{v_0}{{\beta }^2}& \frac{(\beta u_0-\gamma v_0{)}^2}{{\alpha }^2{\beta }^2}+\frac{{v_0}^2}{{\beta }^2}+1\end{array}\right]=\left[\begin{array}{ccc}{B}_{11}& B_{12}& B_{13}\\ & & \\ B_{12}& B_{22}& B_{23}\\ & & \\ B_{13}& B_{23}& B_{33}\end{array}\right]$$

注意：由于$B$为对称阵，上式出现了两次$B_{12},B_{13},B_{23}$。

这里，我们可以使用$B=A^{-T}{A}^{-1}$将前面通过$R1,R2$单位正交得到的约束方程化为：
$$\begin{gathered} H{1}^{T}BH2=0 \\ H{1}^{T}BH1=H{2}^{T}BH2=1 \end{gathered}$$
因此，为了求解矩阵$B$，我们必须计算$H_i^{T}B{H}_j$。则：
$$\begin{gathered} H_i^{T}B{H}_j=\left[\begin{array}{ccc}{H}_{1i}& H_{2i}& H_{3i}\end{array}\right]\left[\begin{array}{ccc}{B}_{11}& B_{12}& B_{13}\\ & & \\ B_{12}& B_{22}& B_{23}\\ & & \\ B_{13}& B_{23}& B_{33}\end{array}\right]\left[\begin{array}{c}{H}_{1j}\\ \\ H_{2j}\\ \\ H_{3j}\end{array}\right] \\ =\left[\begin{array}{cccccc}{H}_{1i}{H}_{1j}& H_{1i}{H}_{2j}+H_{2i}{H}_{1j}& H_{2i}{H}_{2j}& H_{1i}{H}_{3j}+H_{3i}{H}_{1j}& H_{2i}{H}_{3j}+H_{3i}{H}_{2j}& H_{3i}{H}_{3j}\end{array}\right]\left[\begin{array}{c}{B}_{11}\\ \\ B_{12}\\ \\ B_{13}\\ \\ B_{22}\\ \\ B_{23}\\ \\ B_{33}\end{array}\right] \end{gathered}$$

上述方程看起来有点复杂，但是其实不然，我们可以记：
$$\begin{gathered} v_{ij}={\left[\begin{array}{cccccc}{H}_{1i}{H}_{1j}& H_{1i}{H}_{2j}+H_{2i}{H}_{1j}& H_{2i}{H}_{2j}& H_{1i}{H}_{3j}+H_{3i}{H}_{1j}& H_{2i}{H}_{3j}+H_{3i}{H}_{2j}& H_{3i}{H}_{3j}\end{array}\right]}^T \\ b={\left[\begin{array}{cccccc}{B}_{11}& B_{12}& B_{13}& B_{22}& B_{23}& B_{33}\end{array}\right]}^T \end{gathered}$$

则上述方程化为：
$$H_i^{T}B{H}_j=v_{ij}b$$

此时，通过$R1,R2$单位正交得到的约束方程可化为：
$$\begin{gathered} v_{12}^{T}b=0 \\ {v}_{11}^{T}b=v_{22}^{T}b=1 \end{gathered}$$

即：
$$\left[\begin{array}{c}{v}_{12}^T\\ \\ v_{11}^T-v_{22}^T\end{array}\right]b=vb=0$$
其中，矩阵$v=\left[\begin{array}{c}{v}_{12}^T\\ \\ v_{11}^T-v_{22}^T\end{array}\right]$

由于矩阵$H$已知，矩阵$v$又全部由矩阵$H$的元素构成，因此矩阵$v$已知。

此时，我们只要求解出向量$b$，即可得到矩阵$B$。每张标定板图片可以提供一个$vb=0$的约束关系，该约束关系含有两个约束方程。但是，向量$b$有6个未知元素。因此，单张图片提供的两个约束方程是不足以解出来向量$b$。因此，我们只要取3张标定板照片，得到3个$vb=0$的约束关系，即6个方程，即可求解向量$b$。当标定板图片的个数大于3时（事实上一般需要15到20张标定板图片），可采用最小二成拟合最佳的向量$b$，并得到矩阵$B$。
$$B=\left[\begin{array}{ccc}\frac{1}{{\alpha }^2}& -\frac{\gamma }{{\alpha }^2\beta }& \frac{\gamma v_0-\beta u_0}{{\alpha }^2\beta }\\ & & \\ -\frac{\gamma }{{\alpha }^2\beta }& \frac{1}{{\beta }^2}+\frac{{\gamma }^2}{{\alpha }^2{\beta }^2}& \frac{\gamma (\beta u_0-\gamma v_0)}{{\alpha }^2{\beta }^2}-\frac{v_0}{{\beta }^2}\\ & & \\ \frac{\gamma v_0-\beta u_0}{{\alpha }^2\beta }& \frac{\gamma (\beta u_0-\gamma v_0)}{{\alpha }^2{\beta }^2}-\frac{v_0}{{\beta }^2}& \frac{(\beta u_0-\gamma v_0{)}^2}{{\alpha }^2{\beta }^2}+\frac{{v_0}^2}{{\beta }^2}+1\end{array}\right]=\left[\begin{array}{ccc}{B}_{11}& B_{12}& B_{13}\\ & & \\ B_{12}& B_{22}& B_{23}\\ & & \\ B_{13}& B_{23}& B_{33}\end{array}\right]$$

根据矩阵$B$的元素和相机内参$\alpha ,\beta ,\gamma ,u_0,v_0$的对应关系（如上式），可得到：
$$\begin{gathered} v_0=\frac{B_{12}{B}_{13}-B_{11}{B}_{23}}{B_{11}{B}_{22}-B_{12}^2} \\ \alpha =\sqrt{\frac{1}{B_{11}}} \\ \beta =\sqrt{\frac{B_{11}}{B_{11}{B}_{22}-B_{12}^2}} \\ \gamma =-B_{12}{\alpha }^2\beta \\ {u}_0=\frac{\gamma v_0}{\beta }-B_{13}{\alpha }^2 \end{gathered}$$

即可求得相机的内参矩阵$A=\left(\begin{array}{cccc}\frac{f}{dX}& -\frac{fcot\theta }{dX}& u_0& 0\\ & & & \\ 0& \frac{f}{dYsin\theta }& v_0& 0\\ & & & \\ 0& 0& 1& 0\end{array}\right)=\left[\begin{array}{ccc}\alpha & \gamma & u_0\\ & & \\ 0& \beta & v_0\\ & & \\ 0& 0& 1\end{array}\right]$

3. 求解外参矩阵

这里再次强调一下，对于同一个相机，相机的内参矩阵取决于相机的内部参数，无论标定板和相机的位置关系是怎么样的，相机的内参矩阵不变。这也正是在第2部分“求解内参矩阵”中，我们可以利用不同的图片（标定板和相机位置关系不同）获取的矩阵$H$，共同求解相机内参矩阵$A$的原因。

但是，外参矩阵反映的是标定板和相机的位置关系。对于不同的图片，标定板和相机的位置关系已经改变，此时每一张图片对应的外参矩阵都是不同的。

在关系：$A\left(\begin{array}{ccc}R1& R2& T\end{array}\right)=H$中，我们已经求解得到了矩阵$H$（对于同一张图片相同，对于不同的图片不同）、矩阵$A$（对于不同的图片都相同）。通过公式：$\left(\begin{array}{ccc}R1& R2& T\end{array}\right)=A^{-1}H$，即可求得每一张图片对应的外参矩阵$\left(\begin{array}{ccc}R1& R2& T\end{array}\right)$。

注意，这里值得指出，完整的外参矩阵为$\left(\begin{array}{cc}R& T\\ 0& 1\end{array}\right)$。但是，由于张正友标定板将世界坐标系的原点选取在棋盘格上，则棋盘格上任一点的物理坐标$W=0$，将旋转矩阵的$R$的第三列$R3$消掉。因此，$R3$在坐标转化中并没有作用。但是$R3$要使得$R$满足旋转矩阵的性质，即列与列之间单位正交。因此可以通过向量$R1,R2$的叉乘，即$R3=R1\times R2$，计算得到$R3$。

此时，相机的内参矩阵和外参矩阵均已得到。

注：以上推导都是假设不存在畸变参数的情况下成立的。但是事实上，相机是存在畸变参数的，因此张正友标定法还需要通过L-M算法对于参数进行迭代优化。

四、标定相机的畸变参数

张正友标定法仅仅考虑了畸变模型中影响较大的径向畸变。

径向畸变公式（2阶）如下：
$$\begin{gathered} \hat{x}=x(1+k_1{r}^2+k_2{r}^4) \\ \hat{y}=y(1+k_1{r}^2+k_2{r}^4) \end{gathered}$$

其中，$(x,y),(\hat{x},\hat{y})$分别为理想的无畸变的归一化的图像坐标、畸变后的归一化图像坐标，$r$为图像像素点到图像中心点的距离，即$r^2=x^2+y^2$。

图像坐标和像素坐标的转化关系为：
$$\left(\begin{array}{c}u\\ v\\ 1\end{array}\right)=\left(\begin{array}{ccc}\frac{1}{dX}& -\frac{cot\theta }{dX}& u_0\\ & & \\ 0& \frac{1}{dYsin\theta }& v_0\\ & & \\ 0& 0& 1\end{array}\right)\left(\begin{array}{c}x\\ y\\ 1\end{array}\right)$$
其中，$(u,v)$为理想的无畸变的像素坐标。由于$\theta$接近于90°，则上式近似为：
$$\begin{gathered} u=\frac{x}{dX}+u_0 \\ v=\frac{y}{dY}+v_0 \end{gathered}$$
同理可得畸变后的像素坐标$(\hat{u},\hat{v})$的表达式为：
$$\begin{gathered} \hat{u}=\frac{\hat{x}}{dX}+u_0 \\ \hat{v}=\frac{\hat{y}}{dY}+v_0 \end{gathered}$$
代入径向畸变公式（2阶）则有：
$$\begin{gathered} \hat{u}-u_0=(u-u_0)(1+k_1{r}^2+k_2{r}^4) \\ \hat{v}-v_0=(v-v_0)(1+k_1{r}^2+k_2{r}^4) \end{gathered}$$
可化简得：
$$\begin{gathered} \hat{u}=u+(u-u_0)(k_1{r}^2+k_2{r}^4) \\ \hat{v}=v+(v-v_0)(k_1{r}^2+k_2{r}^4) \end{gathered}$$
即为：
$$\left[\begin{array}{cc}(u-u_0)r^2& (u-u_0)r^4\\ & \\ (v-v_0)r^2& (v-v_0)r^4\end{array}\right]\left[\begin{array}{c}{k}_1\\ \\ k_2\end{array}\right]=\left[\begin{array}{c}\hat{u}-u\\ \\ \hat{v}-v\end{array}\right]$$
每一个角点，只要知道畸变后的像素坐标$(\hat{u},\hat{v})$、理想的无畸变的像素坐标$(u,v)$，就可以构造两个上述等式。那么，有$m$幅图像，每幅图像上有$n$个标定板角点，则将得到的所有等式组合起来，可以得到$mn$个未知数为$k=[k_1,k_2{]}^T$的约束方程，将约束方程系数矩阵记为$D$，等式右端非齐次项记为$d$，可将其记为矩阵形式：
$$Dk=d$$
之后，利用最小二乘法可得：
$$k=\left[\begin{array}{c}{k}_1\\ \\ k_2\end{array}\right]=(D^{T}D{)}^{-1}{D}^{T}d$$
此时，相机畸变矫正参数已经标定好。

那么，如何获得畸变后的像素坐标$(\hat{u},\hat{v})$和理想的无畸变的像素坐标$(u,v)$呢？

$(\hat{u},\hat{v})$可以通过识别标定板的角点获得，$(u,v)$可以通过如下方法近似求得。世界坐标系下的每一个角点的坐标$(U,V)$是可以计算得到的，我们利用已经求得的外参矩阵$\left(\begin{array}{ccc}R1& R2& T\end{array}\right)$和内参矩阵$A$进行反投影。
$$Z\left(\begin{array}{c}u\\ \\ v\\ \\ 1\end{array}\right)=A\left(\begin{array}{ccc}R1& R2& T\end{array}\right)\left(\begin{array}{c}U\\ \\ V\\ \\ 1\end{array}\right)=H\left(\begin{array}{c}U\\ \\ V\\ \\ 1\end{array}\right)$$
利用上式，消去尺度因子$Z$，可得：
$$\begin{gathered} u=\frac{H_{11}U+H_{12}V+H_{13}}{H_{31}U+H_{32}V+H_{33}} \\ v=\frac{H_{21}U+H_{22}V+H_{23}}{H_{31}U+H_{32}V+H_{33}} \end{gathered}$$
即可得到理想的、无畸变的像素坐标$(u,v)$。当然，由于外参矩阵$\left(\begin{array}{ccc}R1& R2& T\end{array}\right)$和内参矩阵$A$是在有畸变的情况下获得的，这里得到的像素坐标$(u,v)$并不是完全理想的、无畸变的。我们的总逻辑是，在进行内参矩阵和外参矩阵的求解的时候，我们假设不存在畸变；在进行畸变系数的求解的时候，我们假设求得的内参矩阵和外参矩阵都是无误差的。最后，我们再通过L-M算法对于参数进行迭代优化。

需要指出，上述公式推导的时候以2阶径向畸变为例，但实际上更高阶的径向畸变同理，只是需要的约束方程个数更多而已。

注意：

在$D$矩阵的构建过程中，需要用到$r^2=x^2+y^2$。而由于张正友标定法不能直接求出焦距$f$，理想的无畸变的归一化的图像坐标$(x,y)$无法求解，造成$D$矩阵无法构建的问题。

以下方案可以作为一种解决方案。

世界坐标系下的标定板角点的坐标$(U,V)$乘上刚体变换矩阵（外参矩阵）即可转化为相机坐标系下的标定板角点坐标$(X,Y,Z)$。
$$\left(\begin{array}{c}X\\ \\ Y\\ \\ Z\end{array}\right)=\left(\begin{array}{ccc}R1& R2& T\end{array}\right)\left(\begin{array}{c}U\\ \\ V\\ \\ 1\end{array}\right)$$
此时，相机坐标系下的标定板角点坐标$(X,Y,Z)$乘上透视投影矩阵可得：
$$Z\left(\begin{array}{c}x\\ \\ y\\ \\ 1\end{array}\right)=\left(\begin{array}{cccc}f& 0& 0& 0\\ & & & \\ 0& f& 0& 0\\ & & & \\ 0& 0& 1& 0\end{array}\right)\left(\begin{array}{c}X\\ \\ Y\\ \\ Z\end{array}\right)$$
其中，$(x,y)$为理想的无畸变的归一化的图像坐标。即为：
$$\begin{gathered} x=\frac{fX}{Z} \\ y=\frac{fY}{Z} \end{gathered}$$
记$R^2=X^2+Y^2$，则有$r^2=x^2+y^2=\frac{f^2{R}^2}{Z^2}$。

代入$Dk=d$中，可得：
$$\left[\begin{array}{cc}(u-u_0)\frac{R^2}{Z^2}& (u-u_0)\frac{R^4}{Z^4}\\ & \\ (v-v_0)\frac{R^2}{Z^2}& (v-v_0)\frac{R^4}{Z^4}\end{array}\right]\left[\begin{array}{c}{f}^2{k}_1\\ \\ f^4{k}_2\end{array}\right]=\left[\begin{array}{c}\hat{u}-u\\ \\ \hat{v}-v\end{array}\right]$$
我们将上式重新记为$D\prime k\prime =d$，此时这个系数矩阵$D\prime$是可以完全求出来的，利用最小二乘法求解$k\prime$为：
$$k\prime =\left[\begin{array}{c}{k}_1\prime \\ \\ k_2\prime \end{array}\right]=\left[\begin{array}{c}{f}^2{k}_1\\ \\ f^2{k}_2\end{array}\right]=(D{\prime }^{T}D\prime {)}^{-1}D{\prime }^{T}d$$
这里解得的$k\prime$虽然不是真正的畸变系数，但是由于焦距$f$是定值，因此$k\prime$也是定值，当求得$k\prime$之后，可以将畸变模型化为：
$$\begin{gathered} \hat{u}-u_0=(u-u_0)(1+k_1\prime \frac{R^2}{Z^2}+k_2\prime \frac{R^4}{Z^4}) \\ \hat{v}-v_0=(v-v_0)(1+k_1\prime \frac{R^2}{Z^2}+k_2\prime \frac{R^4}{Z^4}) \end{gathered}$$
此时可以直接在像素坐标系下对畸变参数进行矫正。

五、L-M算法参数优化

从上述推导过程就可以看出，张正友标定法是有很多近似的，所以仅仅利用上述的过程进行标定误差肯定是很大的。所以张正友标定法还利用L-M（Levenberg-Marquardt）算法对参数进行了优化。

六、相机标定的步骤

1. 准备一个张正友标定法的棋盘格，棋盘格大小已知，用相机对其进行不同角度的拍摄，得到一组图像；

2. 对图像中的特征点如标定板角点进行检测，得到标定板角点的像素坐标值，根据已知的棋盘格大小和世界坐标系原点，计算得到标定板角点的物理坐标值；

3. 求解内参矩阵与外参矩阵；
   根据物理坐标值和像素坐标值的关系，求出$H$矩阵，进而构造$v$矩阵，求解$B$矩阵，利用$B$矩阵求解相机内参矩阵$A$，最后求解每张图片对应的相机外参矩阵$\left(\begin{array}{cc}R& T\\ 0& 1\end{array}\right)$；

4. 求解畸变参数；
   利用$\hat{u},u,\hat{v},v$构造$D$矩阵，计算径向畸变参数；

5. 利用L-M（Levenberg-Marquardt）算法对上述参数进行优化。

七、源代码

python基于opencv的源代码：

Calibration_ZhangZhengyou_Method