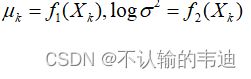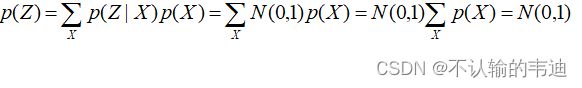生成模型笔记——VAE

摘要

        生成模型中像VAE和GAN，它们的本质目标其实是差不多的，都是希望能够建立一个从隐变量Z生成目标数据X的有效的模型。换句话说，假设存在一些常见的分布Z(如正态分布或者是均匀分布)，然后希望训练出模型使得这个模型他可以将原来的概率分布映射到训练集(如图片)的概率分布；核心思想就是一个概率分布之间的变换。(可查看生成模型笔记预备知识笔记——概率分布变换_不认输的韦迪的博客-CSDN博客)

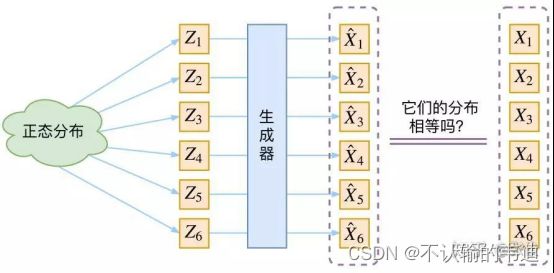
 (这里移用一下知乎的图)图中的大致意思就是从一个正态分布中采样得到经过一个生成器之后变成然后判断这个生成的东西和原来的样本是不是一一相近的。

从这里我们可以看到生成模型的一个比较难处理的问题，就是需要判断从一个正态分布(以流程图为例)采样得到的，经过生成器后(也就是g(z)函数映射)得到的他是什么分布，训练集又是什么分布，就更别提怎么比较这两个是否相等了。总之，这个模型方向是对的，但是就是感觉有点不那么有效。

VAE的初想法

首先还是老问题，我们现在有一批数据样本()我们希望可以在这几个样本熵得到整体X的分布p(x),如果可以做到这个的话，那么我们可以直接根据p(x)来采样得到包括在内的所有样本。用李宏毅老师的课件来说就是如下图所示，给出几个现有小精灵的样本去推出精灵的分布，然后就能知道所有精灵的样本。这个是一个十分理想的模型。

 当然这个理想的模型还是比较难以实现的，但是我们可以对这个进行稍加改造得到：

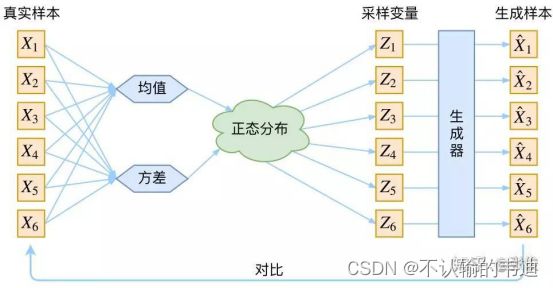
 很明显这个描述了一个由Z来生成X的模型，这里的Z可以是任意的分布，从这个分布Z中我们采样得到一个,并根据这个来算出一个,那么也能达到我们的目标。示意图如下：

 此时我们假设这个Z服从正态分布。

VAE模型

 在上面的流程图中,所有的都从一个正态分布Z中进行采样，但在VAE模型中我们并没有假设p(Z)是一个正态分布，反而是假设p(Z|X)是一个正态分布；更深入地，我们会给每一个真实样本分配一个专属的正态分布，而不像上图那样每一个都从一个正态分布中进行采样；当然我们会假设这个专属的正态分布是（独立的、多元的）。

这样做的好处是什么呢？，由于我们后续会训练一个生成器,希望可以把这个从分布中采样出来的一个还原为;而前期的准备中我们就给了每一个分配了专属的,所以我们有理由说从这个分布中采样出来的应该要还原会对应的中；这个想法可以将上面流程图中遗留的一个很大问题解决，那就是由生成的是不是对应着原来的。

这里格外地提醒一下，我们是假设是服从正态分布的，而非p(Z),虽然在后面的公式推导中可以得出p(Z)也是服从正态分布的，但是在这里需要注意一下。(这也是参考的文章中一个很棒的点)

那好，问题转移到如何为每一个样本分配一个专属的正态分布；咱们知道正态分布有两个参数——均值和方差。如果直接找出这两个值是比较困难的，所以在VAE中选择退而求其次采用神经网络进行对两个值的拟合。通过构建两个神经网络

 选择拟合而不是的原因是因为后者是非负的，是需要添加激活函数的，而前者不需要，因为它可正可负。

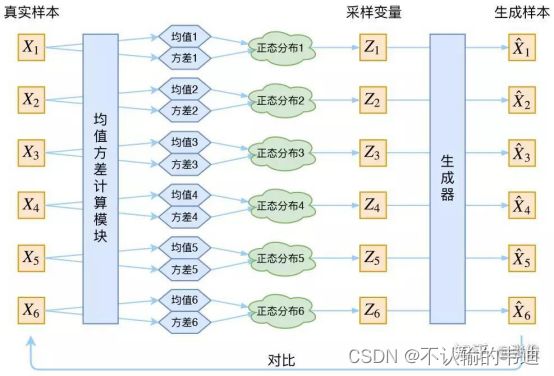
大致的流程如下图所示：

 简单来说，给定一个样本,中间计算均值和方差的神经网络会给出这个样本对应的正态分布，然后我们可以在这个正态分布中去采样，从而得到一个，这个采样得到的在经过生成器这个神经网络就能重新转变为一个与原始样本接近的生成样本.

这样的想法是非常不错的，但是还是存在一点小瑕疵；首先是以正态分布中采样出来的它是存在偏差的(毕竟是采样，会受到方差的影响)，从而导致重构出来的不一定和原来的完全一样。其次无论是第一个神经网络还是第二个神经网络，他们的训练都是依据梯度的，但是采样这个过程就打断了梯度，所以网络还是无法work。上述的流程只是在两个神经网络训练好的理想情况下的流程。

先解决第一个问题。我们知道采样得到的是存在偏差的，而这个偏差是与方差有关的，方差越大每次采样的结果之间也越不接近。一个很简单的想法就是干脆将方差变成0，从正态分布概率密度函数图像上看就是将原先的“小山丘”挤压成一根竖着的“杆子”，这样每次采样只会采到一个固定的值，也就是均值。这样VAE就退化成普通的AutoEncoder了，也就是将高维转成低维再转成高维。而VAE为了保证模型具有生成性(就是可以生成与样本不一样的其他没见过的产出)，让所有的p(Z|X)都往着标准正态分布N(0,1)上靠，这样做的好处是什么呢？如果所有的p(Z|X)都是标准正态分布，那么就有：

 这样的话，采样得到的也是服从标准正态分布的，这样我们就能直接从标准正态分布中直接采样来生成图像了,这就有点像第三张图片中的流程。

对于第二个问题，我们知道每一个都是正态分布,此时我们还没说这个正态分布是标准正态分布，上一段的是模型训练过程中我们希望让这些逐渐接近标准正态分布，相关的训练流程和Loss可以参见原篇。回到这个问题，每一个都是从对应的经过采样得到的，要知道采样的过程它并不可导，因此需要对这个过程进行一个小技巧的实施：

 

 通过这个重参数技巧，我们将从采样转变成从。中采样了。如何理解直接采样没有梯度而重参数之后就又有梯度呢？其实可以这么想，假如我一开始在中采样得到5，但是我完全不知道这个5与之间的关系，在进一步的说，是由神经网络产出的，神经网络中的参数决定了也就是说我更加不知道这个5和之间的关系。但是如果我先从中采样比方得到0.2那么我计算，这样我就能知道Z与，进一步知道Z与之间的关系了。

结尾

 VAE是很重要的一个知识点，但限于我的能力，可能文中存在一些理解偏差，望大佬指出斧正；大家也可以移步变分自编码器VAE：原来是这么一回事 | 附开源代码 - 知乎