【论文阅读】TAPAS: Weakly Supervised Table Parsing via Pre-training

TAPAS: Weakly Supervised Table Parsing via Pre-training

前言

地址：https://arxiv.org/pdf/2004.02349.pdf
本文是在阅读该论文时做的笔记，这里只涉及对原论文的解读，如有不对，欢迎指正交流。本文按照原论文的章节进行解读，并在最后写下自己对该论文的理解和总结。由于最近也在学习Huggingface，在其中也添加了部分的huggingface代码用于加强对该模型的理解。

Abstract

• 通过表格回答自然语言问题通常被视为语义解析任务。为了降低完整逻辑表单的收集成本，一种流行的方法侧重于由表示而不是逻辑表单组成的弱监督。然而，从弱监督中训练语义解析器会带来困难，此外，生成的逻辑形式仅作用检索表示之前的中间步骤。
• 本文提出了TAPAS：
  • 一种在不生成逻辑形式的情况下通过表进行问答的方法
  • 从弱监督中训练，并通过选择表单元格和可选的聚合运算符来预测表意
  • 扩展了BERT结构，将表编码输入，从有效的文本段和从维基百科抓取的表的联合预训练中进行初始化，并进行端到端的训练
• 在三种不同的数据集上进行了实验：
  • SQA 55.1 -> 67.2
  • WIKISQL、WIKITQ 与当前SOTA相当，但用了更简单的模型架构

Introduction

• 从半结构化的表中回答问题通常被视为一种语义解析任务，其中问题会被翻译成一种逻辑形式，可以针对表执行以检索正确的表示法。语义解析器依赖于对自然语言问题和逻辑形式进行配对的监督训练数据，但这种数据的注释成本很高。近年来，也有许多尝试旨在减少语言解析的数据收集负担，一种突出的数据收集方法专注于弱监督，即训练数据由一个问题及其表示法组成，而不是完整的逻辑形式。但由于大量虚假的逻辑形式，导致训练语义解析器很困难。此外，语义解析器只利用生成的逻辑形式作为检索答案的中间步骤。

• 本文提出了TAPAS（表解析器）：

  • 一个弱监督的问答模型，在不生成逻辑表单的情况下对表进行推理。
  • 通过选择表单元格子集及在其上可能执行的聚合操作来预测最小程序
  • 可以从自然语言中学习运算，这是通过扩展BERT的体系结构来实现的。使用额外的嵌入来捕获表格结构，并使用两个分类层来选择单元格和预测相应的聚合运算符。
  • 为TAPAS引入了一种预训练方法，这是它成功完成最终任务的关键。
  • 提出了一种端到端的可微训练方法，允许TAPAS从弱监督训练。

• 接下来通过一小段代码来理解该模型的作用。

from transformers import pipeline
import pandas as pd

tapas = pipeline("table-question-answering",model="google/tapas-base-finetuned-sqa")

data = {
    "Actors": ["Brad Pitt", "Leonardo Di Caprio", "George Clooney"],
    "Age": ["56", "45", "59"],
    "Number of movies": ["87", "53", "69"],
}
table = pd.DataFrame.from_dict(data)
table

我们首先通过Huggingface导入tapas模型，并用代码生成一张表格，如上所示。现在对这个表格有以下三个问题：
–>“How many movies has George Clooney played in?”
–>“How old is Brad Pitt?”
–> “Which actors age are 56 and 59?”
很显然，这些问题的答案可以在上面的表格当中通过一个或多个表单元格得到。因此，可以这样理解tapas的作用，给定一张表格和根据该表格的提出的几个问题，将这些数据丢入tapas模型当中，该模型可以得到正确的答案。

queries = ["How many movies has George Clooney played in?", "How old is Brad Pitt?",
          "Which actors age are 56 and 59?"]
answer = tapas(table=table1,query=queries)  
for ans in answer:
    print(ans)

TAPAS Model

• 模型的体系结构基于BERT的编码器，其中附加了用于编码表格的位置嵌入。添加了两个分类层，用于选择表单元格和进行操作的聚合运算符,如下图所示。
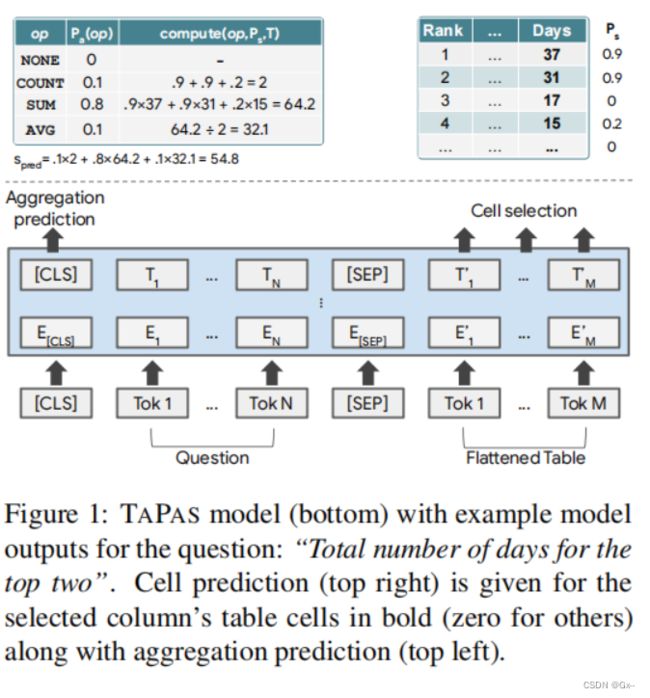  通过上面的描述我们可以知道tapas模型的输入为表格+针对该表格提出的问题，因此如何将这两种数据结构进行表示并输入到模型是首先要解决的一个问题。因此，论文中的解决方案为将表格进行展平后与问题进行拼接，如上图所示。对于对表格进行问答的模型来说，所有问题的答案都来自于表格当中一个或多个表单元格，及表单元格子集。此外，对于一个标量答案来说，其结果有可能是来自于对数个表单元格进行聚合运算后的结果。因此tapas根据上述问题设计了两个头，一个用于选择涉及到的表单元格，一个用于选择对这些表单元格所使用的聚合运算符。第三个问题为原始的表格数据结构中蕴含着丰富的信息，如何将这些信息保留，为此tapas扩展了BERT的编码结构，如下图所示。
  
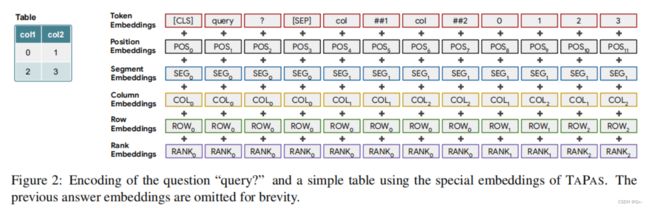
• Addtional embeddings
  • Position ID： 平坦序列中token的索引（与BERT相同）
  • Segment ID： 用于区分问题和表，有两个可能的值。0表示问题，1表示表和单元格
  • Column/Row ID： 该token在表中的行/列索引，0表示问题
  • Rank ID： 如果列值可以被解析为浮点数或日期，对它们进行相应的排序，并根据它们的数值等级（0表示不可比较，1表示最小项，i+1表示等级i的项）分配嵌入
  • Previous Answer： 给定一个对话设置，其中当前问题可能引用前一个问题或其答案，添加一个特殊的嵌入来标记单元token是否是前一个问题的答案(如果token的单元是答案，则为1，否则为0)
• Cell selection： 这个分类层选择表单元格的一个子集
  • 根据所选的聚合运算符，这些单元格可以是最终答案也可以是用于计算最终答案的输入。
  • 首先，使用在最后一个隐藏向量上的线性层计算token的logit，然后计算该单元格中token的平均logit。该层的输出为选择单元格 c 的概率$p_s^{(c)}$
  • 增加了额外的列logit，对应于不选择列或者单元格，将其视为没有单元格的额外列。该层的输出为选择列 co 的概率$p_{col}^{(co)}$，并使用softmax对该列的logit进行计算。将选定列之外的列单元格的$p_s^{(c)}$设为0
• Aggregation operator prediction： 选择聚合运算符
  • 语义解析任务需要对表进行离散推理，例如对数字的求和及对单元格的计数。为了在不产生逻辑表单的情况下处理这些情况，TAPAS输出表单元格的子集以及可选的聚合运算符
  • 聚合运算符用于描述所选单元格的运算，如SUM、COUNT、AVERAGE、NONE
  • 运算符通过一个线性层选择，该层通过在第一个token（特殊[CLS]token）的最后隐藏向量的顶部使用softmax而得。将该层表示为$p_a(op)$，op表示某些运算符
• Inference：
  • 预测最有可能的运算符和表单元格子集（通过cell selection layer)。
  • 为了预测离散单元格的选择，选择概率大于0.5的所有表单元格（即$p_s^{(c)}>0.5$）
  • 然后对表格执行这些预测，通过对所选单元格应用所选的聚合运算符来检索正确答案

对于这一块的理解，个人认为是当一个问题的答案是表格中没有出现过的时候，如下表中的对所有电影总数的求和，其答案是表格中没有出现的，需要经过计算后得到，这时就需要进行推理，即通过上述两个模块选择出相应的表单元格子集和聚合运算符后进行计算得到最后答案。

from transformers import TapasTokenizer, TapasForQuestionAnswering
import pandas as pd

model_name = "google/tapas-base-finetuned-wtq"
model = TapasForQuestionAnswering.from_pretrained(model_name)
tokenizer = TapasTokenizer.from_pretrained(model_name)

data = {"Actors": ["Brad Pitt", "Leonardo Di Caprio", "George Clooney"], "Number of movies": ["87", "53", "69"]}
queries = [
    "What is the name of the first actor?",
    "How many movies has George Clooney played in?",
    "What is the total number of movies?",
]
table = pd.DataFrame.from_dict(data)
table

inputs = tokenizer(table=table, queries=queries, padding="max_length", return_tensors="pt")
outputs = model(**inputs)
predicted_answer_coordinates, predicted_aggregation_indices = tokenizer.convert_logits_to_predictions(
    inputs, outputs.logits.detach(), outputs.logits_aggregation.detach()
)

id2aggregation = {0: "NONE", 1: "SUM", 2: "AVERAGE", 3: "COUNT"}
aggregation_predictions_string = [id2aggregation[x] for x in predicted_aggregation_indices]

answers = []
for coordinates in predicted_answer_coordinates:
    if len(coordinates) == 1:
        # only a single cell:
        answers.append(table.iat[coordinates[0]])
    else:
        # multiple cells
        cell_values = []
        for coordinate in coordinates:
            cell_values.append(table.iat[coordinate])
        answers.append(", ".join(cell_values))


for query, answer, predicted_agg in zip(queries, answers, aggregation_predictions_string):
    print(query)
    if predicted_agg == "NONE":
        print("Predicted answer: " + answer)
    else:
        print("Predicted answer: " + predicted_agg + " > " + answer)

Pre-training

• 为了将预训练模型的成功应用到本次任务中，作为表解析任务的初始化，作者在Wikipedia的大量表格上预训练了TAPAS，这允许模型学习文本和表及列单元和它们的标题直接许多有趣相关性

Fine-tuning

• Overview
  • 在弱监督中正式定义了表解析：
    给定由N个示例$\{(x_i,T_i,y_i){\}}_{i=1}^N$组成的训练集，$x_i$表示一个话语，$T_i$表示一张表，$y_i$表示一个对应的表示集。目标为学习一个模型，该模型将新的话语x映射到程序z，当z针对对应的表T执行时，可以产生正确的表示y。 程序z由单元格子集和可选运算符组成
  • 将每个示例的一组y转换为元组(C,s),C表示单元格的坐标，s是一个标量（仅当y是单个标量时填充）。根据(C,s)的内容指导训练。
• Cell Selection
  • 在这种情况下，y映射到表单元格坐标C的子集（如问题1）。对于这种类型的示例，只使用了一种分层模型，先选择列，再选择该列中的单元格。
  • 直接训练模型选择在C中拥有单元格数量最多的列col。对于我们的数据集来说，单元格C包含在单个列中，所以对模型的这种限制提供了有用的归纳偏差。如果C为空，则选择与空单元格对应的额外空列。然后模型被训练成选择单元格$C\cap col$，而不是选择(T\C)$\cap col$。损失由三部分组成：
    1. 列选择的平均二元交叉熵损失
       $${\mathcal{J}}_{columns}=\frac{1}{|Columns|}\sum _{co\in Columns}CE(p_{col}^{(co)},1_{co=col})$$
       其中列集合包含额外的空列，$CE(\cdot )$是交叉熵损失，$1$是指示函数
    2. 列单元格选择的二元交叉熵损失
       $${\mathcal{J}}_{cells}=\frac{1}{|Cells(col)|}\sum _{co\in Cells(col)}CE(p_s^{(c)},1_{c\in C})$$
       其中Cells(col)是所选列中单元格的集合
    3. 对于没有发生聚合的单元格选择示例，将聚合监督定义为NONE（赋值给$o{p}_0$），聚合损失为
       $${\mathcal{J}}_{aggr}=-\log p_a(o{p}_0)$$
       总损失为 $${\mathcal{J}}_{\mathcal{C}\mathcal{S}}={\mathcal{J}}_{columns}+{\mathcal{J}}_{cells}+\alpha {\mathcal{J}}_{aggr}$$
       $\alpha$是一个缩放超参数
       
• Scalar answer
  • 在这种情况下，y是表中没有出现的单个标量s（即$C=\varnothing$，如问题2）。这通常对应于涉及一个或多个单元格进行聚合的例子。在这项工作中，本文处理与SQL对应的聚合运算符，即COUNT，AVERAGE和SUM，但此模型并不局限于这些
  • 对于这些例子，应该选择的表单元格和聚合运算符是未知的，因为这些不能直接从标量答案s中推断出来。在模型训练中，实现了一个完全可微的层，它可以潜在的学习聚合预测层$pa(\cdot )$的权重。具体来说，本文认识到执行每个受支持的聚合操作符的结果是一个标量。作者为每一个操作符（见下表）实现一个软可微估计，给定选择token的概率及表值。给定所有聚合运算符的结果，然后根据当前模型计算预期结果：$$s_{pred}=\sum _{i=1}{\hat{p}}_a(o{p}_i)\cdot compute(o{p}_i,p_s,T)$$
    其中${\hat{p}}_a(o{p}_i)=\frac{p_a(o{p}_i)}{{\sum }_{i=1}{p}_a(o{p}_i)}$是不包括NONE的聚合运算符上归一化的概率分布
    
  • 然后用Huber损失计算标量答案的损失
    $${\mathcal{J}}_{scalar}=\{\begin{array}{ll}0.5\cdot a^2& a\le \delta \\ \delta \cdot a-0.5\cdot {\delta }^2& otherwise\end{array}$$
    其中$a=|s_{pred}-s|$，$\delta$为超参数。
    此外，由于标量答案意味着一些聚合操作，为此还定义了一个聚合损失，惩罚模型将概率质量分配给NONE类
    $${\mathcal{J}}_{aggr}=-\log (\sum _{i=1}{p}_a(o{p}_i))$$
    总损失为${\mathcal{J}}_{\mathcal{S}\mathcal{A}}={\mathcal{J}}_{aggr}+\beta {\mathcal{J}}_{scalar}$，$\beta$为缩放超参数。对于一些${\mathcal{J}}_{scalar}$可能很大，导致模型不稳定的例子，引入了$cutoff$超参数。然后对于一个${\mathcal{J}}_{scalar}>cutoff$的训练示例,将$\mathcal{J}=0$以完全忽略该示例。
    • Ambiguous answer
  • 在表中出现的标量答案s$(C\ne \varnothing )$有时是模糊的，因为他可能是聚合（问题3），也可能是预测表单元格（问题4）。为此，让模型去动态的根据当前策略选择监督*(cell selection or scalar answer)。* 具体来说，将监督设置为如果$p_a(o{p}_0)\ge S$则为cell selection,其中S (0 < S < 1）是一个阈值超参数,反之为scalar answer。

  Experiments

总结

Tapas发表于2020年，是一篇很值得阅读的关于QA的论文，其代码是开源的。模型采用了新的架构用于对表格进行QA，很好的保留了表格中潜在的数据特征，并且也取得了不错的效果。该模型通过设计两个输出头，可以预测出表格中未出现的数据，单目前只能用于标量答案，对于一些文本答案的预测目前还无法做到。