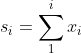MATLAB中对方阵行列式的求解、矩阵的累加和与累乘积进行求解、矩阵的排序、矩阵的秩和迹、以及矩阵的特征值和特征向量的求解
目录
1、方阵的行列式计算
2、累加和与累乘积
(1)累加和
(2)累乘积
3、对于数据进行排序
4、求矩阵的秩
5、矩阵的迹
6、计算矩阵的特征值和特征向量
1、方阵的行列式计算
在线性代数中,对于一个方阵进行求值运算需要先将其转换为行列式,MATLAB中提供过了det函数用于对于方阵的行列式进行求值运算,最后计算得到转换后的行列式的值。
例如:
A=[3,4,8;5,1,9;10,12,4];
B=det(A)计算得到结果为368。
需要注意的是,计算的矩阵必须是一个方阵,否则程序会报错。
2、累加和与累乘积
在数据处理中,经常需要对于所有数据进行累加和以及累乘积进行运算,下面计算在MATLAB对于累加和与累乘积分别进行说明。
(1)累加和
在MATLAB中,第i个元素的累加和指的是从所有数据的第一个开始到第i个元素结束,所有元素的累加之和。假设第i个元素的累加和为![]() ,前面的数据为
,前面的数据为![]() ,那么可以推导出公式如下所示:
,那么可以推导出公式如下所示:
MATLAB中提供了comsum函数计算从第1个元素到第i个元素的累加和,调用格式如下所示(其中V表示向量,A表示矩阵):
- cumsum(V):求解向量V的累加和。
- cumsum(A):如果原矩阵是一个m行n列的矩阵,那么cumsum(A)函数返回一个m行n列的矩阵,矩阵的第i行第j列元素计算的是原矩阵的第j列从第1行元素到第i行元素的累加和。
- cumsum(A,num):当num=1时,效果与cumsum(A)相同,如果原矩阵是一个m行n列的矩阵,那么cumsum(A,1)函数返回一个m行n列的矩阵,矩阵的第i行第j列元素计算的是原矩阵的第j列从第1行元素到第i行元素的累加和。当num=2时,如果原矩阵是一个m行n列的矩阵,那么cumsum(A,2)函数返回的是一个m行n列的矩阵,矩阵的第i行第j列元素计算的是原矩阵的第i行从第1列元素到第j列元素的累加和。
- cumsum(A(:)):计算矩阵中第1个元素到该元素位置的所有元素的累加和,计算顺序是从第一列的每一行进行累加,当第一列全部相加之后,第二列再进行相加……最后一个元素即为矩阵中所有元素的累加和。
例如计算一个向量各个元素的累加和:
V=[2,3,4,5,6,4,6];
x=cumsum(V)运行结果如下所示:
x =
2 5 9 14 20 24 30计算一个矩阵中每一列的元素的从第1行的元素到对应行的元素的累加和。
A=[3,4,5,7;4,9,10,13;13,10,11,24];
x=cumsum(A)运行之后的结果如下所示:
x =
3 4 5 7
7 13 15 20
20 23 26 44
假设原矩阵是一个m行n列的矩阵,计算矩阵每一行从第1列元素开始到第j列元素的累加和以及计算矩阵每一列从第1行到第i行的累加和:
A=[3,4,5,7;4,9,10,13;13,10,11,24];
x=cumsum(A,1)
y=cumsum(A,2)运行结果如下所示:
x =
3 4 5 7
7 13 15 20
20 23 26 44
y =
3 7 12 19
4 13 23 36
13 23 34 58计算矩阵中所有元素的累加和:
A=[32,4,16,20;31,24,15,19;10,12,18,22;41,22,20,26];
x=cumsum(A(:))运算结果如下所示:
x =
32
63
73
114
118
142
154
176
192
207
225
245
265
284
306
332通过上面的结果可以看出,该矩阵的累加和为332。
(2)累乘积
在MATLAB中,第i个元素的累乘积指的是从所有数据的第一元素开始到第i个元素结束,所有元素的累乘之积。假设第i个元素的累乘积为![]() ,前面的数据为
,前面的数据为![]() ,那么可以推导出公式如下所示:
,那么可以推导出公式如下所示:
MATLAB中提供了cumprod函数对于计算从第i个元素到第i个元素的累乘积,调用格式如下所示(其中v表示向量,A表示矩阵):
- cumprod(V):求解向量V的累乘积。
- cumprod(A):如果原矩阵是一个m行n列的矩阵,那么cumprod(A)函数返回一个m行n列的矩阵,矩阵的第i行第j列元素计算的是原矩阵的第j列从第1行元素到第i行元素的累乘积。
- cumprod(A,num):当num=1时,效果与cumprod(A)相同,如果原矩阵是一个m行n列的矩阵,那么cumprod(A,1)函数返回一个m行n列的矩阵,矩阵的第i行第j列元素计算的是原矩阵的第j列从第1行元素到第i行元素的累乘积。当num=2时,如果原矩阵是一个m行n列的矩阵,那么cumprod(A,2)函数返回的是一个m行n列的矩阵,矩阵的第i行第j列元素计算的是原矩阵的第i行从第1列元素到第j列元素的累乘积。
- cumpord(A(:)):计算矩阵中第1个元素到该元素位置的所有元素的累乘积,计算顺序是从第一列开始,每一行进行累乘,当第一列全部相乘之后,第二列再进行相乘……最后一个元素即为矩阵中所有元素的累乘积。
例如计算一个向量各个元素的累乘积:
V=[2,1,3,4,5,2,3];
x=cumprod(V)运行结果如下所示:
x =
2 2 6 24 120 240 720计算一个矩阵中每一列的元素的从第1行元素到对应元素的累乘积:
A=[3,4,5,6;6,2,1,2;4,3,2,1];
x=cumprod(A)运行结果如下所示:
x =
3 4 5 6
18 8 5 12
72 24 10 12假设原矩阵是一个m行n列的矩阵,计算矩阵每一行从第1列元素开始到第j列元素的累乘积以及计算矩阵每一列从第1行元素开始到第i行元素结束的累乘积:
A=[3,4,5,7;4,9,10,13;13,10,11,24];
x=cumprod(A,1)
y=cumprod(A,2)运行结果如下所示:
x =
3 4 5 7
12 36 50 91
156 360 550 2184
y =
3 12 60 420
4 36 360 4680
13 130 1430 34320
计算矩阵中所有元素的累乘积:
A=[2,3,6;8,5,2;9,11,12];
x=cumprod(A(:))运行结果如下所示:
x =
2
16
144
432
2160
23760
142560
285120
3421440在上面的运算结果中,最后一个元素3421440即为矩阵中所有元素的乘积。
3、对于数据进行排序
在进行数据处理的时候,经常需要对于数据进行排序操作,因此编写程序的时候序号对数据进行排序,例如在数据结构就有十大经典排序算法。同样在MATLAB中也提供了sort函数对于数据进行排序操作。
sort函数返回的是一个新的矩阵,默认情况下是从小到大排序的。
- sort(V):对于向量V进行排序,返回的结果是已经从小到大排序好的向量。
- sort(A):对于矩阵的每一列的元素进行排序,返回的是每一列的元素从小到大排序好的矩阵。
- sort(A,num):当num=1的时候,该效果与sort(A)相同,返回的是每一列的元素从小到大排序的好的矩阵;当num=2的时候,对于矩阵的每一行进行排序,返回的结果是每一行的元素从小到大排序好的矩阵。
- sort(A(:)):返回一个列向量,该向量是矩阵所有元素的从小到大依次排序。
例如,下面利用sort函数对于向量进行排序:
V=[34,23,6,41,65,32,7,53];
V=sort(V)运算后的结果如下所示:
V =
6 7 23 32 34 41 53 65可以看到利用sort函数对于向量进行排序之后向量V变成了各个元素从小到大依次排列好的向量。
再例如,利用sort函数对于矩阵每一列进行排序:
A=[2,5,3;6,10,7;4,9,11;12,4,3];
sort(A)运行结果如下所示:
ans =
2 4 3
4 5 3
6 9 7
12 10 11通过上面的运算结果可以看出,sort函数对于矩阵的每一列的元素进行从小到大的排序。
再例如利用sort函数分别对矩阵的每一行和每一列进行排序:
A=[2,5,3;6,10,7;4,9,11;12,4,3];
x=sort(A,1)
y=sort(A,2)运行结果如下所示:
x =
2 4 3
4 5 3
6 9 7
12 10 11
y =
2 3 5
6 7 10
4 9 11
3 4 12通过上面的运算结果可以看出,分别当sort(A,num)的num为1或者2时,是分别对于矩阵的列和行进行排序。
利用sort函数对于矩阵的所有元素进行排序:
A=[2,3,6;8,5,2;9,11,12];
sort(A(:))运行结果如下所示:
ans =
2
2
3
5
6
8
9
11
12
通过运行结果可以看出来,通过sort(A(:))返回的是一个列向量,可以对于矩阵的所有元素进行排序。
4、求矩阵的秩
矩阵的秩是在对于矩阵求线性相关性以及线型方程组的解等问题的一个重要的工具,定义如下:矩阵的秩是线性代数中的一个概念。在线型代数中,一个矩阵A的列秩是线型独立的纵列的极大数,行秩是矩阵的线性无关的横行极大数目。即如果把矩阵看成了一个个行向量或者列向量,秩就是这些行向量和列向量的秩,也就是极大无关组中所含向量的个数。(本段定义来自百度百科矩阵的秩)
在我们实际运算的过程中,一般的运算方式是将矩阵转换为行阶梯型矩阵,计算整行中不是全部为0的行的个数,该个数即为矩阵的秩。
而在MATLAB提供了rank函数用于对于矩阵的秩进行计算,例如:
A=[1,2,3;2,4,6;8,4,7];
rA=rank(A)
B=[23,6,5;6,3,11;7,13,12];
rB=rank(B)运算结果如下所示:
rA =
2
rB =
3通过上面的运算结果显示,A矩阵的秩为2,B矩阵的秩为3,A和B都是三阶矩阵,通过对于矩阵的秩的计算可以得到A是一个满秩矩阵,而B是一个不满秩矩阵。
5、矩阵的迹
对于方阵A来说,方阵对角线上所有对角线之和称为矩阵的迹,即为tr(A),显然矩阵的迹的计算方式为:
![]()
在MATLAB中,提供了trace函数计算矩阵的迹。例如:
A=[4,5,3;7,5,3;9,11,3];
B=trace(A)运算结果如下所示:
B =
126、计算矩阵的特征值和特征向量
特征值的概念是由法国科学家拉普拉斯在19世纪为研究天体力学、地球力学的时候所引进的概念,在实际应用中矩阵的特征值的应用十分广泛。
假设A是一个n阶的矩阵,如果数![]() 和n维非零向量x满足下面的条件:
和n维非零向量x满足下面的条件:
![]()
那么![]() 是方阵A的特征值,非零向量x称为方阵A的对应特征值
是方阵A的特征值,非零向量x称为方阵A的对应特征值![]() 的特征向量。
的特征向量。
上面的公式同样可以写成形式:
![]()
上面的式子有非零解的条件是:
![]()
同样也可以写成如下形式:
在MATLAB中提供了eig函数计算矩阵的特征向量和特征值,调用的格式如下所示:
- e=eig(A):e是一个列向量,计算矩阵A中的所有的特征值。
- [V,R]=eig(A):R是矩阵A的特征值构成的对角矩阵,对角阵R上的元素是矩阵A的所有特征值,而V是A各列相应的特征向量。
利用MATLAB的eig函数计算矩阵的特征值,例如:
A=[0,1,1;1,0,1;1,1,0];
B=[4,5,5;3,6,7;8,9,4];
e1=eig(A)
e2=eig(B)结果如下所示:
e1 =
-1.0000
-1.0000
2.0000
e2 =
17.0296
0.6537
-3.6832
再例如:
A=[12,16,8;9,23,11;24,18,4]
[V,D]=eig(A)运行结果如下所示:
V =
-0.4994 -0.4102 -0.1379
-0.6110 0.5782 -0.3173
-0.6143 -0.7053 0.9382
D =
41.4154 0 0
0 3.1994 0
0 0 -5.6149通过上面的内容可以看出矩阵A的特征值分别为41.4154、3.1994、-5.6149,而矩阵V是矩阵A各列的特征向量。