PyTorch入门到进阶实战笔记二(慕课网)
文章目录
- Pytorch搭建简单神经网络
-
- 机器学习和神经网络的基本概念
- 利用神经网络解决分类和回归问题
-
- 预测房价(回归)
- 手写数字图片分类(分类)
- 计算机视觉
-
- 计算机视觉的基本概念
- 常见的图像处理概念
-
- 亮度、对比度、饱和度
- 图像平滑/降噪
- 图像锐化/增强
- 边缘提取算子
- 直方图均衡化
- 图像滤波
- 形态学运算
- OpenCV及其常用库函数介绍
- 特征工程
-
- 从特征工程的角度理解计算机视觉的常见问题
- 卷积神经网络概念介绍
-
- 卷积层
-
- 常见的卷积操作
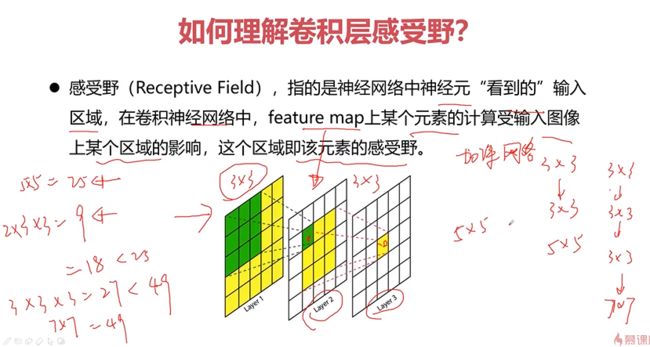
- 如何理解卷积层感受野
- 如何理解卷积层的参数量与计算量
- 如何压缩卷积层参数&计算量
- 常见的卷积层组合结构
- 池化层(pooling层)
- 上采样层
- 激活层
- BatchNorm层
- 全连接层(FC)
- Dropout
- 损失层
- 经典的卷积神经网络结构
-
- 串联结构的典型代表
- 跳连结构的典型代表
- 并行结构的典型代表
- 轻量型网络结构
- 多分支结构的典型代表
- Attention的网络结构
-
- Attention结构的典型代表
-
- 作用在特征图上
- 作用在Channel上
- 学习率
- 优化器
- 卷积神经网添加正则化
-
- 并行结构的典型代表
- 轻量型网络结构
- 多分支结构的典型代表
- Attention的网络结构
-
- Attention结构的典型代表
-
- 作用在特征图上
- 作用在Channel上
- 学习率
- 优化器
- 卷积神经网添加正则化
Pytorch搭建简单神经网络
机器学习和神经网络的基本概念


诊断偏差和方差:
![]()
根据学习曲线判断:
高偏差的学习曲线:
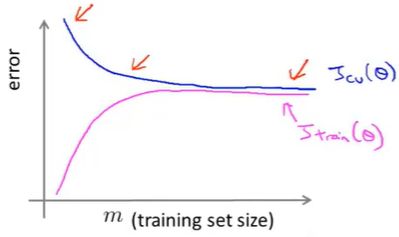
如果一个学习算法有高偏差,随着我们增加训练样本,就是向图片右边移动,我们发现交叉验证误差不会明显地下降了,基本变成平的了;所以如果学习算法正处于高偏差的情形,那么选用更多的训练集数据对于改善算法表现无益
高方差的学习曲线:
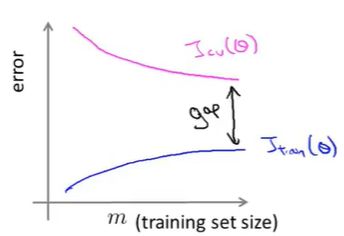
如果我们考虑增加训练集的样本数,两条的学习曲线正在互相靠近,那么在一定程度下,两条曲线会接近相交,那么表示如果学习算法正处于高方差的情况,增加样本数对改进算法是有帮助的

利用神经网络解决分类和回归问题


预测房价(回归)
demo_reg.py
import torch
#data
import numpy as np
import re
ff = open("housing.data").readlines()
data = []
for item in ff:
#将数值间的多个空格合并为一个空格
out = re.sub(r"\s{2,}", " ",item).strip()
#\s匹配空白符 {2,}至少匹配2次 strip()去除收尾空格
#sub()替换
#print(out)
data.append(out.split(" "))
data = np.array(data).astype(np.float) #把列表数据变为数组形式,同时数据变为float格式
print(data.shape)#(506,14)
Y = data[:,-1] #将最后一列Y值取出
X = data[:,0:-1]
#划分测试集和训练集
X_train = X[0:496,...]
Y_train = Y[0:496,...]
X_test = X[496:,...]
Y_test = Y[496:,...]
print("----------数据集维度----------")
print(X_train.shape)
print(Y_train.shape)
print(X_test.shape)
print(Y_test.shape)
print("-----------------------------")
#net
class Net(torch.nn.Module):
def __init__(self, n_feature, n_output):
super(Net,self).__init__()
#加入一层隐藏层,优化欠拟合的问题
self.hidden = torch.nn.Linear(n_feature,100)
self.predict = torch.nn.Linear(100,n_output)
def forward(self,x):
out = self.hidden(x)
out = torch.relu(out)
out = self.predict(out)
return out
#定义了只有一个线性隐藏层的网络
net = Net(13,1) #输入单元13个,输出单元1个
#loss
loss_func = torch.nn.MSELoss() #采用均方损失
#optimiter
#使用Adam优化算法,优化欠拟合的问题
optimizer = torch.optim.Adam(net.parameters(), lr = 0.001)
#training
for i in range(5000):#如果CPU足够可以训练10000次
x_data = torch.tensor(X_train,dtype=torch.float32)
y_data = torch.tensor(Y_train,dtype=torch.float32)
pred = net.forward(x_data)
#print(pred.shape) 二维
#print(y_data.shape) 一维 因此需要统一纬度
pred = torch.squeeze(pred)#压缩维度
loss = loss_func(pred, y_data) * 0.001
optimizer.zero_grad() #将梯度置为零
loss.backward() #进行反向传播
optimizer.step() #更新参数
print("ite:{}, loss_train:{}".format(i,loss))
print(pred[0:10])
print(y_data[0:10])
#如果loss为nan,则可能是学习率过大或者loss过大
#test
x_data = torch.tensor(X_test,dtype=torch.float32)
y_data = torch.tensor(Y_test,dtype=torch.float32)
pred = net.forward(x_data)
pred = torch.squeeze(pred)#压缩维度
loss_test = loss_func(pred, y_data) * 0.001
print("ite:{}, loss_test:{}".format(i,loss_test))
torch.save(net,"model/model.pkl")#保存整个网络
#torch.load("") #加载网络
#torch.save(net.state_dict(), "params.pkl")#只保存参数
#net.load_state_dict("")#此时需要先定义出网络,然后再进行加载参数
demo_reg_inference.py
import torch
'''加载模型完成推理'''
#data
import numpy as np
import re
ff = open("housing.data").readlines()
data = []
for item in ff:
#将数值间的多个空格合并为一个空格
out = re.sub(r"\s{2,}", " ",item).strip()
#\s匹配空白符 {2,}至少匹配2次 strip()去除收尾空格
#sub()替换
#print(out)
data.append(out.split(" "))
data = np.array(data).astype(np.float) #把列表数据变为数组形式,同时数据变为float格式
print(data.shape)#(506,14)
Y = data[:,-1] #将最后一列Y值取出
X = data[:,0:-1]
#划分测试集和训练集
X_train = X[0:496,...]
Y_train = Y[0:496,...]
X_test = X[496:,...]
Y_test = Y[496:,...]
print("----------数据集维度----------")
print(X_train.shape)
print(Y_train.shape)
print(X_test.shape)
print(Y_test.shape)
print("-----------------------------")
#net
class Net(torch.nn.Module):
def __init__(self, n_feature, n_output):
super(Net,self).__init__()
#加入一层隐藏层,优化欠拟合的问题
self.hidden = torch.nn.Linear(n_feature,100)
self.predict = torch.nn.Linear(100,n_output)
def forward(self,x):
out = self.hidden(x)
out = torch.relu(out)
out = self.predict(out)
return out
#加载网络
net = torch.load("model/model.pkl")
#loss
loss_func = torch.nn.MSELoss() #采用均方损失
#test
x_data = torch.tensor(X_test,dtype=torch.float32)
y_data = torch.tensor(Y_test,dtype=torch.float32)
pred = net.forward(x_data)
pred = torch.squeeze(pred)#压缩维度
loss_test = loss_func(pred, y_data) * 0.001
print("loss_test:{}".format(loss_test))
手写数字图片分类(分类)
CNN.py
import torch
#net
#定义只包含一个卷积层和一个FC层的网络
class CNN(torch.nn.Module):
def __init__(self):
super(CNN,self).__init__()
#定义卷积操作
self.conv = torch.nn.Sequential(
torch.nn.Conv2d(1,32,kernel_size=5, padding=2),#输入chanel为1,卷积核为5×5
torch.nn.BatchNorm2d(32)
torch.nn.ReLU(),
torch.nn.MaxPool2d(2)
)
#定义FC层
self.fc = torch.nn.Linear(14 * 14 * 32, 10)#因为有池化操作原来28×28的图像变为14×14;输出在0-9的概率分布,为10维的
def forward(self,x):
out = self.conv(x)
out = out.view(out.size()[0],-1)
out = self.fc(out)
return out
demo_cls.py
import torch
import torchvision.datasets as dataset
import torchvision.transforms as transforms
import torch.utils.data as data_utils
from CNN import CNN
#data
train_data = dataset.MNIST(root="mnist",train=True,
transform=transforms.ToTensor(),download=True)
test_data = dataset.MNIST(root="mnist",train=False,
transform=transforms.ToTensor(),download=False)
#batchsize
train_loader = data_utils.DataLoader(dataset=train_data,
batch_size=64, shuffle=True) #shuffle将数据打乱
test_loader = data_utils.DataLoader(dataset=test_data,
batch_size=64, shuffle=True) #shuffle将数据打乱
cnn = CNN()
cnn = cnn.cuda()
#loss
loss_func = torch.nn.CrossEntropyLoss()#因为是分类问题,所以使用交叉熵的损失函数
#optimizer
optimizer = torch.optim.Adam(cnn.parameters(), lr=0.01)
#training
for epoch in range(10):
for i, (images, lables) in enumerate(train_loader):
images = images.cuda()
labels = labels.cuda()
outputs = cnn(images)
loss = loss_func(outputs, labels)
optimizer.zero_grad()
loss.backward()
optimizer.step()
print("epoch is {}, ite is {}/{}, loss is {}".format(epoch+1,i,
len(train_data)//64,
loss.item())) #item()得到张量的元素值
#test/eval
loss_test = 0
accuracy = 0
for i, (images, lables) in enumerate(test_loader):
images = images.cuda()
labels = labels.cuda()
outputs = cnn(images)
#label的维度[batchsize,1]
#outputs的维度[batchsize * cls_num],因此要计算出概率最大的那个index
loss_test += loss_func(outputs, labels)
_,pred = outputs.max(1)
accuracy += (pred == labels).sum().item()
accuracy = accuracy / len(test_data)
loss_test = loss_test / (len(test_data) // 64)
print("epoch is {},accuracy is {},"
"loss_test is {}".format(epoch+1,
accuracy,
loss_test.item()))
#save
torch.save(cnn,"model/mnist_model.pkl")
demo_cls_inference.py
import torch
import torchvision.datasets as dataset
import torchvision.transforms as transforms
import torch.utils.data as data_utils
from CNN import CNN
#data
test_data = dataset.MNIST(root="mnist",train=False,
transform=transforms.ToTensor(),download=False)
#batchsize
test_loader = data_utils.DataLoader(dataset=test_data,
batch_size=64, shuffle=True) #shuffle将数据打乱
cnn = torch.load("model/mnist_model.pkl")
cnn = cnn.cuda()
#test/eval
loss_test = 0
accuracy = 0
import cv2#导入python版的openCV
for i, (images, lables) in enumerate(test_loader):
images = images.cuda()
labels = labels.cuda()
outputs = cnn(images)
_,pred = outputs.max(1)
accuracy += (pred == labels).sum().item()
images = images.cpu().numpy()
lables = labels.cpu().numpy()
pred = pred.cpu().numpy()
#batchsize * 1 * 28 * 28
for idx in range(images.shape[0]):
im_data = images[idx]
im_label = labels[idx]
im_pred = pred[idx]
print("label",im_label)
print("pred",im_pred)
cv2.imshow("imdata", im_data)
cv2.waitKey(0)
accuracy = accuracy / len(test_data)
print(accuracy)
计算机视觉
计算机视觉的基本概念
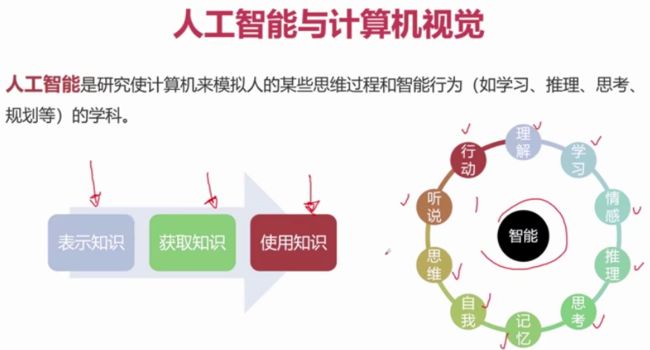
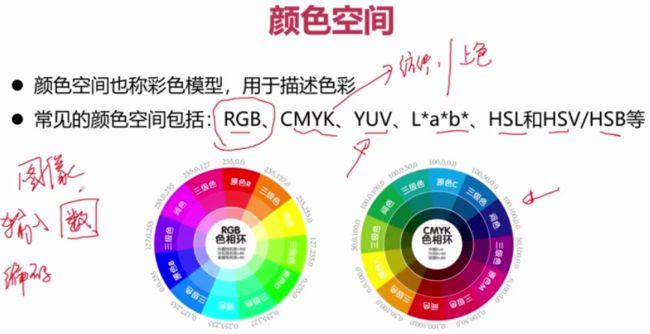


常见的图像处理概念
亮度、对比度、饱和度
图像平滑/降噪

会使边缘点看起来模糊,质量下降
图像锐化/增强

增加边缘信息、轮廓清晰;同时也会增加图像的噪声
边缘提取算子
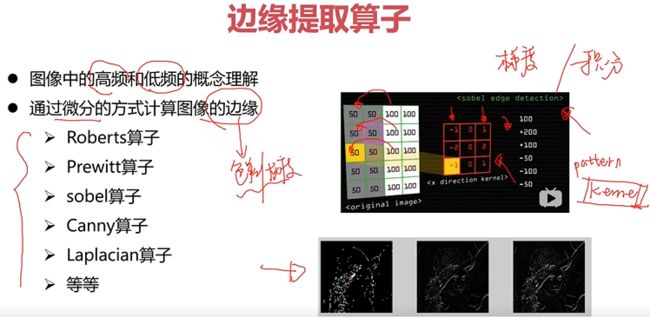
算子:用周围的几个像素作差,定义不同的模板pattern —>kernel
直方图均衡化
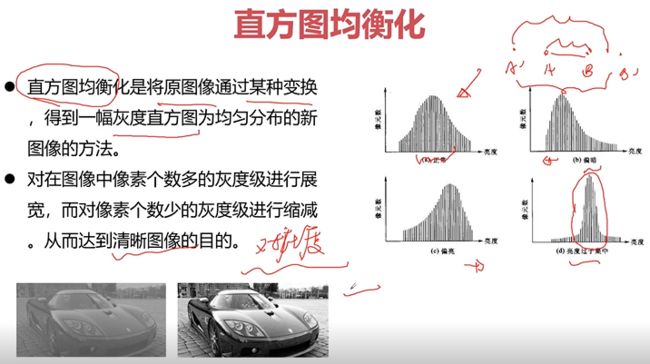
图像滤波

fliter -->滤波器
形态学运算

OpenCV及其常用库函数介绍

特征工程
从特征工程的角度理解计算机视觉的常见问题
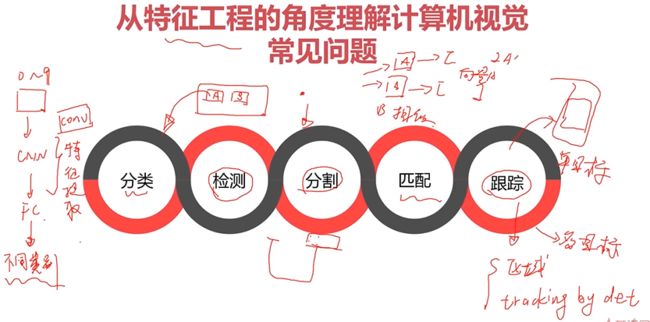
卷积神经网络概念介绍
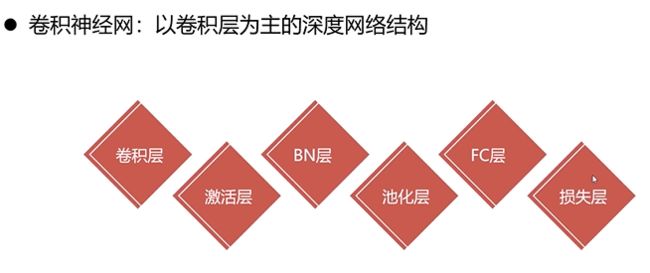
卷积层
![]()
如果步长为2,就作了下采样,几乎缩小了一倍,这时使用padding来对边缘进行填充
滤波矩阵 --> kernel(pattern)
滤波矩阵就像一个滑动的窗口,来对局部区域依次进行滤波,最后得到卷积后的新的特征图。
padding设置使得输出结果尽量是整数倍下采样
常见的卷积操作

如何理解卷积层感受野
这个3×3的区域即为一个感受野
Layer3在Layer1上的感受野为5×5
通过卷积的叠加来增大感受野;使用小的卷积核叠加,这样可以加深网络,增强非线性能力
如何理解卷积层的参数量与计算量

如何压缩卷积层参数&计算量

常见的卷积层组合结构

池化层(pooling层)
通过池化层完成对输入图像的下采样

上采样层
推荐使用Resize进行上采样,这个方法计算简单
激活层
卷积层在实际计算时,类似: y = w x + b y=wx+b y=wx+b是线性运算,这样计算出来后为线性网络。因此会增加激活函数增加非线性
实际运用中,每一个卷积层后都会加一个ReLU层来增加非线性能力

BatchNorm层

可以将BatchNorm层合并入卷积层,这样可以加快计算速度
通常应用时,一个卷积层后跟着一个ReLU层和一个BatchNorm层
全连接层(FC)

通常FC层在使用时会加入dropout来抑制参数
Dropout

减少参数使模型变得简单,达到结构最小化
损失层

经典的卷积神经网络结构
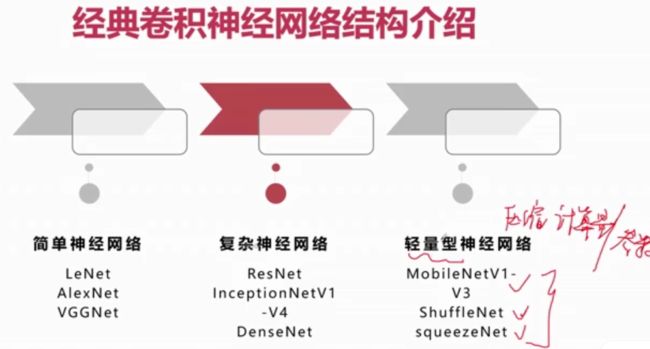
简单神经网络:通常使用的是卷积堆叠
轻量型的神经网络有利于落地实现
串联结构的典型代表
参数量和计算量比较大
跳连结构的典型代表

并行结构的典型代表

轻量型网络结构

多分支结构的典型代表
用来解决相似性任务或者多任务网络结构

Attention的网络结构

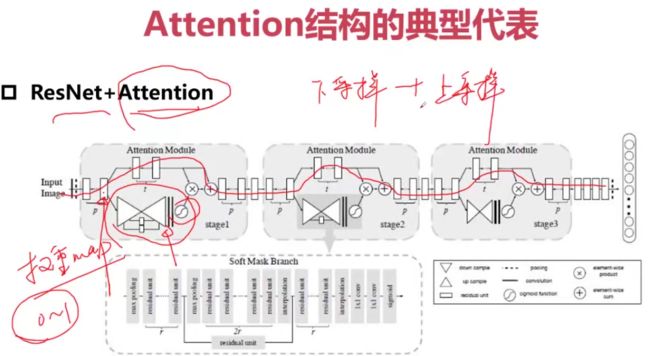
Attention结构的典型代表
作用在特征图上
作用在Channel上
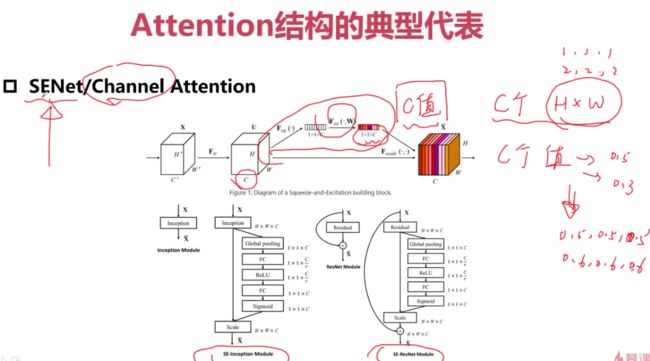
学习率
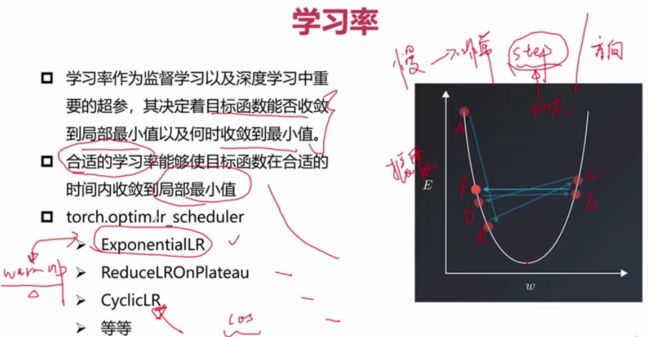
在开始的时候使学习率大一点,之后随着收敛次数学习率不断衰减
优化器

SGD每次只考虑一个样本,收敛不稳定,震荡较大;
MBGD无法保证每次的mini-batch的质量
因此引入动量原则
学习率也很重要,因此我们考虑如何将学习率纳入优化器中,使用自适应学习率来使优化效果更好
实践中经常使用Adam
卷积神经网添加正则化
由于卷积神经网模型比较深,计算量很大,因此收敛稳定性容易有问题,同时也容易发生过拟合;因此一般都会添加正则化
![]()
e=“zoom:80%;” />
并行结构的典型代表

轻量型网络结构

多分支结构的典型代表
用来解决相似性任务或者多任务网络结构

Attention的网络结构

Attention结构的典型代表
作用在特征图上

作用在Channel上

学习率

在开始的时候使学习率大一点,之后随着收敛次数学习率不断衰减
优化器

SGD每次只考虑一个样本,收敛不稳定,震荡较大;
MBGD无法保证每次的mini-batch的质量
因此引入动量原则
学习率也很重要,因此我们考虑如何将学习率纳入优化器中,使用自适应学习率来使优化效果更好
实践中经常使用Adam
卷积神经网添加正则化
由于卷积神经网模型比较深,计算量很大,因此收敛稳定性容易有问题,同时也容易发生过拟合;因此一般都会添加正则化
[外链图片转存中…(img-Yctbc7lD-1616574001500)]