学习笔记：动手学深度学习 04 线性代数

1.标量

标量由只有一个元素的张量表示。

import torch

x = torch.tensor([3.0])
y = torch.tensor([2.0])

x + y, x * y, x / y, x**y

2.向量

通过一维张量处理向量。一般来说，张量可以具有任意长度，取决于机器的内存限制。

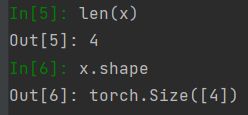
x = torch.arange(4)
x

 

 在代码中，我们通过张量的索引来访问任一元素。

x[3]

 3.长度、维度和形状

4.矩阵

指定两个分量mm和nn来创建一个形状为m×nm×n的矩阵。

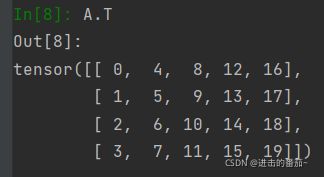
A = torch.arange(20).reshape(5, 4)
A

 

 矩阵转置

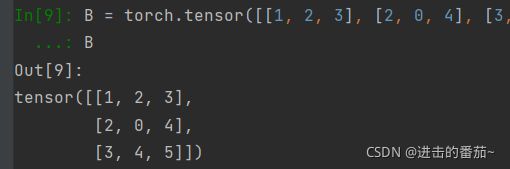
A.T

造一个对称矩阵

B = torch.tensor([[1, 2, 3], [2, 0, 4], [3, 4, 5]])
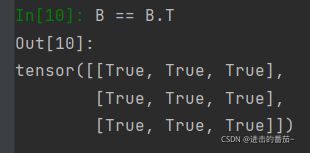
B

对称矩阵的特点

B == B.T

 

 5.张量

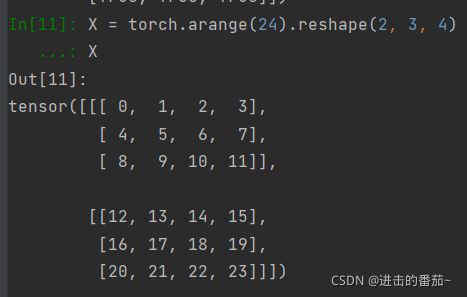
就像向量是标量的推广，矩阵是向量的推广一样，我们可以构建具有更多轴的数据结构。张量（本小节中的“张量”指代数对象）为我们提供了描述具有任意数量轴的nn维数组的通用方法。

X = torch.arange(24).reshape(2, 3, 4)
X

 

6.张量算法的基本性质

标量、向量、矩阵和任意数量轴的张量（本小节中的“张量”指代数对象）有一些很好的属性，通常会派上用场。

两个相同形状的矩阵相加会在这两个矩阵上执行元素加法。

A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
B = A.clone()  # 通过分配新内存，将A的一个副本分配给B
A, B, A + B

具体而言，两个矩阵的按元素乘法称为哈达玛积（Hadamard product）（数学符号⊙⊙）。对于矩阵B∈Rm×nB∈Rm×n，其中第ii行和第jj列的元素是bijbij。

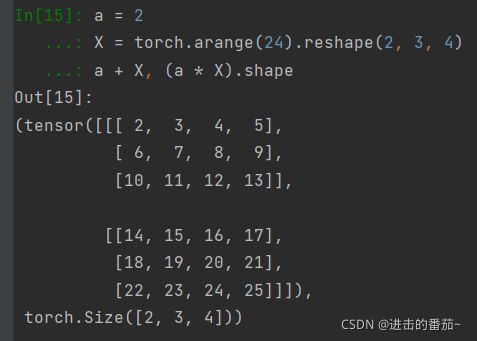
将张量乘以或加上一个标量不会改变张量的形状，其中张量的每个元素都将与标量相加或相乘。

a = 2
X = torch.arange(24).reshape(2, 3, 4)
a + X, (a * X).shape

 7.降维

对任意张量进行的一个有用的操作是计算其元素的和。在数学表示法中，我们使用∑符号表示求和。在代码中，我们可以调用计算求和的函数：

x = torch.arange(4, dtype=torch.float32)
x, x.sum()

我们可以表示任意形状张量的元素和。

可以指定张量沿哪一个轴来通过求和降低维度。

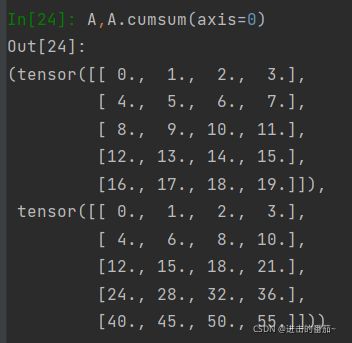
以矩阵为例，为了通过求和所有行的元素来降维（轴0），我们可以在调用函数时指定axis=0。 由于输入矩阵沿0轴降维以生成输出向量，因此输入的轴0的维数在输出形状中丢失。

A_sum_axis0 = A.sum(axis=0)
A_sum_axis0, A_sum_axis0.shape

指定axis=1将通过汇总所有列的元素降维（轴1）。因此，输入的轴1的维数在输出形状中消失。

A_sum_axis1 = A.sum(axis=1)
A_sum_axis1, A_sum_axis1.shape

 

 对行列求和

 

一个与求和相关的量是平均值（mean或average）。我们通过将总和除以元素总数来计算平均值。在代码中，我们可以调用函数来计算任意形状张量的平均值。

  7.非降维求和

但是，有时在调用函数来计算总和或均值时保持轴数不变会很有用。

sum_A = A.sum(axis=1, keepdims=True)
sum_A

由于sum_A在对每行进行求和后仍保持两个轴，我们可以通过广播将A除以sum_A。

如果我们想沿某个轴计算A元素的累积总和，比如axis=0（按行计算），我们可以调用cumsum函数。此函数不会沿任何轴降低输入张量的维度。

8.点积

也就是矩阵相乘

y = torch.ones(4, dtype = torch.float32)
x, y, torch.dot(x, y)

 

注意，我们可以通过执行按元素乘法，然后进行求和来表示两个向量的点积：

9.矩阵-向量积

在代码中使用张量表示矩阵-向量积，我们使用与点积相同的dot函数。当我们为矩阵A和向量x调用np.dot(A,x)时，会执行矩阵-向量积。注意，A的列维数（沿轴1的长度）必须与x的维数（其长度）相同。

左行右列

A.shape, x.shape, torch.mv(A, x)

 

10.矩阵-矩阵乘法

我们可以将矩阵-矩阵乘法ABAB看作是简单地执行mm次矩阵-向量积，并将结果拼接在一起，形成一个n×mn×m矩阵。在下面的代码中，我们在A和B上执行矩阵乘法。这里的A是一个5行4列的矩阵，B是一个4行3列的矩阵。相乘后，我们得到了一个5行3列的矩阵。

B = torch.ones(4, 3)
torch.mm(A, B)

 

 11. 范数

线性代数中最有用的一些运算符是范数（norm）。非正式地说，一个向量的范数告诉我们一个向量有多大。 这里考虑的大小（size）概念不涉及维度，而是分量的大小。

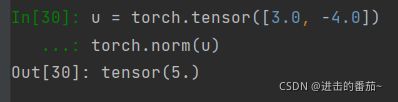
在代码中，我们可以按如下方式计算向量的L2范数。 最简单的范数

u = torch.tensor([3.0, -4.0])
torch.norm(u)

在深度学习中，我们更经常地使用L2范数的平方。你还会经常遇到L1范数，它表示为向量元素的绝对值之和：

为了计算L1范数，我们将绝对值函数和按元素求和组合起来。

torch.abs(u).sum()

torch.norm(torch.ones((4, 9))) 默认P=2