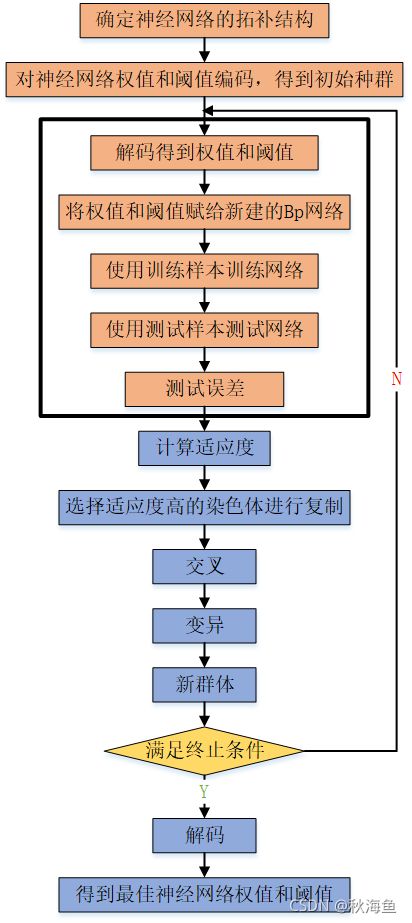
基于遗传算法优化的BP神经网络算法

所用数据同“2 - 较复杂的BP神经网络实现”
GAMain.m

clc
clear 
close all
%% 加载神经网络的训练样本 测试样本每列一个样本 输入P 输出T
%样本数据就是前面问题描述中列出的数据
load dataa
% warning('off')
% 初始隐层神经元个数
%hiddennum=31;
hiddennum=13;
inputnum=size(P1,1);       % 输入层神经元个数
outputnum=size(T1,1);      % 输出层神经元个数
w1num=inputnum*hiddennum; % 输入层到隐层的权值个数=输入层*隐含层节点个数
w2num=outputnum*hiddennum;% 隐层到输出层的权值个数=输出层*隐含层节点个数
N=w1num+hiddennum+w2num+outputnum; %待优化的变量的个数=权值+阈值（隐含层+输出层节点个数）

%% 定义遗传算法参数
NIND=40;        %个体数目，种群大小  #可修改该值来调整优化效果
MAXGEN=100;      %最大遗传代数  #可修改该值来调整优化效果
PRECI=10;       %变量的二进制位数，个体长度                                  ？？如何确定，对优化结果有何影响
GGAP=0.95;      %代沟，95%的父代复制给了子代。GGAP缺省或NaN表示=1，GGAP也可大于1。传统遗传算子包括:选择,交叉,变异；新的遗传算子,如代沟,人工选择等等
px=0.7;         %交叉概率
pm=0.01;        %变异概率
trace=zeros(N+1,MAXGEN);                        %寻优结果的初始值，初始权值和阈值

FieldD=[repmat(PRECI,1,N);repmat([-0.5;0.5],1,N);repmat([1;0;1;1],1,N)];  %区域描述器 ？？

Chrom=crtbp(NIND,PRECI*N);    %初始种群，创建任意离散随机种群矩阵，NIND行PRECI*N列，个体数目*个体长度
%% 优化
gen=0;                                 %代计数器
X=bs2rv(Chrom,FieldD);                 %计算初始种群的十进制转换
ObjV=Objfun(X,P1,T1,hiddennum,P1_test,T1_test);  %计算目标函数值，计算适应度值，  ？？
while gen<MAXGEN
   fprintf('%d\n',gen)
   
   FitnV=ranking(ObjV); %分配适应度值。按照个体的目标值ObjV（列向量）由小到大的顺序对个体进行排序，并返回个体适应度值FitnV的列向量
   
   SelCh=select('sus',Chrom,FitnV,GGAP); %选择。SelCh=select(SEL_F,Chrom,FitnV,GGAP)：
   %SEL_F是一个字符串，包含一个低级选择函数名，如rws或sus。
   %FitnV是列向量，包含种群Chrom中个体的适应度值，该值表明每个个体被选择的预期概率。
   %GGAP是一个可选参数，指出代沟部分种群被复制。若GGAP省略或为NaN，则GGAP=1。
   %SUBPOP是一个可选参数，决定种群Chrom中子种群的数量。若SUBPOP省略或为NaN，则SUBPOP=1，种群Chrom中子种群必须有相同大小。
   
   SelCh=recombin('xovsp',SelCh,px); %交叉。NewChrom=recombin(REC_F,Chrom,RecOpt)。此处为矩阵第一行后四位与第二行后四位交叉
   %REC_F是一个包含低级重组函数名的字符串，如recdis或xovsp
   %RecOpt是一个指明交叉概率的任选参数，若省略或为NaN，将设为缺省值
   
   SelCh=mut(SelCh,pm); %变异。NewChrom=mut(OldChrom,Pm,BaseV)。
   %OldChrom是当前种群
   %Pm为变异概率，省略时为0.7/Lind
   %BaseV指明染色体个体元素的变异的基本字符，省略时为二进制编码
   
   X=bs2rv(SelCh,FieldD);  %子代个体的十进制转换，将二进制转换到十进制。Phen=bs2rv(SelCh,FieldD)
   %bs2rv根据译码矩阵FieldD将二进制串矩阵Chrom转换为实值向量，返回十进制矩阵
   
   ObjVSel=Objfun(X,P1,T1,hiddennum,P1_test,T1_test);  %计算子代的目标函数值，计算子代适应度值
   
   [Chrom,ObjV]=reins(Chrom,SelCh,1,1,ObjV,ObjVSel); %重插入子代到父代，得到新种群
   X=bs2rv(Chrom,FieldD);  %新种群二进制转换到十进制
   gen=gen+1;              %代计数器增加
   %获取每代的最优解及其序号，Y为最优解,I为个体的序号
   [Y,I]=min(ObjV);
   trace(1:N,gen)=X(I,:);    %记下每代的最优值
   trace(end,gen)=Y;         %记下每代的最优值
end
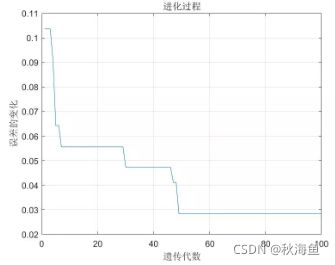
%% 画进化图
figure(1);
plot(1:MAXGEN,trace(end,:));
grid on
xlabel('遗传代数')
ylabel('误差的变化')
title('进化过程')
bestX=trace(1:end-1,end);
bestErr=trace(end,end);
[~,bestT_sim]=BpFunction(bestX,P1,T1,hiddennum,P1_test,T1_test);
fprintf(['最优初始权值和阈值:\nX=',num2str(bestX'),'\n最小误差err=',num2str(bestErr),'\n'])

Objfun.m

function Obj=Objfun(X,P1,T1,hiddennum,P1_test,T1_test)
%% 用来分别求解种群中各个个体的目标值
%% 输入
% X：所有个体的初始权值和阈值
% P：训练样本输入
% T：训练样本输出
% hiddennum：隐含层神经元数
% P_test:测试样本输入
% T_test:测试样本期望输出
%% 输出
% Obj：所有个体的预测样本的预测误差的范数

[M,N]=size(X);
Obj=zeros(M,1);
for i=1:M
%     Obj(i)=Bpfun(X(i,:),P,T,hiddennum,P_test,T_test);
    Obj(i)=BpFunction(X(i,:),P1,T1,hiddennum,P1_test,T1_test);
end

BpFunction.m

%% 输入
% x：一个个体的初始权值和阈值
% P：训练样本输入
% T：训练样本输出
% hiddennum：隐含层神经元数
% P_test:测试样本输入
% T_test:测试样本期望输出
%% 输出
% err：预测样本的预测误差的范数
function [err,T_sim]=BpFunction(x,P1,T1,hiddennum,P1_test,T1_test)
inputnum=size(P1,1);                             % 输入层神经元个数
% hiddennum=2*inputnum+1;                           % 隐含层神经元个数
outputnum=size(T1,1);                                % 输出层神经元个数
%% 数据归一化
[p_train,ps_train]=mapminmax(P1,0,1);
p_test=mapminmax('apply',P1_test,ps_train);
[t_train,ps_output]=mapminmax(T1,0,1);
%% 开始构建BP网络
net=newff(p_train,t_train,hiddennum);               %隐含层为hiddennum个神经元
%设定参数网络参数
net.trainParam.epochs=1000;
net.trainParam.goal=1e-3;
net.trainParam.lr=0.01;
net.trainParam.showwindow=false;                    %高版MATLAB使用 不显示图形框
%% BP神经网络初始权值和阈值
w1num=inputnum*hiddennum;                                           %输入层到隐层的权值个数
w2num=outputnum*hiddennum;                                          %隐含层到输出层的权值个数
% x=2*rand(1,w1num+hiddennum+w2num+outputnum)-1;                      %随即生成权值
W1=x(1:w1num);                                                      %初始输入层到隐含层的权值
B1=x(w1num+1:w1num+hiddennum);                                      %隐层神经元阈值
W2=x(w1num+hiddennum+1:w1num+hiddennum+w2num);                      %隐含层到输出层的权值
B2=x(w1num+hiddennum+w2num+1:w1num+hiddennum+w2num+outputnum);      %输出层阈值
net.iw{1,1}=reshape(W1,hiddennum,inputnum);                         %为神经网络的输入层到隐含层权值赋值
net.lw{2,1}=reshape(W2,outputnum,hiddennum);                        %为神经网络的隐含层到输出层权值赋值
net.b{1}=reshape(B1,hiddennum,1);                                   %为神经网络的隐层神经元阈值赋值
net.b{2}=reshape(B2,outputnum,1);                                   %为神经网络的输出层阈值赋值
%% 开始训练
net = train(net,p_train,t_train);
%% 测试网络
t_sim = sim(net,p_test);
T_sim = mapminmax('reverse',t_sim,ps_output);   %反归一化
err=norm(T_sim-T1_test);                         %预测结果与测试结果差的范数，范数越小说明预测得越准确，如果范数为0，说明预测得完全准确

优化结果：

使用遗传算法优化Bp神经网络权值和阈值的流程图如下：