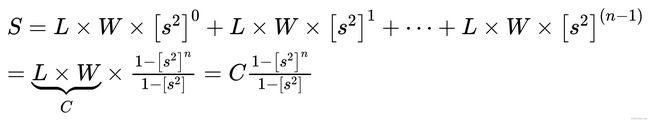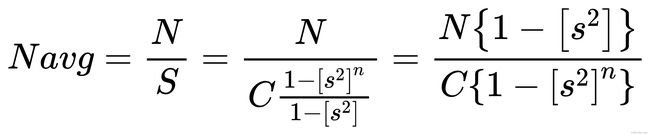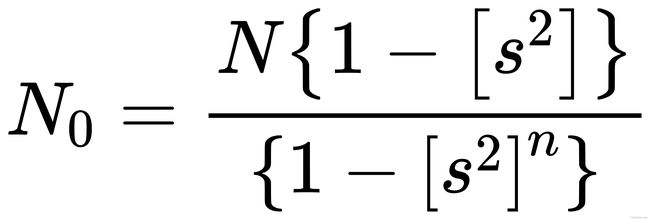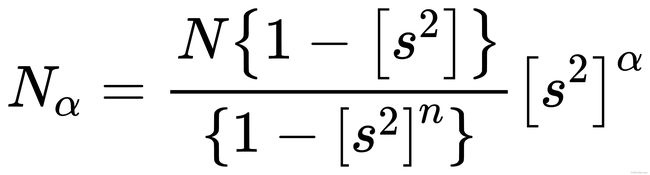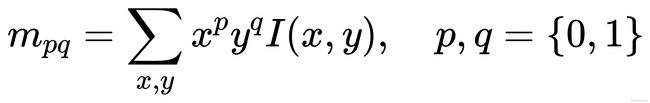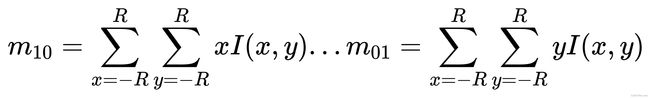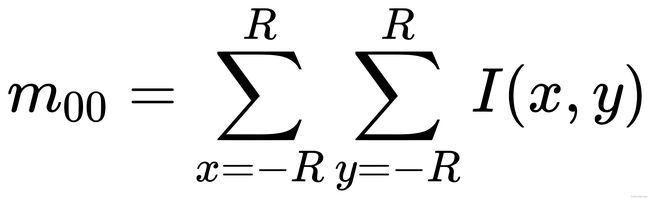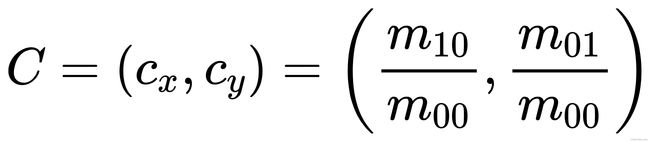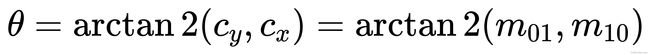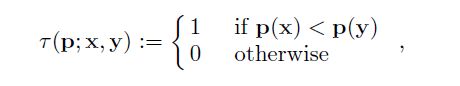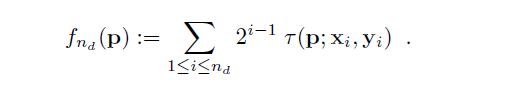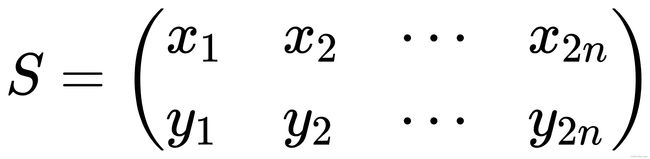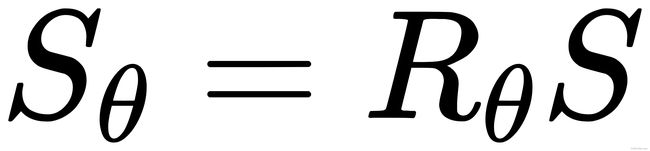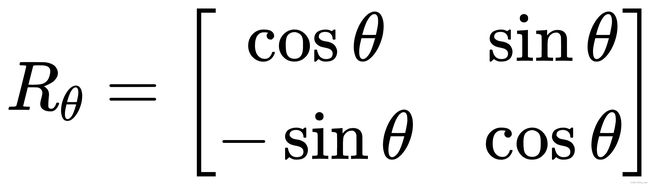ORB-SLAM2源码阅读（一）-----ORB特征提取

前言

1.构建图像金字塔

2. 特征点数量的分配计算

2.1如何分配每一层提取的特征点数量。

2.2什么是FAST角点，如何提取？

3. Oriented FAST，旋转角度计算

4. 计算Rotation-Aware BRIEF， rBRIEF

4.1 BRIEF描述子

4.2 Steered BRIEF

5. 使用四叉树均匀分布特征点---ORB-SLAM对ORB特征的改进

---

前言

ORB-SLAM的一大创新点在于系统的所有模块都使用了同一种特征：ORB，这样构造的系统更加简单、稳健。
本文首先介绍了原版的ORB特征，之后又介绍了ORB-SLAM对ORB特征的改进。

1.一定的尺度不变性：利用图像金子塔实现，由于金字塔层数有限，因此只能在一定范围保证尺度的不变性。

2.旋转不变性：首先利用灰度质心法计算出特征的方向，然后计算旋转后的BRIEF描述子。

3.抗噪能力：计算BRIEF的时候不是使用一个点的灰度，而是使用了点周围5×5区域的灰度。

4.应该也有一定的光照不变性：因为FAST提取的时候是比较灰度，rBRIEF的计算也是比较灰度。

5.速度快：使用了FAST角点，BRIEF描述子，二者均很快。速度是SIFT的100倍，SURF的10倍。

 鉴于对小白友好型，这里给一些理论基础，这些看懂之后再看就非常容易：

全网最详细SIFT算法原理实现

Sift中尺度空间、高斯金字塔、差分金字塔（DOG金字塔）、图像金字塔

---

1.构建图像金字塔

图像金字塔对应函数为：void ORBextractor::ComputePyramid(cv::Mat image)

    int nfeatures;			            ///<整个图像金字塔中，要提取的特征点数目
    double scaleFactor;		            ///<图像金字塔层与层之间的缩放因子
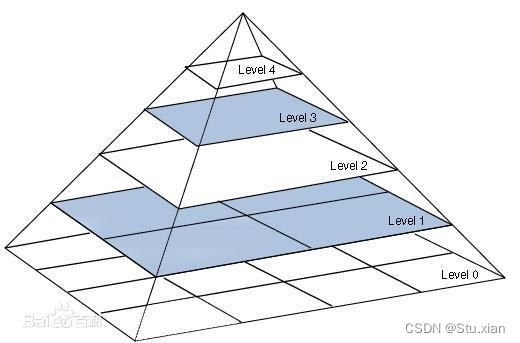
    int nlevels;			            ///<图像金字塔的层数

 对一张图像进行连续的等比缩放(一般是缩小)，把多次缩放之后的图像加上原图，我们统称为图像金字塔，注意这里使用的是图像金字塔，并非高斯金字塔（应用在SIFT中）。

目的：在获取目标图像后计算图像金字塔（nlevels张不同分辨率的图片），为FAST关键点在各层上的计算提供支持。

实质：在不同的尺度空间上查找关键点，并计算出关键点的方向。

 其上的 Level 0 表示原图， Level 1 则为 按照缩放因子 f 进行第一次缩放的结果，Level 2 则是在 Level 1 的基础上，按照放因子 f 再次进行缩放之后的结果。这样一次循环叠加，形成了上面的图像金字塔。使用图像金字塔，我们可以提取到图像各个尺寸的关键点，这样增加了算法的鲁棒性。

---

2. 特征点数量的分配计算

2.1如何分配每一层提取的特征点数量。

金字塔层数越高，图像的面积越小，所能提取到的特征数量就越小。基于这个原理，我们可以按照面积将特征点均摊到金字塔每层的图像上。我们假设第0层图像的宽为 ，长为 ，缩放因子为 （这里的 ）。那么整个金字塔总的面积为

 那么，单位面积的特征点数量为

那么，第0层应分配的特征点数量为 

 接着那么，推出了第 α 层应分配的特征点数量为

 实际上，OpenCV里的代码不是按照面积算的，而是按照边长来算的。也就是上面公式中的 [s2] 换成 s 。

[ORB-SLAM2] ORB-SLAM中的ORB特征（提取） - 知乎

2.2什么是FAST角点，如何提取？

FAST角点，通过对比中心与周围点（半径为3的圆上的点）灰度的差别，即可确定是否为关键点，速度贼快

 至于FAST算法的原理这里不过多的赘述可以参考：Features From Accelerated Segment Test

按照上述步骤对图像上每个像素处理一遍，可以获取大量的FAST角点。那，FAST角点容易出现扎堆现象，要用非极大值抑制再处理一遍（Non-maximal suppression）。TODO: NMS具体实施。非极大值抑制的方法使用的分数计算很简单，计算一个中心点与周围16个点灰度差绝对值的和最为分数：

为了选择响应最大的个角点，还需要计算一个Harris响应。最后，在每层中选择响应最大的 个特征点。TODO： Harris角点的计算。

---

3. Oriented FAST，旋转角度计算

原始的FAST关键点没有方向信息，当图像发生旋转后，brief描述子也会发生变化使得特征点对旋转不鲁棒。

解决办法：使用灰度质心法计算特征点的方向。（Oriented FAST）

灰度质心法：

（1）我们定义该区域图像的矩为：

在半径为R 的圆形图像区域，沿两个坐标轴 x,y方向的图像矩分别为：

圆形区域内所有像素的灰度值总和为：

图像的质心为：

第 3 步：然后关键点的 “ 主方向 ” 就可以表示为从圆形图像形心 指向质心 的方向向量 于是关键点的旋转角度记为:

至此，不仅仅提取了FAST角点，还找出了角点的角度。这个角度可以用来指导描述子的提取，保证每次都在相同的方向上计算描述子，实现角度不变性。

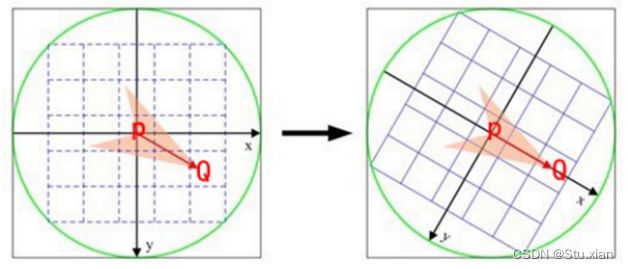
 下图P为几何中心，Q为灰度质心

ORB-SLAM2中的函数： 

 * @brief 这个函数用于计算特征点的方向，这里是返回角度作为方向。
 * 计算特征点方向是为了使得提取的特征点具有旋转不变性。
 * 方法是灰度质心法：以几何中心和灰度质心的连线作为该特征点方向
 * @param[in] image     要进行操作的某层金字塔图像
 * @param[in] pt        当前特征点的坐标
 * @param[in] u_max     图像块的每一行的坐标边界 u_max
 * @return float        返回特征点的角度，范围为[0,360)角度，精度为0.3°
static float IC_Angle(const Mat& image, Point2f pt,  const vector & u_max)

---

4. 计算Rotation-Aware BRIEF， rBRIEF

上述过程，只是找到关键点并确定了其方向，但ORB算法核心用途在于图像的匹配，我们需要对关键点进行数学层面的特征描述，也就是构建关键点描述符.

4.1 BRIEF描述子

1. 以特征点为中心，取其大小为SxS的邻域p(S的大小paper中并为提及，也未讨论S的大小对结果的影响，但是通过原作者之后做的实验中发现，原作者使用的S大小为31)。
2. 在这个区域p中选取nd个点对nd(x,y)，定义τ：

   

     3.p(x)为x点的像素值大小。也就是比较x,y点的像素值，如果y点像素值大则为1，否则为0。 （nd=128，256和512）

     将nd个结果从最低位到最高位依次组成字符串fnd( p)，

 这样把256个点对的结果排起来，就形成了BRIEF描述子。

BRIEF的匹配采用汉明距离，非常快，简单说就是看一下不相同的位数有多少个。如下的两个描述子，不同的位数为4。实际上我们选择的点对数为256，那么距离范围就是0~256。

4.2 Steered BRIEF

BRIEF描述子是没有考虑旋转不变性的，Steered BRIEF根据Oriented FAST计算出的角度，把原始的256个点对的坐标旋转之后，再取灰度。从而实现了旋转不变性。

对于任何一个特征点来说，它的BRIEF描述子是一个长度为nn的二值码串，这个二值串是由特征点周围nn个点对（2n2n个点）生成的，现在我们将这2n2n个点(xi,yi),i=1,2,⋯,2n(xi,yi),i=1,2,⋯,2n组成一个矩阵S

ORB中采用了一个更有效的方法：使用邻域方向θθ和对应的旋转矩阵RθRθ，构建SS的一个校正版本Sθ

 原始的256个点对坐标为 S ，旋转后的为 Sθ 。

 这里可以参考：Oriented FAST and Rotated BRIEF-特征点的描述

5. 使用四叉树均匀分布特征点---ORB-SLAM对ORB特征的改进

ORB-SLAM中并没有使用OpenCV的实现，因为OpenCV的版本提取的ORB特征过于集中，会出现扎堆的现象。这会降低SLAM的精度，对于闭环来说，也会降低一幅图像上的信息量。

ORB 特征提取策略对 ORB-SLAM2 性能的影响： ORB-SLAM2 中的 ORB 特征提取方法相对于 OpenCV 中的方法，提高了 ORB-SLAM2 的轨迹精 度和鲁棒性。增加特征提取的均匀性可以提高系统精度，但是似乎会降低特征提取的重复性。

具体参考：ORB特征提取策略对ORB-SLAM2性能的影响

ORB-SLAM中的实现提高了特征分布的均匀性。 

最简单的一种方法是把图像划分成若干小格子，每个小格子里面保留质量最好的n个特征点。这种方法看似不错，实际上会有一些问题。当有些格子里面能够提取的数量不足n个的时候（无纹理区域），整幅图上提取的特征总量就达不到我们想要的数量。严重的情况下，SLAM就会跟丢喽，ORB-SLAM中的实现就解决了这么一个问题，当一个格子提取不到FAST点的时候，自动降低阈值。ORB-SLAM主要改进了FAST角点提取步骤。

对应函数 DistributeOctTree

 * @brief 使用四叉树法对一个图像金字塔图层中的特征点进行平均和分发
 * @param[in] vToDistributeKeys     等待进行分配到四叉树中的特征点
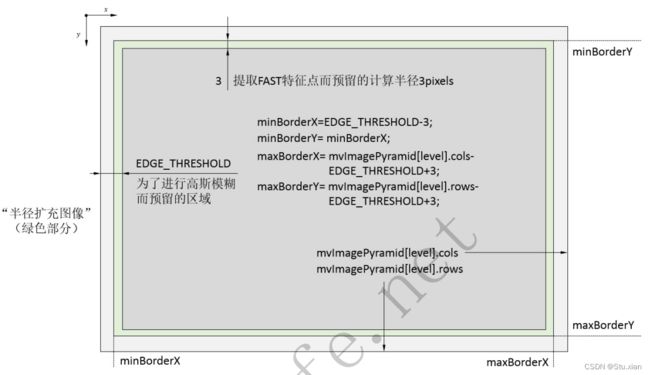
 * @param[in] minX                  当前图层的图像的边界，坐标都是在“半径扩充图像”坐标系下的坐标
 * @param[in] maxX 
 * @param[in] minY 
 * @param[in] maxY 
 * @param[in] N                     希望提取出的特征点个数
 * @param[in] level                 指定的金字塔图层，并未使用
 * @return vector     已经均匀分散好的特征点vector容器
 */
vector ORBextractor::DistributeOctTree(const vector& vToDistributeKeys, const int &minX,
                                       const int &maxX, const int &minY, const int &maxY, const int &N, const int &level)

1. 对于金字塔的每一层。划分格子，格子的大小为30×30pixels
2. 单独对每个格子提取FAST角点，如果提取不到点，就降低FAST阈值。这样保证纹理较弱的区域也能提取到一些FAST角点。这一步可以提取大量的FAST点。
3. 基于四叉树，均匀的选取 Na 个FAST点。

1. 如果图片的宽度比较宽，就先把分成左右w/h份。一般的640×480的图像开始的时候只有一个node。
2. 如果node里面的点数>1，把每个node分成四个node，如果node里面的特征点为空，就不要了，删掉。
3. 新分的node的点数>1，就再分裂成4个node。如此，一直分裂。
4. 终止条件为：node的总数量> Na ，或者无法再进行分裂。
5. 然后从每个node里面选择一个质量最好的FAST点。

图示表示的更清晰一些：

然后： 

 本文章只做学术共享，无其他目的。主要参考这位大佬的内容。

 参考：[ORB-SLAM2] ORB-SLAM中的ORB特征（提取）