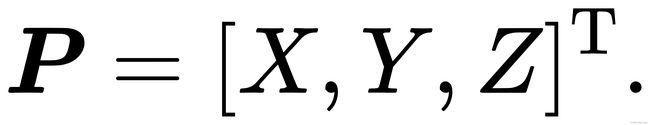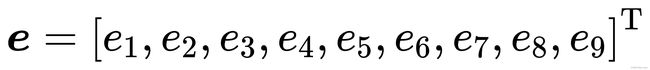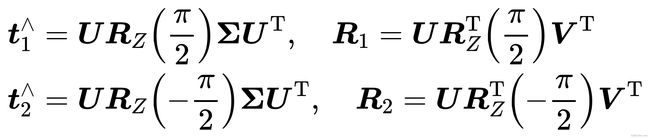视觉里程计-SLAM十四讲学习笔记
一个SLAM系统分为前端和后端,其中前端也称为视觉里程计。视觉里程计根据相邻图像的信息估计出粗略的相机运动,给后端提供较好的初始值。视觉里程计的算法主要分为两个大类:特征点法和直接法。
经典SLAM模型中以相机位姿-路标来描述SLAM过程:
—路标是三维空间中固定不变的点,可以在特定位姿下观测到
—在视觉SLAM中,可利用图像特征点作为SLAM中的路标
特征点是图像当中具有代表性的部分,如轮廓点,较暗区域中的亮点,较亮区域中的暗点等。
—可重复性:相同的区域可以在不同的图像中找到—可区别性:不同的区域有不同的表达
—高效率:同一图像中,特征点的数量应该小于像素的位置—本地性:特征仅与一小片图像区域有关
特征点信息
关键点:指该特征点在图像的位置,大小,朝向等信息。
描述子:特征点周围的周围信息。(通常是一个向量)
常用人工设计更加稳定的局部图像特征:SIFT,SURF, ORB等。简单介绍其原理:
SIFT
SIFT即尺度不变特征变换,是用于图像处理领域的一种描述。这种描述具有尺度不变性,可在图像中检测出关键点,是一种局部特征描述子。
具体可以参考这篇文章:
SIFT原理介绍
ORB
ORB算法介绍
计算相机运动
对极几何 2D-2D
对极约束
假设从两张图像中得到一对配对好的特征点,以图7-9为例,我们希望求取两帧图像![]() ,
,![]() 之间的运动,设第一帧到第二帧的运动为R,t。两个相机中心分别为O1,O2。现在考虑
之间的运动,设第一帧到第二帧的运动为R,t。两个相机中心分别为O1,O2。现在考虑![]() ,中有一个特征点
,中有一个特征点![]() ,它在
,它在![]() 中对应着特征点
中对应着特征点![]() 。我们知道两者是通过特征匹配得到的。如果匹配正确,说明它们确实是同一个空间点在两个成像平面上的投影。
。我们知道两者是通过特征匹配得到的。如果匹配正确,说明它们确实是同一个空间点在两个成像平面上的投影。
![]()
代数分析:在第一帧的坐标系下,设P的空间位置为:
根据相机模型,我们可以知道两个像素点![]() ,
,![]() 的位置为:(这里K为相机内参矩阵,R,t为两个坐标系的相机运动)
的位置为:(这里K为相机内参矩阵,R,t为两个坐标系的相机运动)
尺度意义相等:在使用齐次坐标时,一个向量将等于它自身乘上任意的非零常数,这通常用于表达一个投影关系。这种关系意义为尺度意义下相等。记作:![]() .那么上述投影关系可以写成:
.那么上述投影关系可以写成:![]() .
.
现在我们取![]() (这里两个像素点为归一化平面上的坐标)带入上式可得:
(这里两个像素点为归一化平面上的坐标)带入上式可得:![]() 。
。
两边同时左乘![]() ,这相当于两侧同时与t做外积:
,这相当于两侧同时与t做外积:
让后两边同乘以![]() :
:
化简得:
重新带入 ![]() ,
,![]() ,有:
,有:
这两个式子都成为对极约束,其几何意义![]() 三者共面。对极约束中同时包含了平移和旋转,我们把中间部分记作两个矩阵:基础矩阵F和本质矩阵E,于是进一步简化得:
三者共面。对极约束中同时包含了平移和旋转,我们把中间部分记作两个矩阵:基础矩阵F和本质矩阵E,于是进一步简化得:
于是,相机位姿估计问题变为以下两步:1.根据配对点的像素位置求出E或者F。2.根据E或者F求出R,t。
本质矩阵:(E=![]() R)
R)
·性质1:E满足对极约束。由于对极约束是等式为零的约束,所以对E乘以任意非零常数后,对极约束依然满足。则称为E在不同尺度下是等价的(尺度等价性)。
·性质2:根据E= t^R,可以证明3],本质矩阵E的奇异值必定是[o,o,0]T的形式。这称为本质矩阵的内在性质。
·性质3:另外,由于平移和旋转各有3个自由度,故tR共有6个自由度。但由于尺度等价性,故E实际上有5个自由度。
如何求本质矩阵E呢,我们采用经典的八点法(使用八个点来估计E)
考虑一对匹配点,它们的归一化坐标为![]() ,根据对极约束,有:
,根据对极约束,有:
我们把矩阵E展开,写成向量的形式:
那么,对极约束可以写成与e有关的线性形式::
接下来问题,已估得本质矩阵E,通过奇异值分解计算出相机的运动R,t.设E的SVD 为
奇异值分解(SVD)原理详解及推导
其中U,V为正交阵,习为奇异值矩阵。根据E的内在性质,我们知道![]() [对角矩阵]。在SVD分解中,对于任意一个E,存在两个可能的t,R与它对应:
[对角矩阵]。在SVD分解中,对于任意一个E,存在两个可能的t,R与它对应: