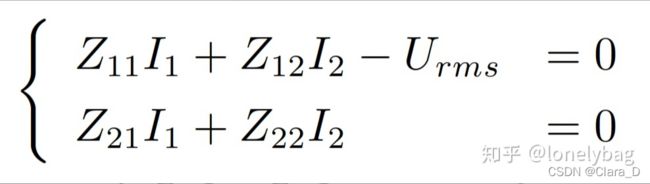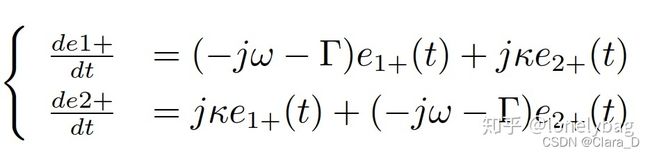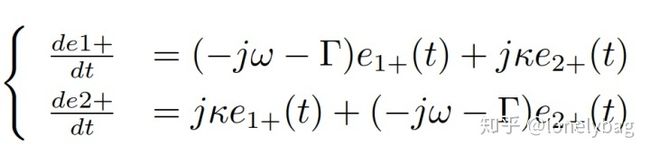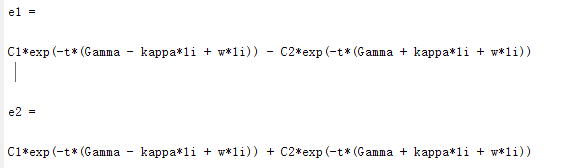转 | 使用Matlab求解数值解

摘要

我们都知道Matlab功能强大，是平时做科研做项目不可缺少的帮手。
但是有的时候使用不熟练确实会走一些弯路，本贴用来记录一下今天在用Matlab求解数值解遇到的问题，概括来说，就是求解数值解的时候不要用solve函数，它是试图求符号解，非常慢，而且相当一部分方程本身没有符号解。
尽管很多博客介绍solve函数的时候会提到也可以求数值解，如 vpasolve函数，但还是建议大家对Matlab求解函数有更多的了解。如 fzero函数和 fsolve函数 等数值方法求。

举例

问题简述：我用已知变量值代入等式之后求得的值，反过来用solve函数无法求出改已知变量。
详述如下：
首先，我运行下面的代码之后，可以得到当tao1=2.0333e-5时的phi值，Matlab求出来此时phi=67.1789。
clear all;
close all;
clc;
Fc=2e3;
Kvco=30e6;
Icp=4e-3;
Kpc=Icp;
N=23200;
gama=1.136;
Wc=2piFc;
tao31=0.6;
tao1=2.0333e-5; % UserVar
phi=(atan(gama/(Wctao1(1+tao31))-atan(Wctao1)-atan(Wctao1tao31)))/pi180

但实际我应用这个程序是已知phi的情况下求解tao1，于是我把代码改成了如下：

clear all;
close all;
clc;
Fc=2e3;
Kvco=30e6;
Icp=4e-3;
Kpc=Icp;
N=23200;
PM=67.1789;
gama=1.136;
Wc=2piFc;
phi=(pi/180)PM;
syms tao1;
tao31=0.6;
tao1=vpasolve(phi==atan(gama/(Wctao1*(1+tao31))-atan(Wctao1)-atan(Wctao1*tao31)),tao1,[0 1])

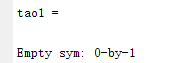
计算得不到tao1=2.0333e-5。

得到Matlab论坛TouAkira回复如下：
论坛的《 常见问题归纳（超链接，自己点进去看） 》等帖子里面都有相关讲解。

简单讲就是，超越方程、复杂方程不要用 solve函数 求，它是试图求符号解，会非常慢，而且相当一部分方程本身没有符号解。直接改用 fzero函数 或 fsolve函数等数值方法求。

很多论坛用户有个典型错觉，“MATLAB是万能的，随便一个积分都能算出解析表达式、随便一个方程都能解出解析表达式”。

薛定宇教授：
接触过众多非数学专业的本科生、研究生、博士生，感觉大多学生缺乏对应用数学问题的较全面了解，他们对什么问题能用数学描述、什么样的数学问题能求解不清楚，以至于在学习与研究中走了很多弯路。

实际上很多积分求不出对应的解析表达式，复杂方程如超越方程、简单多项式方程如一元五次方程，是不可能算出根的公式（即解析表达式）的。

《 得不到具体的解析式 1（超链接，自己点进去看） 》
《 得不到具体的解析式 2（超链接，自己点进去看） 》

超越方程、复杂方程不要指望用 solve函数 就能一劳永逸地求出目标未知量的解析表达式，**要知道能求出解析解的方程是极少数，大部分工程或科研中遇到的超越方程是求不出解析解的。**所以复杂方程往往只能数值逼近（全部参数都代入具体数值，使用数值求解器 fzero函数 或 fsolve函数 等计算）。

Matlab方程求解

以下内容转载自知乎：https://zhuanlan.zhihu.com/p/72537912

1. 线性方程组

1.1. 数值解

syms x y
[x ,y]=solve(y= =2*x+3,y= =3*x-7)

1.2. 符号解

syms Z11 Z12 Z21 Z22 I1 I2 Urms % 定义符号变量

eq_1 = Z11 * I1 + Z12 * I2 - Urms; %方程等号右侧默认为0
eq_2 = Z21 * I1 + Z22 * I2;

[I1 ,I2] = solve(eq_1 , eq_2 , I1 , I2 )

得到输出为：

I1 =
 
(Urms*Z22)/(Z11*Z22 - Z12*Z21)
 
 
I2 =
 
-(Urms*Z21)/(Z11*Z22 - Z12*Z21)

1.3. 化简

syms Z11 Z12 Z21 Z22 I1 I2 Urms 
eq_1 = Z11 * I1 + Z12 * I2 - Urms; %方程等号右侧默认为0

[I1] = solve(eq_1) 

得到输出：

I1 =
 
(Urms - I2*Z12)/I1

2. 微分方程组

2.1. 数值解

freq = 1e6 ;
w = 2 * pi * freq ;

R1 = 0.3 ;
L1 = 1e-6 ;
Gamma = R1 / (2 * L1) ;

k = 0.1 ;
kappa = w * k / 2 ;

%% 求解微分方程组
f = @(t , x) ([(-1i * w - Gamma) * x(1) + 1i * kappa * x(2);...
    1i * kappa * x(1) + (-1i * w - Gamma) * x(2) ]) ;
[t , x]=ode45( f , [0/freq 15/freq] , [0.4e-2 0]) ;

其中，f 为待求解的方程组，[0/freq 15/freq] 表示求解时间为 0 至第 15 个周期，[0.4e−2 0]表示初始边界条件。

2.2. 符号解

[e1 , e2] = dsolve('De1 = (-1i*w - Gamma) * e1 + 1i * kappa * e2' ,...
 'De2 = 1i * kappa * e1 + (-1i * w - Gamma) * e2')

指定初值

[e1 , e2] = dsolve('De1 = (-1i*w - Gamma) * e1 + 1i * kappa * e2' ,...
 'De2 = 1i * kappa * e1 + (-1i * w - Gamma) * e2' , 'e1(0) = 0.4e-2' , 'e2(0) = 0')

注意：

De1的自变量默认为时间t，如果需要求解的是对其他变量的微分，那么需要指明，如：

dsolve('Dy = 3*x*x' , 'x')

D2y 表示y对时间的二次导数

3. 其他

如果希望定义一些符号参与符号运算，如：pi ，就需要显式地事先定义

pi = sym(pi)