高精度惯导初始对准—精对准

前言

高精度惯导的初始对准一般包括粗对准和精对准两个过程，粗对准是一个解析计算的过程，精对准一般使用卡尔曼滤波来实现，本文测试了使用了捷联惯导导航系速度作为观测的精对准算法，其本质相当于一个零速修正的过程，可以估计出陀螺和加表的零偏。最后分析了精对准系统的可观性。

使用的数据集的百度网盘链接如下：

数据集的百度网盘链接

提取码：4ik8

代码

主函数代码如下：

close all;

% 精对准算法测试：

% 车载测试数据
% 静止状态：0-670s
load lb_memsfoggps_ppp_20210414020704;

glvs
ts = mean(diff(imuFOG(:,end)));
t0 = 100; t1 = 300; t2 = 520; 
att0 = aligni0(imuFOG(t0/ts:t1/ts,:), gps(1,4:6)');

att2_ref = aligni0(imuFOG(t1/ts:t2/ts,:), gps(1,4:6)'); % 参考
avp0 = [att0; getat(gps,t1)];

idx = (t1/ts:t2/ts)';
%% vn-meas. Kalman filter
% 初始姿态角，方位角

% 设置失准角P矩阵
phi = [.5;.5;5]*glv.deg;

% 设置IMU噪声，噪声含义如下：
% 陀螺仪偏置：0.5deg/h (设置初始零偏，设置P矩阵)
% 加速度计偏置：500ug[1mg] (设置初始零偏，设置P矩阵)
% 陀螺仪高斯噪声： 0.01deg/sqrt(h)
% 加速度计高斯噪声：25ug/sqrt(Hz)
imuerr = imuerrset(0.5, 500, 0.01, 25);
% 观测速度噪声 ：单位0.1m/s
wvn = [0.1;0.1;0.1];
[att0v, attkv, xkpkv] = alignvn2(imuFOG(t1/ts:t2/ts,:), att0, avp0(7:9), phi, imuerr, wvn, ts,att2_ref);

% myfigure;
% subplot(421); plot(t, attk(:,1:2)/glv.deg); xygo('pr'); title('姿态角'); % 姿态角
% hold on;
% 
% subplot(423); plot(t, attk(:,3)/glv.deg); xygo('y'); title('方位角');% 方位角

alignvn函数如下所示：

function [att0, attk, xkpk] = alignvn2(imu, qnb, pos, phi0, imuerr, wvn, ts,att_ref)
% SINS initial align uses Kalman filter with vn as measurement.
% Kalman filter states: 
%    [phiE,phiN,phiU, dvE,dvN,dvU, ebx,eby,ebz, dbx,dby,dbz]'.
%
% Prototype: [att0, attk, xkpk] = alignvn(imu, qnb, pos, phi0, imuerr, wvn, ts)
% Inputs: imu - IMU data
%         qnb - coarse attitude quaternion
%         pos - position
%         phi0 - initial misalignment angles estimation
%         imuerr - IMU error setting
%         wvn - velocity measurement noise (3x1 vector)
%         ts - IMU sampling interval
% Output: att0 - attitude align result
%         attk, xkpk - for debug
%
% Example:
%	avp0 = [[0;0;0], zeros(3,1), glv.pos0];
%	imuerr = imuerrset(0.03, 100, 0.001, 10);
%	imu = imustatic(avp0, 1, 300, imuerr);
%	phi = [.5; .5; 5]*glv.deg;
%	wvn = [0.01; 0.01; 0.01];
%	[att0, attk, xkpk] = alignvn(imu, avp0(1:3)', avp0(7:9)', phi, imuerr, wvn);
%
% See also  alignfn, alignfn9, aligncmps, aligni0, alignWahba, alignsb, insupdate, etm.

% Copyright(c) 2009-2014, by Gongmin Yan, All rights reserved.
% Northwestern Polytechnical University, Xi An, P.R.China
% 17/06/2011
global glv
    if nargin<4,  phi0 = [1.5; 1.5; 3]*glv.deg;  end
    if nargin<5,  imuerrset(0.01, 100, 0.001, 1);  end
    if nargin<6,  wvn = [0.01; 0.01; 0.01];  end
    if nargin<7,  ts = imu(2,7)-imu(1,7);  end
    if length(qnb)==3, qnb=a2qua(qnb); end  %if input qnb is Eular angles.
    nn = 2; nts = nn*ts;
    len = fix(length(imu)/nn)*nn;
    % Cnn?
    eth = earth(pos); vn = zeros(3,1); Cnn = rv2m(-eth.wnie*nts/2);
    % 滤波器初始化
    kf = avnkfinit(nts, pos, phi0, imuerr, wvn);
    [attk, xkpk] = prealloc(fix(len/nn), 4, 2*kf.n);
    ki = timebar(nn, len, 'Initial align using vn as meas.');
    for k=1:nn:len-nn+1
        wvm = imu(k:k+nn-1,1:6);
        % phim：角度增量
        % dvbm：速度增量
        [phim, dvbm] = cnscl(wvm);
        Cnb = q2mat(qnb);
        % 注意：不进行位置更新！！！
        % 速度更新方程
        dvn = Cnn*Cnb*dvbm;
        vn = vn + dvn + eth.gn*nts;
        %qnb = qupdt(qnb, phim-Cnb'*eth.wnin*nts);
        % 四元数更新方程
        qnb = qupdt2(qnb, phim, eth.wnin*nts);
        Cnbts = Cnb*nts;
        % kf.Phikk_1:状态转移矩阵[时变矩阵]
        kf.Phikk_1(4:6,1:3) = askew(dvn);
        % 陀螺零偏转到导航坐标系
        kf.Phikk_1(1:3,7:9) = -Cnbts;  % 参考公式（7.2.3）
        % 加表零偏转到导航坐标系
        kf.Phikk_1(4:6,10:12) = Cnbts; % 参考公式（7.2.3）
        % 卡尔曼滤波核心函数    
        kf = kfupdate(kf, vn);
        
        % 状态向量更新
        qnb = qdelphi(qnb, 0.1*kf.xk(1:3));  % 部分反馈校正
        kf.xk(1:3) = 0.9*kf.xk(1:3);
        vn = vn-0.1*kf.xk(4:6);  
        kf.xk(4:6) = 0.9*kf.xk(4:6);
        
        attk(ki,:) = [q2att(qnb)',imu(k+nn-1,end)];
        xkpk(ki,:) = [kf.xk; diag(kf.Pxk)];
        ki = timebar;
    end
    attk(ki:end,:) = []; xkpk(ki:end,:) = [];
    att0 = attk(end,1:3)';
    resdisp('Initial align attitudes (arcdeg)', att0/glv.deg);
    avnplot(nts, attk, xkpk,att_ref);
    
function kf = avnkfinit(nts, pos, phi0, imuerr, wvn)
    eth = earth(pos); wnie = eth.wnie;
    kf = []; kf.s = 1; kf.nts = nts;
    % kf.Qt：预测噪声
    % 状态变量： 12状态：失准角,速度,陀螺零偏,加速度计零偏
    % imuerr.sqg:一阶马尔科夫噪声，这里是0
    % imuerr.sqa:一阶马尔科夫噪声，这里是0
    % imuerr.web:陀螺仪高斯噪声
    % imuerr.wdb:加速度计高斯噪声
	kf.Qk = diag([imuerr.web; imuerr.wdb; zeros(6,1)])^2*nts;
    kf.Gammak = 1;
	kf.Rk = diag(wvn)^2;
    
    % kf.Pxk：协方差矩阵设置
    % phi0：失准角：phi = [.5;.5;5]*glv.deg;
    % [1;1;1]：速度初始误差：1m/s
    % imuerr.eb：陀螺仪零偏
    % imuerr.db：加速度计零偏
	kf.Pxk = diag([phi0; [1;1;1]; imuerr.eb; imuerr.db])^2;
	Ft = zeros(12); 
    Ft(1:3,1:3) = askew(-wnie);  % 参考公式（7.2.3）
    % 连续域到离散域
    kf.Phikk_1 = eye(12)+Ft*nts;
	kf.Hk = [zeros(3),eye(3),zeros(3,6)]; % 速度观测【不作差】
    
    [kf.m, kf.n] = size(kf.Hk);
    kf.I = eye(kf.n);
    kf.xk = zeros(kf.n, 1);
    kf.adaptive = 0; % 不自适应卡尔曼滤波
    kf.xconstrain = 0; 
    kf.pconstrain = 0;
    kf.fading = 1;

function avnplot(ts, attk, xkpk,att_ref)
global glv
    t = (1:length(attk))'*ts;
    myfigure;
	subplot(421); plot(t, attk(:,1:2)/glv.deg); xygo('pr'); title('姿态角'); % 姿态角
    hold on; plot(t(end),att_ref(1:2)'/glv.deg,'k*');
	subplot(423); plot(t, attk(:,3)/glv.deg); xygo('y'); title('方位角');% 方位角
    hold on; plot(t(end),att_ref(3)'/glv.deg,'k*');   
	
    subplot(425); plot(t, xkpk(:,7:9)/glv.dph); xygo('eb'); title('状态向量：陀螺零偏误差'); % 状态向量：陀螺零偏误差
	subplot(427); plot(t, xkpk(:,10:12)/glv.ug); xygo('db'); title('状态向量：加表零偏误差'); % 状态向量：加表零偏误差
	subplot(422); plot(t, sqrt(xkpk(:,13:15))/glv.min); xygo('phi'); title('P矩阵：失准角');% P矩阵：失准角
	subplot(424); plot(t, sqrt(xkpk(:,16:18))); xygo('dV'); title('P矩阵：速度误差'); % P矩阵：速度误差
	subplot(426); plot(t, sqrt(xkpk(:,19:21))/glv.dph); xygo('eb'); title('P矩阵：陀螺零偏'); % P矩阵：陀螺零偏
 	subplot(428); plot(t, sqrt(xkpk(:,22:24))/glv.ug); xygo('db'); title('P矩阵：加表零偏'); % P矩阵：加表零偏

结果

粗对准的结果如下：

-6.0147 1.0430 -51.9448

精对准的结果如下：

-6.0120 1.0445 -51.9222

零偏估计结果如下：


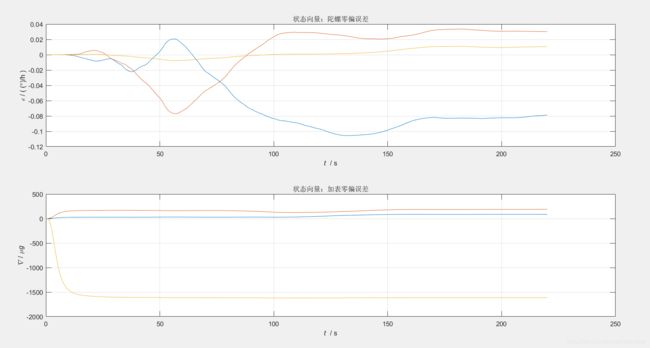
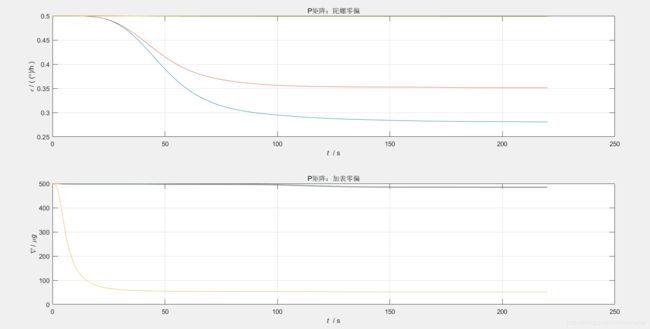
对于加表来说，确实可以通过P矩阵看到E,N是不可观的，U是可观测的，而对于陀螺来说，应该是E是不可观测的，但是在图中并不能直观地看出来。

可观性分析

可观性分析代码如下，可以在alignvn函数中实现。

   % 去掉哪一个状态变量
        remove_idx  = 12;
        % 备注：状态变量12维
        % 可观性分析
        Phikk_1 = kf.Phikk_1([1:remove_idx-1,remove_idx+1:12],:);
        Phikk_1 = Phikk_1(:,[1:remove_idx-1,remove_idx+1:12]);
        
        Hk = kf.Hk(:,[1:remove_idx-1,remove_idx+1:12]);
        Q = [Hk];
        Q = [Q;Hk*Phikk_1];
        Q = [Q;Hk*Phikk_1^2];
        Q = [Q;Hk*Phikk_1^3];
        Q = [Q;Hk*Phikk_1^4];
        Q = [Q;Hk*Phikk_1^5];
        Q = [Q;Hk*Phikk_1^6];
        Q = [Q;Hk*Phikk_1^7];
        Q = [Q;Hk*Phikk_1^8];
        Q = [Q;Hk*Phikk_1^9];
        Q = [Q;Hk*Phikk_1^10];
       % Q = [Q;Hk*Phikk_1^11];
        rank_Q = rank(Q);
        fprintf("rank_Q = %d\n",rank_Q);

开始阶段状态向量为12维：失准角（3），速度误差（3），陀螺零偏（3），加表零偏（3），计算得到的全状态可观性矩阵的秩为9，但是不太清楚哪些状态量是可观的，哪些是不可观的。接下来去掉一个状态变量，看秩的变化，结果如下所示：

% 全状态：9
% 去掉1:8
% 去掉2:8
% 去掉3:8
% 去掉4:7
% 去掉5:7
% 去掉6:7
% 去掉7:9
% 去掉8:9
% 去掉9:9
% 去掉10:9
% 去掉11:9
% 去掉12:9

从上面的结果中还是可以看到一些规律的，失准角对应的是8，速度误差对应的是7，陀螺和加表零偏对应的是9。通过严老师书中的分析可知，速度误差直接来源自量测，失准角对应量测的一次导数，其他是二次导数或者三次导数，导数的阶数越高，对应的可观测度越差。和上述的结果基本一致，从另外一个侧面可以反应可观测度。