Multivariate Time Series Forecasting with LSTMs in Keras
Multivariate Time Series Forecasting with LSTMs in Keras
By Jason Brownlee on August 14, 2017 in Deep Learning for Time Series
Neural networks like Long Short-Term Memory (LSTM) recurrent neural networks are able to almost seamlessly model problems with multiple input variables.
This is a great benefit in time series forecasting, where classical linear methods can be difficult to adapt to multivariate or multiple input forecasting problems.
In this tutorial, you will discover how you can develop an LSTM model for multivariate time series forecasting with the Keras deep learning library.
After completing this tutorial, you will know:
- How to transform a raw dataset into something we can use for time series forecasting.
- How to prepare data and fit an LSTM for a multivariate time series forecasting problem.
- How to make a forecast and rescale the result back into the original units.
Kick-start your project with my new book Deep Learning for Time Series Forecasting, including step-by-step tutorials and the Python source code files for all examples.
Let’s get started.
- Update Aug/2017: Fixed a bug where yhat was compared to obs at the previous time step when calculating the final RMSE. Thanks, Songbin Xu and David Righart.
- Update Oct/2017: Added a new example showing how to train on multiple prior time steps due to popular demand.
- Update Sep/2018: Updated link to dataset.
- Update Jun/2020: Fixed missing imports for LSTM data prep example.
Tutorial Overview
This tutorial is divided into 4 parts; they are:
- Air Pollution Forecasting
- Basic Data Preparation
- Multivariate LSTM Forecast Model
- LSTM Data Preparation
- Define and Fit Model
- Evaluate Model
- Complete Example
- Train On Multiple Lag Timesteps Example
Python Environment
This tutorial assumes you have a Python SciPy environment installed. I recommend that youuse Python 3 with this tutorial.
You must have Keras (2.0 or higher) installed with either the TensorFlow or Theano backend, Ideally Keras 2.3 and TensorFlow 2.2, or higher.
The tutorial also assumes you have scikit-learn, Pandas, NumPy and Matplotlib installed.
If you need help with your environment, see this post:
- How to Setup a Python Environment for Machine Learning
1. Air Pollution Forecasting
In this tutorial, we are going to use the Air Quality dataset.
This is a dataset that reports on the weather and the level of pollution each hour for five years at the US embassy in Beijing, China.
The data includes the date-time, the pollution called PM2.5 concentration, and the weather information including dew point, temperature, pressure, wind direction, wind speed and the cumulative number of hours of snow and rain. The complete feature list in the raw data is as follows:
- No: row number
- year: year of data in this row
- month: month of data in this row
- day: day of data in this row
- hour: hour of data in this row
- pm2.5: PM2.5 concentration
- DEWP: Dew Point
- TEMP: Temperature
- PRES: Pressure
- cbwd: Combined wind direction
- Iws: Cumulated wind speed
- Is: Cumulated hours of snow
- Ir: Cumulated hours of rain
We can use this data and frame a forecasting problem where, given the weather conditions and pollution for prior hours, we forecast the pollution at the next hour.
This dataset can be used to frame other forecasting problems.
Do you have good ideas? Let me know in the comments below.
You can download the dataset from the UCI Machine Learning Repository.
Update, I have mirrored the dataset here because UCI has become unreliable:
- Beijing PM2.5 Data Set
Download the dataset and place it in your current working directory with the filename “raw.csv“.
2. Basic Data Preparation
The data is not ready to use. We must prepare it first.
Below are the first few rows of the raw dataset.
No,year,month,day,hour,pm2.5,DEWP,TEMP,PRES,cbwd,Iws,Is,Ir 1,2010,1,1,0,NA,-21,-11,1021,NW,1.79,0,0 2,2010,1,1,1,NA,-21,-12,1020,NW,4.92,0,0 3,2010,1,1,2,NA,-21,-11,1019,NW,6.71,0,0 4,2010,1,1,3,NA,-21,-14,1019,NW,9.84,0,0 5,2010,1,1,4,NA,-20,-12,1018,NW,12.97,0,0
| 1 2 3 4 5 6 |
No,year,month,day,hour,pm2.5,DEWP,TEMP,PRES,cbwd,Iws,Is,Ir 1,2010,1,1,0,NA,-21,-11,1021,NW,1.79,0,0 2,2010,1,1,1,NA,-21,-12,1020,NW,4.92,0,0 3,2010,1,1,2,NA,-21,-11,1019,NW,6.71,0,0 4,2010,1,1,3,NA,-21,-14,1019,NW,9.84,0,0 5,2010,1,1,4,NA,-20,-12,1018,NW,12.97,0,0 |
The first step is to consolidate the date-time information into a single date-time so that we can use it as an index in Pandas.
A quick check reveals NA values for pm2.5 for the first 24 hours. We will, therefore, need to remove the first row of data. There are also a few scattered “NA” values later in the dataset; we can mark them with 0 values for now.
The script below loads the raw dataset and parses the date-time information as the Pandas DataFrame index. The “No” column is dropped and then clearer names are specified for each column. Finally, the NA values are replaced with “0” values and the first 24 hours are removed.
The “No” column is dropped and then clearer names are specified for each column. Finally, the NA values are replaced with “0” values and the first 24 hours are removed.
from pandas import read_csv from datetime import datetime # load data def parse(x): return datetime.strptime(x, '%Y %m %d %H') dataset = read_csv('raw.csv', parse_dates = [['year', 'month', 'day', 'hour']], index_col=0, date_parser=parse) dataset.drop('No', axis=1, inplace=True) # manually specify column names dataset.columns = ['pollution', 'dew', 'temp', 'press', 'wnd_dir', 'wnd_spd', 'snow', 'rain'] dataset.index.name = 'date' # mark all NA values with 0 dataset['pollution'].fillna(0, inplace=True) # drop the first 24 hours dataset = dataset[24:] # summarize first 5 rows print(dataset.head(5)) # save to file dataset.to_csv('pollution.csv')
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
from pandas import read_csv from datetime import datetime # load data def parse(x): return datetime.strptime(x, '%Y %m %d %H') dataset = read_csv('raw.csv', parse_dates = [['year', 'month', 'day', 'hour']], index_col=0, date_parser=parse) dataset.drop('No', axis=1, inplace=True) # manually specify column names dataset.columns = ['pollution', 'dew', 'temp', 'press', 'wnd_dir', 'wnd_spd', 'snow', 'rain'] dataset.index.name = 'date' # mark all NA values with 0 dataset['pollution'].fillna(0, inplace=True) # drop the first 24 hours dataset = dataset[24:] # summarize first 5 rows print(dataset.head(5)) # save to file dataset.to_csv('pollution.csv') |
Running the example prints the first 5 rows of the transformed dataset and saves the dataset to “pollution.csv“.
pollution dew temp press wnd_dir wnd_spd snow rain date 2010-01-02 00:00:00 129.0 -16 -4.0 1020.0 SE 1.79 0 0 2010-01-02 01:00:00 148.0 -15 -4.0 1020.0 SE 2.68 0 0 2010-01-02 02:00:00 159.0 -11 -5.0 1021.0 SE 3.57 0 0 2010-01-02 03:00:00 181.0 -7 -5.0 1022.0 SE 5.36 1 0 2010-01-02 04:00:00 138.0 -7 -5.0 1022.0 SE 6.25 2 0
| 1 2 3 4 5 6 7 |
pollution dew temp press wnd_dir wnd_spd snow rain date 2010-01-02 00:00:00 129.0 -16 -4.0 1020.0 SE 1.79 0 0 2010-01-02 01:00:00 148.0 -15 -4.0 1020.0 SE 2.68 0 0 2010-01-02 02:00:00 159.0 -11 -5.0 1021.0 SE 3.57 0 0 2010-01-02 03:00:00 181.0 -7 -5.0 1022.0 SE 5.36 1 0 2010-01-02 04:00:00 138.0 -7 -5.0 1022.0 SE 6.25 2 0 |
Now that we have the data in an easy-to-use form, we can create a quick plot of each series and see what we have.
The code below loads the new “pollution.csv” file and plots each series as a separate subplot, except wind speed dir, which is categorical.
from pandas import read_csv from matplotlib import pyplot # load dataset dataset = read_csv('pollution.csv', header=0, index_col=0) values = dataset.values # specify columns to plot groups = [0, 1, 2, 3, 5, 6, 7] i = 1 # plot each column pyplot.figure() for group in groups: pyplot.subplot(len(groups), 1, i) pyplot.plot(values[:, group]) pyplot.title(dataset.columns[group], y=0.5, loc='right') i += 1 pyplot.show()
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
from pandas import read_csv from matplotlib import pyplot # load dataset dataset = read_csv('pollution.csv', header=0, index_col=0) values = dataset.values # specify columns to plot groups = [0, 1, 2, 3, 5, 6, 7] i = 1 # plot each column pyplot.figure() for group in groups: pyplot.subplot(len(groups), 1, i) pyplot.plot(values[:, group]) pyplot.title(dataset.columns[group], y=0.5, loc='right') i += 1 pyplot.show() |
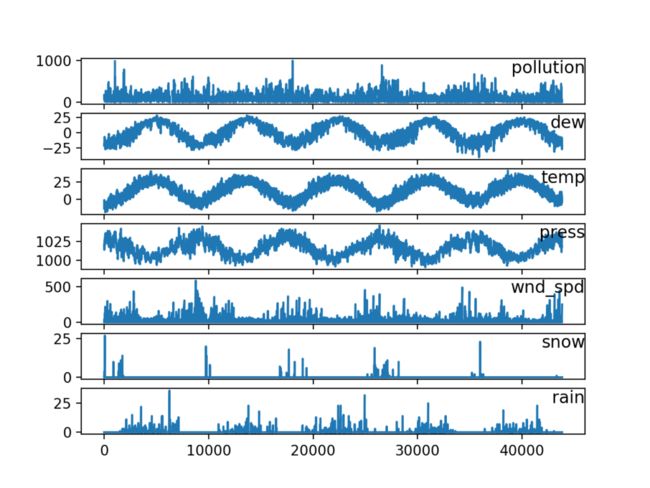
Running the example creates a plot with 7 subplots showing the 5 years of data for each variable.
Line Plots of Air Pollution Time Series
3. Multivariate LSTM Forecast Model
In this section, we will fit an LSTM to the problem.
LSTM Data Preparation
The first step is to prepare the pollution dataset for the LSTM.
This involves framing the dataset as a supervised learning problem and normalizing the input variables.
We will frame the supervised learning problem as predicting the pollution at the current hour (t) given the pollution measurement and weather conditions at the prior time step.
This formulation is straightforward and just for this demonstration. Some alternate formulations you could explore include:
- Predict the pollution for the next hour based on the weather conditions and pollution over the last 24 hours.
- Predict the pollution for the next hour as above and given the “expected” weather conditions for the next hour.
We can transform the dataset using the series_to_supervised() function developed in the blog post:
- How to Convert a Time Series to a Supervised Learning Problem in Python
First, the “pollution.csv” dataset is loaded. The wind speed feature is label encoded (integer encoded). This could further be one-hot encoded in the future if you are interested in exploring it.
Next, all features are normalized, then the dataset is transformed into a supervised learning problem. The weather variables for the hour to be predicted (t) are then removed.
The complete code listing is provided below.
# prepare data for lstm from pandas import read_csv from pandas import DataFrame from pandas import concat from sklearn.preprocessing import LabelEncoder from sklearn.preprocessing import MinMaxScaler # convert series to supervised learning def series_to_supervised(data, n_in=1, n_out=1, dropnan=True): n_vars = 1 if type(data) is list else data.shape[1] df = DataFrame(data) cols, names = list(), list() # input sequence (t-n, ... t-1) for i in range(n_in, 0, -1): cols.append(df.shift(i)) names += [('var%d(t-%d)' % (j+1, i)) for j in range(n_vars)] # forecast sequence (t, t+1, ... t+n) for i in range(0, n_out): cols.append(df.shift(-i)) if i == 0: names += [('var%d(t)' % (j+1)) for j in range(n_vars)] else: names += [('var%d(t+%d)' % (j+1, i)) for j in range(n_vars)] # put it all together agg = concat(cols, axis=1) agg.columns = names # drop rows with NaN values if dropnan: agg.dropna(inplace=True) return agg # load dataset dataset = read_csv('pollution.csv', header=0, index_col=0) values = dataset.values # integer encode direction encoder = LabelEncoder() values[:,4] = encoder.fit_transform(values[:,4]) # ensure all data is float values = values.astype('float32') # normalize features scaler = MinMaxScaler(feature_range=(0, 1)) scaled = scaler.fit_transform(values) # frame as supervised learning reframed = series_to_supervised(scaled, 1, 1) # drop columns we don't want to predict reframed.drop(reframed.columns[[9,10,11,12,13,14,15]], axis=1, inplace=True) print(reframed.head())
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 |
# prepare data for lstm from pandas import read_csv from pandas import DataFrame from pandas import concat from sklearn.preprocessing import LabelEncoder from sklearn.preprocessing import MinMaxScaler
# convert series to supervised learning def series_to_supervised(data, n_in=1, n_out=1, dropnan=True): n_vars = 1 if type(data) is list else data.shape[1] df = DataFrame(data) cols, names = list(), list() # input sequence (t-n, ... t-1) for i in range(n_in, 0, -1): cols.append(df.shift(i)) names += [('var%d(t-%d)' % (j+1, i)) for j in range(n_vars)] # forecast sequence (t, t+1, ... t+n) for i in range(0, n_out): cols.append(df.shift(-i)) if i == 0: names += [('var%d(t)' % (j+1)) for j in range(n_vars)] else: names += [('var%d(t+%d)' % (j+1, i)) for j in range(n_vars)] # put it all together agg = concat(cols, axis=1) agg.columns = names # drop rows with NaN values if dropnan: agg.dropna(inplace=True) return agg
# load dataset dataset = read_csv('pollution.csv', header=0, index_col=0) values = dataset.values # integer encode direction encoder = LabelEncoder() values[:,4] = encoder.fit_transform(values[:,4]) # ensure all data is float values = values.astype('float32') # normalize features scaler = MinMaxScaler(feature_range=(0, 1)) scaled = scaler.fit_transform(values) # frame as supervised learning reframed = series_to_supervised(scaled, 1, 1) # drop columns we don't want to predict reframed.drop(reframed.columns[[9,10,11,12,13,14,15]], axis=1, inplace=True) print(reframed.head()) |
Running the example prints the first 5 rows of the transformed dataset. We can see the 8 input variables (input series) and the 1 output variable (pollution level at the current hour).
var1(t-1) var2(t-1) var3(t-1) var4(t-1) var5(t-1) var6(t-1) \ 1 0.129779 0.352941 0.245902 0.527273 0.666667 0.002290 2 0.148893 0.367647 0.245902 0.527273 0.666667 0.003811 3 0.159960 0.426471 0.229508 0.545454 0.666667 0.005332 4 0.182093 0.485294 0.229508 0.563637 0.666667 0.008391 5 0.138833 0.485294 0.229508 0.563637 0.666667 0.009912 var7(t-1) var8(t-1) var1(t) 1 0.000000 0.0 0.148893 2 0.000000 0.0 0.159960 3 0.000000 0.0 0.182093 4 0.037037 0.0 0.138833 5 0.074074 0.0 0.109658
| 1 2 3 4 5 6 7 8 9 10 11 12 13 |
var1(t-1) var2(t-1) var3(t-1) var4(t-1) var5(t-1) var6(t-1) \ 1 0.129779 0.352941 0.245902 0.527273 0.666667 0.002290 2 0.148893 0.367647 0.245902 0.527273 0.666667 0.003811 3 0.159960 0.426471 0.229508 0.545454 0.666667 0.005332 4 0.182093 0.485294 0.229508 0.563637 0.666667 0.008391 5 0.138833 0.485294 0.229508 0.563637 0.666667 0.009912 var7(t-1) var8(t-1) var1(t) 1 0.000000 0.0 0.148893 2 0.000000 0.0 0.159960 3 0.000000 0.0 0.182093 4 0.037037 0.0 0.138833 5 0.074074 0.0 0.109658 |
This data preparation is simple and there is more we could explore. Some ideas you could look at include:
- One-hot encoding wind direction.
- Making all series stationary with differencing and seasonal adjustment.
- Providing more than 1 hour of input time steps.
This last point is perhaps the most important given the use of Backpropagation through time by LSTMs when learning sequence prediction problems.
Define and Fit Model
In this section, we will fit an LSTM on the multivariate input data.
First, we must split the prepared dataset into train and test sets. To speed up the training of the model for this demonstration, we will only fit the model on the first year of data, then evaluate it on the remaining 4 years of data. If you have time, consider exploring the inverted version of this test harness.
The example below splits the dataset into train and test sets, then splits the train and test sets into input and output variables. Finally, the inputs (X) are reshaped into the 3D format expected by LSTMs, namely [samples, timesteps, features].
... # split into train and test sets values = reframed.values n_train_hours = 365 * 24 train = values[:n_train_hours, :] test = values[n_train_hours:, :] # split into input and outputs train_X, train_y = train[:, :-1], train[:, -1] test_X, test_y = test[:, :-1], test[:, -1] # reshape input to be 3D [samples, timesteps, features] train_X = train_X.reshape((train_X.shape[0], 1, train_X.shape[1])) test_X = test_X.reshape((test_X.shape[0], 1, test_X.shape[1])) print(train_X.shape, train_y.shape, test_X.shape, test_y.shape)
| 1 2 3 4 5 6 7 8 9 10 11 12 13 |
... # split into train and test sets values = reframed.values n_train_hours = 365 * 24 train = values[:n_train_hours, :] test = values[n_train_hours:, :] # split into input and outputs train_X, train_y = train[:, :-1], train[:, -1] test_X, test_y = test[:, :-1], test[:, -1] # reshape input to be 3D [samples, timesteps, features] train_X = train_X.reshape((train_X.shape[0], 1, train_X.shape[1])) test_X = test_X.reshape((test_X.shape[0], 1, test_X.shape[1])) print(train_X.shape, train_y.shape, test_X.shape, test_y.shape) |
Running this example prints the shape of the train and test input and output sets with about 9K hours of data for training and about 35K hours for testing.
(8760, 1, 8) (8760,) (35039, 1, 8) (35039,)
| 1 |
(8760, 1, 8) (8760,) (35039, 1, 8) (35039,) |
Now we can define and fit our LSTM model.
We will define the LSTM with 50 neurons in the first hidden layer and 1 neuron in the output layer for predicting pollution. The input shape will be 1 time step with 8 features.
We will use the Mean Absolute Error (MAE) loss function and the efficient Adam version of stochastic gradient descent.
The model will be fit for 50 training epochs with a batch size of 72. Remember that the internal state of the LSTM in Keras is reset at the end of each batch, so an internal state that is a function of a number of days may be helpful (try testing this).
Finally, we keep track of both the training and test loss during training by setting the validation_data argument in the fit() function. At the end of the run both the training and test loss are plotted.
... # design network model = Sequential() model.add(LSTM(50, input_shape=(train_X.shape[1], train_X.shape[2]))) model.add(Dense(1)) model.compile(loss='mae', optimizer='adam') # fit network history = model.fit(train_X, train_y, epochs=50, batch_size=72, validation_data=(test_X, test_y), verbose=2, shuffle=False) # plot history pyplot.plot(history.history['loss'], label='train') pyplot.plot(history.history['val_loss'], label='test') pyplot.legend() pyplot.show()
| 1 2 3 4 5 6 7 8 9 10 11 12 13 |
... # design network model = Sequential() model.add(LSTM(50, input_shape=(train_X.shape[1], train_X.shape[2]))) model.add(Dense(1)) model.compile(loss='mae', optimizer='adam') # fit network history = model.fit(train_X, train_y, epochs=50, batch_size=72, validation_data=(test_X, test_y), verbose=2, shuffle=False) # plot history pyplot.plot(history.history['loss'], label='train') pyplot.plot(history.history['val_loss'], label='test') pyplot.legend() pyplot.show() |
Evaluate Model
After the model is fit, we can forecast for the entire test dataset.
We combine the forecast with the test dataset and invert the scaling. We also invert scaling on the test dataset with the expected pollution numbers.
With forecasts and actual values in their original scale, we can then calculate an error score for the model. In this case, we calculate the Root Mean Squared Error (RMSE) that gives error in the same units as the variable itself.
... # make a prediction yhat = model.predict(test_X) test_X = test_X.reshape((test_X.shape[0], test_X.shape[2])) # invert scaling for forecast inv_yhat = concatenate((yhat, test_X[:, 1:]), axis=1) inv_yhat = scaler.inverse_transform(inv_yhat) inv_yhat = inv_yhat[:,0] # invert scaling for actual test_y = test_y.reshape((len(test_y), 1)) inv_y = concatenate((test_y, test_X[:, 1:]), axis=1) inv_y = scaler.inverse_transform(inv_y) inv_y = inv_y[:,0] # calculate RMSE rmse = sqrt(mean_squared_error(inv_y, inv_yhat)) print('Test RMSE: %.3f' % rmse)
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
... # make a prediction yhat = model.predict(test_X) test_X = test_X.reshape((test_X.shape[0], test_X.shape[2])) # invert scaling for forecast inv_yhat = concatenate((yhat, test_X[:, 1:]), axis=1) inv_yhat = scaler.inverse_transform(inv_yhat) inv_yhat = inv_yhat[:,0] # invert scaling for actual test_y = test_y.reshape((len(test_y), 1)) inv_y = concatenate((test_y, test_X[:, 1:]), axis=1) inv_y = scaler.inverse_transform(inv_y) inv_y = inv_y[:,0] # calculate RMSE rmse = sqrt(mean_squared_error(inv_y, inv_yhat)) print('Test RMSE: %.3f' % rmse) |
Complete Example
The complete example is listed below.
NOTE: This example assumes you have prepared the data correctly, e.g. converted the downloaded “raw.csv” to the prepared “pollution.csv“. See the first part of this tutorial.
from math import sqrt from numpy import concatenate from matplotlib import pyplot from pandas import read_csv from pandas import DataFrame from pandas import concat from sklearn.preprocessing import MinMaxScaler from sklearn.preprocessing import LabelEncoder from sklearn.metrics import mean_squared_error from keras.models import Sequential from keras.layers import Dense from keras.layers import LSTM # convert series to supervised learning def series_to_supervised(data, n_in=1, n_out=1, dropnan=True): n_vars = 1 if type(data) is list else data.shape[1] df = DataFrame(data) cols, names = list(), list() # input sequence (t-n, ... t-1) for i in range(n_in, 0, -1): cols.append(df.shift(i)) names += [('var%d(t-%d)' % (j+1, i)) for j in range(n_vars)] # forecast sequence (t, t+1, ... t+n) for i in range(0, n_out): cols.append(df.shift(-i)) if i == 0: names += [('var%d(t)' % (j+1)) for j in range(n_vars)] else: names += [('var%d(t+%d)' % (j+1, i)) for j in range(n_vars)] # put it all together agg = concat(cols, axis=1) agg.columns = names # drop rows with NaN values if dropnan: agg.dropna(inplace=True) return agg # load dataset dataset = read_csv('pollution.csv', header=0, index_col=0) values = dataset.values # integer encode direction encoder = LabelEncoder() values[:,4] = encoder.fit_transform(values[:,4]) # ensure all data is float values = values.astype('float32') # normalize features scaler = MinMaxScaler(feature_range=(0, 1)) scaled = scaler.fit_transform(values) # frame as supervised learning reframed = series_to_supervised(scaled, 1, 1) # drop columns we don't want to predict reframed.drop(reframed.columns[[9,10,11,12,13,14,15]], axis=1, inplace=True) print(reframed.head()) # split into train and test sets values = reframed.values n_train_hours = 365 * 24 train = values[:n_train_hours, :] test = values[n_train_hours:, :] # split into input and outputs train_X, train_y = train[:, :-1], train[:, -1] test_X, test_y = test[:, :-1], test[:, -1] # reshape input to be 3D [samples, timesteps, features] train_X = train_X.reshape((train_X.shape[0], 1, train_X.shape[1])) test_X = test_X.reshape((test_X.shape[0], 1, test_X.shape[1])) print(train_X.shape, train_y.shape, test_X.shape, test_y.shape) # design network model = Sequential() model.add(LSTM(50, input_shape=(train_X.shape[1], train_X.shape[2]))) model.add(Dense(1)) model.compile(loss='mae', optimizer='adam') # fit network history = model.fit(train_X, train_y, epochs=50, batch_size=72, validation_data=(test_X, test_y), verbose=2, shuffle=False) # plot history pyplot.plot(history.history['loss'], label='train') pyplot.plot(history.history['val_loss'], label='test') pyplot.legend() pyplot.show() # make a prediction yhat = model.predict(test_X) test_X = test_X.reshape((test_X.shape[0], test_X.shape[2])) # invert scaling for forecast inv_yhat = concatenate((yhat, test_X[:, 1:]), axis=1) inv_yhat = scaler.inverse_transform(inv_yhat) inv_yhat = inv_yhat[:,0] # invert scaling for actual test_y = test_y.reshape((len(test_y), 1)) inv_y = concatenate((test_y, test_X[:, 1:]), axis=1) inv_y = scaler.inverse_transform(inv_y) inv_y = inv_y[:,0] # calculate RMSE rmse = sqrt(mean_squared_error(inv_y, inv_yhat)) print('Test RMSE: %.3f' % rmse)
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 |
from math import sqrt from numpy import concatenate from matplotlib import pyplot from pandas import read_csv from pandas import DataFrame from pandas import concat from sklearn.preprocessing import MinMaxScaler from sklearn.preprocessing import LabelEncoder from sklearn.metrics import mean_squared_error from keras.models import Sequential from keras.layers import Dense from keras.layers import LSTM # convert series to supervised learning def series_to_supervised(data, n_in=1, n_out=1, dropnan=True): n_vars = 1 if type(data) is list else data.shape[1] df = DataFrame(data) cols, names = list(), list() # input sequence (t-n, ... t-1) for i in range(n_in, 0, -1): cols.append(df.shift(i)) names += [('var%d(t-%d)' % (j+1, i)) for j in range(n_vars)] # forecast sequence (t, t+1, ... t+n) for i in range(0, n_out): cols.append(df.shift(-i)) if i == 0: names += [('var%d(t)' % (j+1)) for j in range(n_vars)] else: names += [('var%d(t+%d)' % (j+1, i)) for j in range(n_vars)] # put it all together agg = concat(cols, axis=1) agg.columns = names # drop rows with NaN values if dropnan: agg.dropna(inplace=True) return agg # load dataset dataset = read_csv('pollution.csv', header=0, index_col=0) values = dataset.values # integer encode direction encoder = LabelEncoder() values[:,4] = encoder.fit_transform(values[:,4]) # ensure all data is float values = values.astype('float32') # normalize features scaler = MinMaxScaler(feature_range=(0, 1)) scaled = scaler.fit_transform(values) # frame as supervised learning reframed = series_to_supervised(scaled, 1, 1) # drop columns we don't want to predict reframed.drop(reframed.columns[[9,10,11,12,13,14,15]], axis=1, inplace=True) print(reframed.head()) # split into train and test sets values = reframed.values n_train_hours = 365 * 24 train = values[:n_train_hours, :] test = values[n_train_hours:, :] # split into input and outputs train_X, train_y = train[:, :-1], train[:, -1] test_X, test_y = test[:, :-1], test[:, -1] # reshape input to be 3D [samples, timesteps, features] train_X = train_X.reshape((train_X.shape[0], 1, train_X.shape[1])) test_X = test_X.reshape((test_X.shape[0], 1, test_X.shape[1])) print(train_X.shape, train_y.shape, test_X.shape, test_y.shape) # design network model = Sequential() model.add(LSTM(50, input_shape=(train_X.shape[1], train_X.shape[2]))) model.add(Dense(1)) model.compile(loss='mae', optimizer='adam') # fit network history = model.fit(train_X, train_y, epochs=50, batch_size=72, validation_data=(test_X, test_y), verbose=2, shuffle=False) # plot history pyplot.plot(history.history['loss'], label='train') pyplot.plot(history.history['val_loss'], label='test') pyplot.legend() pyplot.show() # make a prediction yhat = model.predict(test_X) test_X = test_X.reshape((test_X.shape[0], test_X.shape[2])) # invert scaling for forecast inv_yhat = concatenate((yhat, test_X[:, 1:]), axis=1) inv_yhat = scaler.inverse_transform(inv_yhat) inv_yhat = inv_yhat[:,0] # invert scaling for actual test_y = test_y.reshape((len(test_y), 1)) inv_y = concatenate((test_y, test_X[:, 1:]), axis=1) inv_y = scaler.inverse_transform(inv_y) inv_y = inv_y[:,0] # calculate RMSE rmse = sqrt(mean_squared_error(inv_y, inv_yhat)) print('Test RMSE: %.3f' % rmse) |
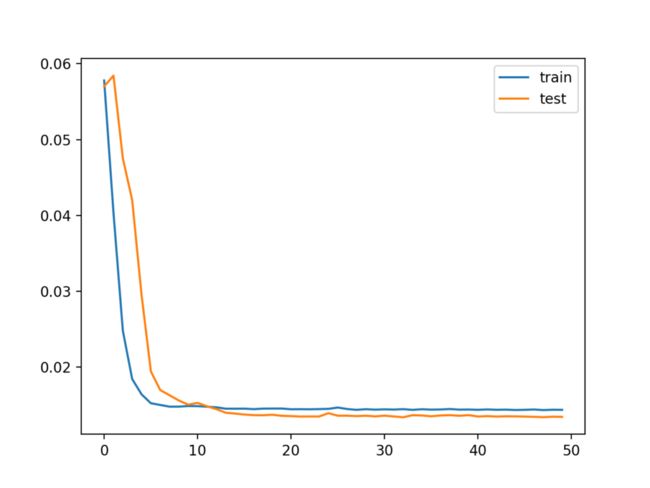
Running the example first creates a plot showing the train and test loss during training.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
Interestingly, we can see that test loss drops below training loss. The model may be overfitting the training data. Measuring and plotting RMSE during training may shed more light on this.
Line Plot of Train and Test Loss from the Multivariate LSTM During Training
The Train and test loss are printed at the end of each training epoch. At the end of the run, the final RMSE of the model on the test dataset is printed.
We can see that the model achieves a respectable RMSE of 26.496, which is lower than an RMSE of 30 found with a persistence model.
... Epoch 46/50 0s - loss: 0.0143 - val_loss: 0.0133 Epoch 47/50 0s - loss: 0.0143 - val_loss: 0.0133 Epoch 48/50 0s - loss: 0.0144 - val_loss: 0.0133 Epoch 49/50 0s - loss: 0.0143 - val_loss: 0.0133 Epoch 50/50 0s - loss: 0.0144 - val_loss: 0.0133 Test RMSE: 26.496
| 1 2 3 4 5 6 7 8 9 10 11 12 |
... Epoch 46/50 0s - loss: 0.0143 - val_loss: 0.0133 Epoch 47/50 0s - loss: 0.0143 - val_loss: 0.0133 Epoch 48/50 0s - loss: 0.0144 - val_loss: 0.0133 Epoch 49/50 0s - loss: 0.0143 - val_loss: 0.0133 Epoch 50/50 0s - loss: 0.0144 - val_loss: 0.0133 Test RMSE: 26.496 |
This model is not tuned. Can you do better?
Let me know your problem framing, model configuration, and RMSE in the comments below.
Train On Multiple Lag Timesteps Example
There have been many requests for advice on how to adapt the above example to train the model on multiple previous time steps.
I had tried this and a myriad of other configurations when writing the original post and decided not to include them because they did not lift model skill.
Nevertheless, I have included this example below as reference template that you could adapt for your own problems.
The changes needed to train the model on multiple previous time steps are quite minimal, as follows:
First, you must frame the problem suitably when calling series_to_supervised(). We will use 3 hours of data as input. Also note, we no longer explictly drop the columns from all of the other fields at ob(t).
... # specify the number of lag hours n_hours = 3 n_features = 8 # frame as supervised learning reframed = series_to_supervised(scaled, n_hours, 1)
| 1 2 3 4 5 6 |
... # specify the number of lag hours n_hours = 3 n_features = 8 # frame as supervised learning reframed = series_to_supervised(scaled, n_hours, 1) |
Next, we need to be more careful in specifying the column for input and output.
We have 3 * 8 + 8 columns in our framed dataset. We will take 3 * 8 or 24 columns as input for the obs of all features across the previous 3 hours. We will take just the pollution variable as output at the following hour, as follows:
... # split into input and outputs n_obs = n_hours * n_features train_X, train_y = train[:, :n_obs], train[:, -n_features] test_X, test_y = test[:, :n_obs], test[:, -n_features] print(train_X.shape, len(train_X), train_y.shape)
| 1 2 3 4 5 6 |
... # split into input and outputs n_obs = n_hours * n_features train_X, train_y = train[:, :n_obs], train[:, -n_features] test_X, test_y = test[:, :n_obs], test[:, -n_features] print(train_X.shape, len(train_X), train_y.shape) |
Next, we can reshape our input data correctly to reflect the time steps and features.
... # reshape input to be 3D [samples, timesteps, features] train_X = train_X.reshape((train_X.shape[0], n_hours, n_features)) test_X = test_X.reshape((test_X.shape[0], n_hours, n_features))
| 1 2 3 4 |
... # reshape input to be 3D [samples, timesteps, features] train_X = train_X.reshape((train_X.shape[0], n_hours, n_features)) test_X = test_X.reshape((test_X.shape[0], n_hours, n_features)) |
Fitting the model is the same.
The only other small change is in how to evaluate the model. Specifically, in how we reconstruct the rows with 8 columns suitable for reversing the scaling operation to get the y and yhat back into the original scale so that we can calculate the RMSE.
The gist of the change is that we concatenate the y or yhat column with the last 7 features of the test dataset in order to inverse the scaling, as follows:
... # invert scaling for forecast inv_yhat = concatenate((yhat, test_X[:, -7:]), axis=1) inv_yhat = scaler.inverse_transform(inv_yhat) inv_yhat = inv_yhat[:,0] # invert scaling for actual test_y = test_y.reshape((len(test_y), 1)) inv_y = concatenate((test_y, test_X[:, -7:]), axis=1) inv_y = scaler.inverse_transform(inv_y) inv_y = inv_y[:,0]
| 1 2 3 4 5 6 7 8 9 10 |
... # invert scaling for forecast inv_yhat = concatenate((yhat, test_X[:, -7:]), axis=1) inv_yhat = scaler.inverse_transform(inv_yhat) inv_yhat = inv_yhat[:,0] # invert scaling for actual test_y = test_y.reshape((len(test_y), 1)) inv_y = concatenate((test_y, test_X[:, -7:]), axis=1) inv_y = scaler.inverse_transform(inv_y) inv_y = inv_y[:,0] |
We can tie all of these modifications to the above example together. The complete example of multvariate time series forecasting with multiple lag inputs is listed below:
from math import sqrt from numpy import concatenate from matplotlib import pyplot from pandas import read_csv from pandas import DataFrame from pandas import concat from sklearn.preprocessing import MinMaxScaler from sklearn.preprocessing import LabelEncoder from sklearn.metrics import mean_squared_error from keras.models import Sequential from keras.layers import Dense from keras.layers import LSTM # convert series to supervised learning def series_to_supervised(data, n_in=1, n_out=1, dropnan=True): n_vars = 1 if type(data) is list else data.shape[1] df = DataFrame(data) cols, names = list(), list() # input sequence (t-n, ... t-1) for i in range(n_in, 0, -1): cols.append(df.shift(i)) names += [('var%d(t-%d)' % (j+1, i)) for j in range(n_vars)] # forecast sequence (t, t+1, ... t+n) for i in range(0, n_out): cols.append(df.shift(-i)) if i == 0: names += [('var%d(t)' % (j+1)) for j in range(n_vars)] else: names += [('var%d(t+%d)' % (j+1, i)) for j in range(n_vars)] # put it all together agg = concat(cols, axis=1) agg.columns = names # drop rows with NaN values if dropnan: agg.dropna(inplace=True) return agg # load dataset dataset = read_csv('pollution.csv', header=0, index_col=0) values = dataset.values # integer encode direction encoder = LabelEncoder() values[:,4] = encoder.fit_transform(values[:,4]) # ensure all data is float values = values.astype('float32') # normalize features scaler = MinMaxScaler(feature_range=(0, 1)) scaled = scaler.fit_transform(values) # specify the number of lag hours n_hours = 3 n_features = 8 # frame as supervised learning reframed = series_to_supervised(scaled, n_hours, 1) print(reframed.shape) # split into train and test sets values = reframed.values n_train_hours = 365 * 24 train = values[:n_train_hours, :] test = values[n_train_hours:, :] # split into input and outputs n_obs = n_hours * n_features train_X, train_y = train[:, :n_obs], train[:, -n_features] test_X, test_y = test[:, :n_obs], test[:, -n_features] print(train_X.shape, len(train_X), train_y.shape) # reshape input to be 3D [samples, timesteps, features] train_X = train_X.reshape((train_X.shape[0], n_hours, n_features)) test_X = test_X.reshape((test_X.shape[0], n_hours, n_features)) print(train_X.shape, train_y.shape, test_X.shape, test_y.shape) # design network model = Sequential() model.add(LSTM(50, input_shape=(train_X.shape[1], train_X.shape[2]))) model.add(Dense(1)) model.compile(loss='mae', optimizer='adam') # fit network history = model.fit(train_X, train_y, epochs=50, batch_size=72, validation_data=(test_X, test_y), verbose=2, shuffle=False) # plot history pyplot.plot(history.history['loss'], label='train') pyplot.plot(history.history['val_loss'], label='test') pyplot.legend() pyplot.show() # make a prediction yhat = model.predict(test_X) test_X = test_X.reshape((test_X.shape[0], n_hours*n_features)) # invert scaling for forecast inv_yhat = concatenate((yhat, test_X[:, -7:]), axis=1) inv_yhat = scaler.inverse_transform(inv_yhat) inv_yhat = inv_yhat[:,0] # invert scaling for actual test_y = test_y.reshape((len(test_y), 1)) inv_y = concatenate((test_y, test_X[:, -7:]), axis=1) inv_y = scaler.inverse_transform(inv_y) inv_y = inv_y[:,0] # calculate RMSE rmse = sqrt(mean_squared_error(inv_y, inv_yhat)) print('Test RMSE: %.3f' % rmse)
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 |
from math import sqrt from numpy import concatenate from matplotlib import pyplot from pandas import read_csv from pandas import DataFrame from pandas import concat from sklearn.preprocessing import MinMaxScaler from sklearn.preprocessing import LabelEncoder from sklearn.metrics import mean_squared_error from keras.models import Sequential from keras.layers import Dense from keras.layers import LSTM
# convert series to supervised learning def series_to_supervised(data, n_in=1, n_out=1, dropnan=True): n_vars = 1 if type(data) is list else data.shape[1] df = DataFrame(data) cols, names = list(), list() # input sequence (t-n, ... t-1) for i in range(n_in, 0, -1): cols.append(df.shift(i)) names += [('var%d(t-%d)' % (j+1, i)) for j in range(n_vars)] # forecast sequence (t, t+1, ... t+n) for i in range(0, n_out): cols.append(df.shift(-i)) if i == 0: names += [('var%d(t)' % (j+1)) for j in range(n_vars)] else: names += [('var%d(t+%d)' % (j+1, i)) for j in range(n_vars)] # put it all together agg = concat(cols, axis=1) agg.columns = names # drop rows with NaN values if dropnan: agg.dropna(inplace=True) return agg
# load dataset dataset = read_csv('pollution.csv', header=0, index_col=0) values = dataset.values # integer encode direction encoder = LabelEncoder() values[:,4] = encoder.fit_transform(values[:,4]) # ensure all data is float values = values.astype('float32') # normalize features scaler = MinMaxScaler(feature_range=(0, 1)) scaled = scaler.fit_transform(values) # specify the number of lag hours n_hours = 3 n_features = 8 # frame as supervised learning reframed = series_to_supervised(scaled, n_hours, 1) print(reframed.shape)
# split into train and test sets values = reframed.values n_train_hours = 365 * 24 train = values[:n_train_hours, :] test = values[n_train_hours:, :] # split into input and outputs n_obs = n_hours * n_features train_X, train_y = train[:, :n_obs], train[:, -n_features] test_X, test_y = test[:, :n_obs], test[:, -n_features] print(train_X.shape, len(train_X), train_y.shape) # reshape input to be 3D [samples, timesteps, features] train_X = train_X.reshape((train_X.shape[0], n_hours, n_features)) test_X = test_X.reshape((test_X.shape[0], n_hours, n_features)) print(train_X.shape, train_y.shape, test_X.shape, test_y.shape)
# design network model = Sequential() model.add(LSTM(50, input_shape=(train_X.shape[1], train_X.shape[2]))) model.add(Dense(1)) model.compile(loss='mae', optimizer='adam') # fit network history = model.fit(train_X, train_y, epochs=50, batch_size=72, validation_data=(test_X, test_y), verbose=2, shuffle=False) # plot history pyplot.plot(history.history['loss'], label='train') pyplot.plot(history.history['val_loss'], label='test') pyplot.legend() pyplot.show()
# make a prediction yhat = model.predict(test_X) test_X = test_X.reshape((test_X.shape[0], n_hours*n_features)) # invert scaling for forecast inv_yhat = concatenate((yhat, test_X[:, -7:]), axis=1) inv_yhat = scaler.inverse_transform(inv_yhat) inv_yhat = inv_yhat[:,0] # invert scaling for actual test_y = test_y.reshape((len(test_y), 1)) inv_y = concatenate((test_y, test_X[:, -7:]), axis=1) inv_y = scaler.inverse_transform(inv_y) inv_y = inv_y[:,0] # calculate RMSE rmse = sqrt(mean_squared_error(inv_y, inv_yhat)) print('Test RMSE: %.3f' % rmse) |
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
The model is fit as before in a minute or two.
... Epoch 45/50 1s - loss: 0.0143 - val_loss: 0.0154 Epoch 46/50 1s - loss: 0.0143 - val_loss: 0.0148 Epoch 47/50 1s - loss: 0.0143 - val_loss: 0.0152 Epoch 48/50 1s - loss: 0.0143 - val_loss: 0.0151 Epoch 49/50 1s - loss: 0.0143 - val_loss: 0.0152 Epoch 50/50 1s - loss: 0.0144 - val_loss: 0.0149
| 1 2 3 4 5 6 7 8 9 10 11 12 13 |
... Epoch 45/50 1s - loss: 0.0143 - val_loss: 0.0154 Epoch 46/50 1s - loss: 0.0143 - val_loss: 0.0148 Epoch 47/50 1s - loss: 0.0143 - val_loss: 0.0152 Epoch 48/50 1s - loss: 0.0143 - val_loss: 0.0151 Epoch 49/50 1s - loss: 0.0143 - val_loss: 0.0152 Epoch 50/50 1s - loss: 0.0144 - val_loss: 0.0149 |
A plot of train and test loss over the epochs is plotted.
Plot of Loss on the Train and Test Datasets
Finally, the Test RMSE is printed, not really showing any advantage in skill, at least on this problem.
Test RMSE: 27.177
| 1 |
Test RMSE: 27.177 |
I would add that the LSTM does not appear to be suitable for autoregression type problems and that you may be better off exploring an MLP with a large window.
I hope this example helps you with your own time series forecasting experiments.
Further Reading
This section provides more resources on the topic if you are looking go deeper.
- Beijing PM2.5 Data Set on the UCI Machine Learning Repository
- The 5 Step Life-Cycle for Long Short-Term Memory Models in Keras
- Time Series Forecasting with the Long Short-Term Memory Network in Python
- Multi-step Time Series Forecasting with Long Short-Term Memory Networks in Python
Summary
In this tutorial, you discovered how to fit an LSTM to a multivariate time series forecasting problem.
Specifically, you learned:
- How to transform a raw dataset into something we can use for time series forecasting.
- How to prepare data and fit an LSTM for a multivariate time series forecasting problem.
- How to make a forecast and rescale the result back into the original units.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.
1. Air Pollution Forecasting
In this tutorial, we are going to use the Air Quality dataset.
This is a dataset that reports on the weather and the level of pollution each hour for five years at the US embassy in Beijing, China.
The data includes the date-time, the pollution called PM2.5 concentration, and the weather information including dew point, temperature, pressure, wind direction, wind speed and the cumulative number of hours of snow and rain. The complete feature list in the raw data is as follows:
- No: row number
- year: year of data in this row
- month: month of data in this row
- day: day of data in this row
- hour: hour of data in this row
- pm2.5: PM2.5 concentration
- DEWP: Dew Point
- TEMP: Temperature
- PRES: Pressure
- cbwd: Combined wind direction
- Iws: Cumulated wind speed
- Is: Cumulated hours of snow
- Ir: Cumulated hours of rain
We can use this data and frame a forecasting problem where, given the weather conditions and pollution for prior hours, we forecast the pollution at the next hour.
This dataset can be used to frame other forecasting problems.
Do you have good ideas? Let me know in the comments below.
You can download the dataset from the UCI Machine Learning Repository.
Update, I have mirrored the dataset here because UCI has become unreliable:
- Beijing PM2.5 Data Set
Download the dataset and place it in your current working directory with the filename “raw.csv“.
2. Basic Data Preparation
The data is not ready to use. We must prepare it first.
Below are the first few rows of the raw dataset.
No,year,month,day,hour,pm2.5,DEWP,TEMP,PRES,cbwd,Iws,Is,Ir 1,2010,1,1,0,NA,-21,-11,1021,NW,1.79,0,0 2,2010,1,1,1,NA,-21,-12,1020,NW,4.92,0,0 3,2010,1,1,2,NA,-21,-11,1019,NW,6.71,0,0 4,2010,1,1,3,NA,-21,-14,1019,NW,9.84,0,0 5,2010,1,1,4,NA,-20,-12,1018,NW,12.97,0,0
| 1 2 3 4 5 6 |
No,year,month,day,hour,pm2.5,DEWP,TEMP,PRES,cbwd,Iws,Is,Ir 1,2010,1,1,0,NA,-21,-11,1021,NW,1.79,0,0 2,2010,1,1,1,NA,-21,-12,1020,NW,4.92,0,0 3,2010,1,1,2,NA,-21,-11,1019,NW,6.71,0,0 4,2010,1,1,3,NA,-21,-14,1019,NW,9.84,0,0 5,2010,1,1,4,NA,-20,-12,1018,NW,12.97,0,0 |
The first step is to consolidate the date-time information into a single date-time so that we can use it as an index in Pandas.
A quick check reveals NA values for pm2.5 for the first 24 hours. We will, therefore, need to remove the first row of data. There are also a few scattered “NA” values later in the dataset; we can mark them with 0 values for now.
The script below loads the raw dataset and parses the date-time information as the Pandas DataFrame index. The “No” column is dropped and then clearer names are specified for each column. Finally, the NA values are replaced with “0” values and the first 24 hours are removed.
The “No” column is dropped and then clearer names are specified for each column. Finally, the NA values are replaced with “0” values and the first 24 hours are removed.
from pandas import read_csv from datetime import datetime # load data def parse(x): return datetime.strptime(x, '%Y %m %d %H') dataset = read_csv('raw.csv', parse_dates = [['year', 'month', 'day', 'hour']], index_col=0, date_parser=parse) dataset.drop('No', axis=1, inplace=True) # manually specify column names dataset.columns = ['pollution', 'dew', 'temp', 'press', 'wnd_dir', 'wnd_spd', 'snow', 'rain'] dataset.index.name = 'date' # mark all NA values with 0 dataset['pollution'].fillna(0, inplace=True) # drop the first 24 hours dataset = dataset[24:] # summarize first 5 rows print(dataset.head(5)) # save to file dataset.to_csv('pollution.csv')
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
from pandas import read_csv from datetime import datetime # load data def parse(x): return datetime.strptime(x, '%Y %m %d %H') dataset = read_csv('raw.csv', parse_dates = [['year', 'month', 'day', 'hour']], index_col=0, date_parser=parse) dataset.drop('No', axis=1, inplace=True) # manually specify column names dataset.columns = ['pollution', 'dew', 'temp', 'press', 'wnd_dir', 'wnd_spd', 'snow', 'rain'] dataset.index.name = 'date' # mark all NA values with 0 dataset['pollution'].fillna(0, inplace=True) # drop the first 24 hours dataset = dataset[24:] # summarize first 5 rows print(dataset.head(5)) # save to file dataset.to_csv('pollution.csv') |
Running the example prints the first 5 rows of the transformed dataset and saves the dataset to “pollution.csv“.
pollution dew temp press wnd_dir wnd_spd snow rain date 2010-01-02 00:00:00 129.0 -16 -4.0 1020.0 SE 1.79 0 0 2010-01-02 01:00:00 148.0 -15 -4.0 1020.0 SE 2.68 0 0 2010-01-02 02:00:00 159.0 -11 -5.0 1021.0 SE 3.57 0 0 2010-01-02 03:00:00 181.0 -7 -5.0 1022.0 SE 5.36 1 0 2010-01-02 04:00:00 138.0 -7 -5.0 1022.0 SE 6.25 2 0
| 1 2 3 4 5 6 7 |
pollution dew temp press wnd_dir wnd_spd snow rain date 2010-01-02 00:00:00 129.0 -16 -4.0 1020.0 SE 1.79 0 0 2010-01-02 01:00:00 148.0 -15 -4.0 1020.0 SE 2.68 0 0 2010-01-02 02:00:00 159.0 -11 -5.0 1021.0 SE 3.57 0 0 2010-01-02 03:00:00 181.0 -7 -5.0 1022.0 SE 5.36 1 0 2010-01-02 04:00:00 138.0 -7 -5.0 1022.0 SE 6.25 2 0 |
Now that we have the data in an easy-to-use form, we can create a quick plot of each series and see what we have.
The code below loads the new “pollution.csv” file and plots each series as a separate subplot, except wind speed dir, which is categorical.
from pandas import read_csv from matplotlib import pyplot # load dataset dataset = read_csv('pollution.csv', header=0, index_col=0) values = dataset.values # specify columns to plot groups = [0, 1, 2, 3, 5, 6, 7] i = 1 # plot each column pyplot.figure() for group in groups: pyplot.subplot(len(groups), 1, i) pyplot.plot(values[:, group]) pyplot.title(dataset.columns[group], y=0.5, loc='right') i += 1 pyplot.show()
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
from pandas import read_csv from matplotlib import pyplot # load dataset dataset = read_csv('pollution.csv', header=0, index_col=0) values = dataset.values # specify columns to plot groups = [0, 1, 2, 3, 5, 6, 7] i = 1 # plot each column pyplot.figure() for group in groups: pyplot.subplot(len(groups), 1, i) pyplot.plot(values[:, group]) pyplot.title(dataset.columns[group], y=0.5, loc='right') i += 1 pyplot.show() |
Running the example creates a plot with 7 subplots showing the 5 years of data for each variable.
Line Plots of Air Pollution Time Series
3. Multivariate LSTM Forecast Model
In this section, we will fit an LSTM to the problem.
LSTM Data Preparation
The first step is to prepare the pollution dataset for the LSTM.
This involves framing the dataset as a supervised learning problem and normalizing the input variables.
We will frame the supervised learning problem as predicting the pollution at the current hour (t) given the pollution measurement and weather conditions at the prior time step.
This formulation is straightforward and just for this demonstration. Some alternate formulations you could explore include:
- Predict the pollution for the next hour based on the weather conditions and pollution over the last 24 hours.
- Predict the pollution for the next hour as above and given the “expected” weather conditions for the next hour.
We can transform the dataset using the series_to_supervised() function developed in the blog post:
- How to Convert a Time Series to a Supervised Learning Problem in Python
First, the “pollution.csv” dataset is loaded. The wind speed feature is label encoded (integer encoded). This could further be one-hot encoded in the future if you are interested in exploring it.
Next, all features are normalized, then the dataset is transformed into a supervised learning problem. The weather variables for the hour to be predicted (t) are then removed.
The complete code listing is provided below.
# prepare data for lstm from pandas import read_csv from pandas import DataFrame from pandas import concat from sklearn.preprocessing import LabelEncoder from sklearn.preprocessing import MinMaxScaler # convert series to supervised learning def series_to_supervised(data, n_in=1, n_out=1, dropnan=True): n_vars = 1 if type(data) is list else data.shape[1] df = DataFrame(data) cols, names = list(), list() # input sequence (t-n, ... t-1) for i in range(n_in, 0, -1): cols.append(df.shift(i)) names += [('var%d(t-%d)' % (j+1, i)) for j in range(n_vars)] # forecast sequence (t, t+1, ... t+n) for i in range(0, n_out): cols.append(df.shift(-i)) if i == 0: names += [('var%d(t)' % (j+1)) for j in range(n_vars)] else: names += [('var%d(t+%d)' % (j+1, i)) for j in range(n_vars)] # put it all together agg = concat(cols, axis=1) agg.columns = names # drop rows with NaN values if dropnan: agg.dropna(inplace=True) return agg # load dataset dataset = read_csv('pollution.csv', header=0, index_col=0) values = dataset.values # integer encode direction encoder = LabelEncoder() values[:,4] = encoder.fit_transform(values[:,4]) # ensure all data is float values = values.astype('float32') # normalize features scaler = MinMaxScaler(feature_range=(0, 1)) scaled = scaler.fit_transform(values) # frame as supervised learning reframed = series_to_supervised(scaled, 1, 1) # drop columns we don't want to predict reframed.drop(reframed.columns[[9,10,11,12,13,14,15]], axis=1, inplace=True) print(reframed.head())
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 |
# prepare data for lstm from pandas import read_csv from pandas import DataFrame from pandas import concat from sklearn.preprocessing import LabelEncoder from sklearn.preprocessing import MinMaxScaler
# convert series to supervised learning def series_to_supervised(data, n_in=1, n_out=1, dropnan=True): n_vars = 1 if type(data) is list else data.shape[1] df = DataFrame(data) cols, names = list(), list() # input sequence (t-n, ... t-1) for i in range(n_in, 0, -1): cols.append(df.shift(i)) names += [('var%d(t-%d)' % (j+1, i)) for j in range(n_vars)] # forecast sequence (t, t+1, ... t+n) for i in range(0, n_out): cols.append(df.shift(-i)) if i == 0: names += [('var%d(t)' % (j+1)) for j in range(n_vars)] else: names += [('var%d(t+%d)' % (j+1, i)) for j in range(n_vars)] # put it all together agg = concat(cols, axis=1) agg.columns = names # drop rows with NaN values if dropnan: agg.dropna(inplace=True) return agg
# load dataset dataset = read_csv('pollution.csv', header=0, index_col=0) values = dataset.values # integer encode direction encoder = LabelEncoder() values[:,4] = encoder.fit_transform(values[:,4]) # ensure all data is float values = values.astype('float32') # normalize features scaler = MinMaxScaler(feature_range=(0, 1)) scaled = scaler.fit_transform(values) # frame as supervised learning reframed = series_to_supervised(scaled, 1, 1) # drop columns we don't want to predict reframed.drop(reframed.columns[[9,10,11,12,13,14,15]], axis=1, inplace=True) print(reframed.head()) |
Running the example prints the first 5 rows of the transformed dataset. We can see the 8 input variables (input series) and the 1 output variable (pollution level at the current hour).
var1(t-1) var2(t-1) var3(t-1) var4(t-1) var5(t-1) var6(t-1) \ 1 0.129779 0.352941 0.245902 0.527273 0.666667 0.002290 2 0.148893 0.367647 0.245902 0.527273 0.666667 0.003811 3 0.159960 0.426471 0.229508 0.545454 0.666667 0.005332 4 0.182093 0.485294 0.229508 0.563637 0.666667 0.008391 5 0.138833 0.485294 0.229508 0.563637 0.666667 0.009912 var7(t-1) var8(t-1) var1(t) 1 0.000000 0.0 0.148893 2 0.000000 0.0 0.159960 3 0.000000 0.0 0.182093 4 0.037037 0.0 0.138833 5 0.074074 0.0 0.109658
| 1 2 3 4 5 6 7 8 9 10 11 12 13 |
var1(t-1) var2(t-1) var3(t-1) var4(t-1) var5(t-1) var6(t-1) \ 1 0.129779 0.352941 0.245902 0.527273 0.666667 0.002290 2 0.148893 0.367647 0.245902 0.527273 0.666667 0.003811 3 0.159960 0.426471 0.229508 0.545454 0.666667 0.005332 4 0.182093 0.485294 0.229508 0.563637 0.666667 0.008391 5 0.138833 0.485294 0.229508 0.563637 0.666667 0.009912 var7(t-1) var8(t-1) var1(t) 1 0.000000 0.0 0.148893 2 0.000000 0.0 0.159960 3 0.000000 0.0 0.182093 4 0.037037 0.0 0.138833 5 0.074074 0.0 0.109658 |
This data preparation is simple and there is more we could explore. Some ideas you could look at include:
- One-hot encoding wind direction.
- Making all series stationary with differencing and seasonal adjustment.
- Providing more than 1 hour of input time steps.
This last point is perhaps the most important given the use of Backpropagation through time by LSTMs when learning sequence prediction problems.
Define and Fit Model
In this section, we will fit an LSTM on the multivariate input data.
First, we must split the prepared dataset into train and test sets. To speed up the training of the model for this demonstration, we will only fit the model on the first year of data, then evaluate it on the remaining 4 years of data. If you have time, consider exploring the inverted version of this test harness.
The example below splits the dataset into train and test sets, then splits the train and test sets into input and output variables. Finally, the inputs (X) are reshaped into the 3D format expected by LSTMs, namely [samples, timesteps, features].
... # split into train and test sets values = reframed.values n_train_hours = 365 * 24 train = values[:n_train_hours, :] test = values[n_train_hours:, :] # split into input and outputs train_X, train_y = train[:, :-1], train[:, -1] test_X, test_y = test[:, :-1], test[:, -1] # reshape input to be 3D [samples, timesteps, features] train_X = train_X.reshape((train_X.shape[0], 1, train_X.shape[1])) test_X = test_X.reshape((test_X.shape[0], 1, test_X.shape[1])) print(train_X.shape, train_y.shape, test_X.shape, test_y.shape)
| 1 2 3 4 5 6 7 8 9 10 11 12 13 |
... # split into train and test sets values = reframed.values n_train_hours = 365 * 24 train = values[:n_train_hours, :] test = values[n_train_hours:, :] # split into input and outputs train_X, train_y = train[:, :-1], train[:, -1] test_X, test_y = test[:, :-1], test[:, -1] # reshape input to be 3D [samples, timesteps, features] train_X = train_X.reshape((train_X.shape[0], 1, train_X.shape[1])) test_X = test_X.reshape((test_X.shape[0], 1, test_X.shape[1])) print(train_X.shape, train_y.shape, test_X.shape, test_y.shape) |
Running this example prints the shape of the train and test input and output sets with about 9K hours of data for training and about 35K hours for testing.
(8760, 1, 8) (8760,) (35039, 1, 8) (35039,)
| 1 |
(8760, 1, 8) (8760,) (35039, 1, 8) (35039,) |
Now we can define and fit our LSTM model.
We will define the LSTM with 50 neurons in the first hidden layer and 1 neuron in the output layer for predicting pollution. The input shape will be 1 time step with 8 features.
We will use the Mean Absolute Error (MAE) loss function and the efficient Adam version of stochastic gradient descent.
The model will be fit for 50 training epochs with a batch size of 72. Remember that the internal state of the LSTM in Keras is reset at the end of each batch, so an internal state that is a function of a number of days may be helpful (try testing this).
Finally, we keep track of both the training and test loss during training by setting the validation_data argument in the fit() function. At the end of the run both the training and test loss are plotted.
... # design network model = Sequential() model.add(LSTM(50, input_shape=(train_X.shape[1], train_X.shape[2]))) model.add(Dense(1)) model.compile(loss='mae', optimizer='adam') # fit network history = model.fit(train_X, train_y, epochs=50, batch_size=72, validation_data=(test_X, test_y), verbose=2, shuffle=False) # plot history pyplot.plot(history.history['loss'], label='train') pyplot.plot(history.history['val_loss'], label='test') pyplot.legend() pyplot.show()
| 1 2 3 4 5 6 7 8 9 10 11 12 13 |
... # design network model = Sequential() model.add(LSTM(50, input_shape=(train_X.shape[1], train_X.shape[2]))) model.add(Dense(1)) model.compile(loss='mae', optimizer='adam') # fit network history = model.fit(train_X, train_y, epochs=50, batch_size=72, validation_data=(test_X, test_y), verbose=2, shuffle=False) # plot history pyplot.plot(history.history['loss'], label='train') pyplot.plot(history.history['val_loss'], label='test') pyplot.legend() pyplot.show() |
Evaluate Model
After the model is fit, we can forecast for the entire test dataset.
We combine the forecast with the test dataset and invert the scaling. We also invert scaling on the test dataset with the expected pollution numbers.
With forecasts and actual values in their original scale, we can then calculate an error score for the model. In this case, we calculate the Root Mean Squared Error (RMSE) that gives error in the same units as the variable itself.
... # make a prediction yhat = model.predict(test_X) test_X = test_X.reshape((test_X.shape[0], test_X.shape[2])) # invert scaling for forecast inv_yhat = concatenate((yhat, test_X[:, 1:]), axis=1) inv_yhat = scaler.inverse_transform(inv_yhat) inv_yhat = inv_yhat[:,0] # invert scaling for actual test_y = test_y.reshape((len(test_y), 1)) inv_y = concatenate((test_y, test_X[:, 1:]), axis=1) inv_y = scaler.inverse_transform(inv_y) inv_y = inv_y[:,0] # calculate RMSE rmse = sqrt(mean_squared_error(inv_y, inv_yhat)) print('Test RMSE: %.3f' % rmse)
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
... # make a prediction yhat = model.predict(test_X) test_X = test_X.reshape((test_X.shape[0], test_X.shape[2])) # invert scaling for forecast inv_yhat = concatenate((yhat, test_X[:, 1:]), axis=1) inv_yhat = scaler.inverse_transform(inv_yhat) inv_yhat = inv_yhat[:,0] # invert scaling for actual test_y = test_y.reshape((len(test_y), 1)) inv_y = concatenate((test_y, test_X[:, 1:]), axis=1) inv_y = scaler.inverse_transform(inv_y) inv_y = inv_y[:,0] # calculate RMSE rmse = sqrt(mean_squared_error(inv_y, inv_yhat)) print('Test RMSE: %.3f' % rmse) |
Complete Example
The complete example is listed below.
NOTE: This example assumes you have prepared the data correctly, e.g. converted the downloaded “raw.csv” to the prepared “pollution.csv“. See the first part of this tutorial.
from math import sqrt from numpy import concatenate from matplotlib import pyplot from pandas import read_csv from pandas import DataFrame from pandas import concat from sklearn.preprocessing import MinMaxScaler from sklearn.preprocessing import LabelEncoder from sklearn.metrics import mean_squared_error from keras.models import Sequential from keras.layers import Dense from keras.layers import LSTM # convert series to supervised learning def series_to_supervised(data, n_in=1, n_out=1, dropnan=True): n_vars = 1 if type(data) is list else data.shape[1] df = DataFrame(data) cols, names = list(), list() # input sequence (t-n, ... t-1) for i in range(n_in, 0, -1): cols.append(df.shift(i)) names += [('var%d(t-%d)' % (j+1, i)) for j in range(n_vars)] # forecast sequence (t, t+1, ... t+n) for i in range(0, n_out): cols.append(df.shift(-i)) if i == 0: names += [('var%d(t)' % (j+1)) for j in range(n_vars)] else: names += [('var%d(t+%d)' % (j+1, i)) for j in range(n_vars)] # put it all together agg = concat(cols, axis=1) agg.columns = names # drop rows with NaN values if dropnan: agg.dropna(inplace=True) return agg # load dataset dataset = read_csv('pollution.csv', header=0, index_col=0) values = dataset.values # integer encode direction encoder = LabelEncoder() values[:,4] = encoder.fit_transform(values[:,4]) # ensure all data is float values = values.astype('float32') # normalize features scaler = MinMaxScaler(feature_range=(0, 1)) scaled = scaler.fit_transform(values) # frame as supervised learning reframed = series_to_supervised(scaled, 1, 1) # drop columns we don't want to predict reframed.drop(reframed.columns[[9,10,11,12,13,14,15]], axis=1, inplace=True) print(reframed.head()) # split into train and test sets values = reframed.values n_train_hours = 365 * 24 train = values[:n_train_hours, :] test = values[n_train_hours:, :] # split into input and outputs train_X, train_y = train[:, :-1], train[:, -1] test_X, test_y = test[:, :-1], test[:, -1] # reshape input to be 3D [samples, timesteps, features] train_X = train_X.reshape((train_X.shape[0], 1, train_X.shape[1])) test_X = test_X.reshape((test_X.shape[0], 1, test_X.shape[1])) print(train_X.shape, train_y.shape, test_X.shape, test_y.shape) # design network model = Sequential() model.add(LSTM(50, input_shape=(train_X.shape[1], train_X.shape[2]))) model.add(Dense(1)) model.compile(loss='mae', optimizer='adam') # fit network history = model.fit(train_X, train_y, epochs=50, batch_size=72, validation_data=(test_X, test_y), verbose=2, shuffle=False) # plot history pyplot.plot(history.history['loss'], label='train') pyplot.plot(history.history['val_loss'], label='test') pyplot.legend() pyplot.show() # make a prediction yhat = model.predict(test_X) test_X = test_X.reshape((test_X.shape[0], test_X.shape[2])) # invert scaling for forecast inv_yhat = concatenate((yhat, test_X[:, 1:]), axis=1) inv_yhat = scaler.inverse_transform(inv_yhat) inv_yhat = inv_yhat[:,0] # invert scaling for actual test_y = test_y.reshape((len(test_y), 1)) inv_y = concatenate((test_y, test_X[:, 1:]), axis=1) inv_y = scaler.inverse_transform(inv_y) inv_y = inv_y[:,0] # calculate RMSE rmse = sqrt(mean_squared_error(inv_y, inv_yhat)) print('Test RMSE: %.3f' % rmse)
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 |
from math import sqrt from numpy import concatenate from matplotlib import pyplot from pandas import read_csv from pandas import DataFrame from pandas import concat from sklearn.preprocessing import MinMaxScaler from sklearn.preprocessing import LabelEncoder from sklearn.metrics import mean_squared_error from keras.models import Sequential from keras.layers import Dense from keras.layers import LSTM # convert series to supervised learning def series_to_supervised(data, n_in=1, n_out=1, dropnan=True): n_vars = 1 if type(data) is list else data.shape[1] df = DataFrame(data) cols, names = list(), list() # input sequence (t-n, ... t-1) for i in range(n_in, 0, -1): cols.append(df.shift(i)) names += [('var%d(t-%d)' % (j+1, i)) for j in range(n_vars)] # forecast sequence (t, t+1, ... t+n) for i in range(0, n_out): cols.append(df.shift(-i)) if i == 0: names += [('var%d(t)' % (j+1)) for j in range(n_vars)] else: names += [('var%d(t+%d)' % (j+1, i)) for j in range(n_vars)] # put it all together agg = concat(cols, axis=1) agg.columns = names # drop rows with NaN values if dropnan: agg.dropna(inplace=True) return agg # load dataset dataset = read_csv('pollution.csv', header=0, index_col=0) values = dataset.values # integer encode direction encoder = LabelEncoder() values[:,4] = encoder.fit_transform(values[:,4]) # ensure all data is float values = values.astype('float32') # normalize features scaler = MinMaxScaler(feature_range=(0, 1)) scaled = scaler.fit_transform(values) # frame as supervised learning reframed = series_to_supervised(scaled, 1, 1) # drop columns we don't want to predict reframed.drop(reframed.columns[[9,10,11,12,13,14,15]], axis=1, inplace=True) print(reframed.head()) # split into train and test sets values = reframed.values n_train_hours = 365 * 24 train = values[:n_train_hours, :] test = values[n_train_hours:, :] # split into input and outputs train_X, train_y = train[:, :-1], train[:, -1] test_X, test_y = test[:, :-1], test[:, -1] # reshape input to be 3D [samples, timesteps, features] train_X = train_X.reshape((train_X.shape[0], 1, train_X.shape[1])) test_X = test_X.reshape((test_X.shape[0], 1, test_X.shape[1])) print(train_X.shape, train_y.shape, test_X.shape, test_y.shape) # design network model = Sequential() model.add(LSTM(50, input_shape=(train_X.shape[1], train_X.shape[2]))) model.add(Dense(1)) model.compile(loss='mae', optimizer='adam') # fit network history = model.fit(train_X, train_y, epochs=50, batch_size=72, validation_data=(test_X, test_y), verbose=2, shuffle=False) # plot history pyplot.plot(history.history['loss'], label='train') pyplot.plot(history.history['val_loss'], label='test') pyplot.legend() pyplot.show() # make a prediction yhat = model.predict(test_X) test_X = test_X.reshape((test_X.shape[0], test_X.shape[2])) # invert scaling for forecast inv_yhat = concatenate((yhat, test_X[:, 1:]), axis=1) inv_yhat = scaler.inverse_transform(inv_yhat) inv_yhat = inv_yhat[:,0] # invert scaling for actual test_y = test_y.reshape((len(test_y), 1)) inv_y = concatenate((test_y, test_X[:, 1:]), axis=1) inv_y = scaler.inverse_transform(inv_y) inv_y = inv_y[:,0] # calculate RMSE rmse = sqrt(mean_squared_error(inv_y, inv_yhat)) print('Test RMSE: %.3f' % rmse) |
Running the example first creates a plot showing the train and test loss during training.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
Interestingly, we can see that test loss drops below training loss. The model may be overfitting the training data. Measuring and plotting RMSE during training may shed more light on this.
Line Plot of Train and Test Loss from the Multivariate LSTM During Training
The Train and test loss are printed at the end of each training epoch. At the end of the run, the final RMSE of the model on the test dataset is printed.
We can see that the model achieves a respectable RMSE of 26.496, which is lower than an RMSE of 30 found with a persistence model.
... Epoch 46/50 0s - loss: 0.0143 - val_loss: 0.0133 Epoch 47/50 0s - loss: 0.0143 - val_loss: 0.0133 Epoch 48/50 0s - loss: 0.0144 - val_loss: 0.0133 Epoch 49/50 0s - loss: 0.0143 - val_loss: 0.0133 Epoch 50/50 0s - loss: 0.0144 - val_loss: 0.0133 Test RMSE: 26.496
| 1 2 3 4 5 6 7 8 9 10 11 12 |
... Epoch 46/50 0s - loss: 0.0143 - val_loss: 0.0133 Epoch 47/50 0s - loss: 0.0143 - val_loss: 0.0133 Epoch 48/50 0s - loss: 0.0144 - val_loss: 0.0133 Epoch 49/50 0s - loss: 0.0143 - val_loss: 0.0133 Epoch 50/50 0s - loss: 0.0144 - val_loss: 0.0133 Test RMSE: 26.496 |
This model is not tuned. Can you do better?
Let me know your problem framing, model configuration, and RMSE in the comments below.
Train On Multiple Lag Timesteps Example
There have been many requests for advice on how to adapt the above example to train the model on multiple previous time steps.
I had tried this and a myriad of other configurations when writing the original post and decided not to include them because they did not lift model skill.
Nevertheless, I have included this example below as reference template that you could adapt for your own problems.
The changes needed to train the model on multiple previous time steps are quite minimal, as follows:
First, you must frame the problem suitably when calling series_to_supervised(). We will use 3 hours of data as input. Also note, we no longer explictly drop the columns from all of the other fields at ob(t).
... # specify the number of lag hours n_hours = 3 n_features = 8 # frame as supervised learning reframed = series_to_supervised(scaled, n_hours, 1)
| 1 2 3 4 5 6 |
... # specify the number of lag hours n_hours = 3 n_features = 8 # frame as supervised learning reframed = series_to_supervised(scaled, n_hours, 1) |
Next, we need to be more careful in specifying the column for input and output.
We have 3 * 8 + 8 columns in our framed dataset. We will take 3 * 8 or 24 columns as input for the obs of all features across the previous 3 hours. We will take just the pollution variable as output at the following hour, as follows:
... # split into input and outputs n_obs = n_hours * n_features train_X, train_y = train[:, :n_obs], train[:, -n_features] test_X, test_y = test[:, :n_obs], test[:, -n_features] print(train_X.shape, len(train_X), train_y.shape)
| 1 2 3 4 5 6 |
... # split into input and outputs n_obs = n_hours * n_features train_X, train_y = train[:, :n_obs], train[:, -n_features] test_X, test_y = test[:, :n_obs], test[:, -n_features] print(train_X.shape, len(train_X), train_y.shape) |
Next, we can reshape our input data correctly to reflect the time steps and features.
... # reshape input to be 3D [samples, timesteps, features] train_X = train_X.reshape((train_X.shape[0], n_hours, n_features)) test_X = test_X.reshape((test_X.shape[0], n_hours, n_features))
| 1 2 3 4 |
... # reshape input to be 3D [samples, timesteps, features] train_X = train_X.reshape((train_X.shape[0], n_hours, n_features)) test_X = test_X.reshape((test_X.shape[0], n_hours, n_features)) |
Fitting the model is the same.
The only other small change is in how to evaluate the model. Specifically, in how we reconstruct the rows with 8 columns suitable for reversing the scaling operation to get the y and yhat back into the original scale so that we can calculate the RMSE.
The gist of the change is that we concatenate the y or yhat column with the last 7 features of the test dataset in order to inverse the scaling, as follows:
... # invert scaling for forecast inv_yhat = concatenate((yhat, test_X[:, -7:]), axis=1) inv_yhat = scaler.inverse_transform(inv_yhat) inv_yhat = inv_yhat[:,0] # invert scaling for actual test_y = test_y.reshape((len(test_y), 1)) inv_y = concatenate((test_y, test_X[:, -7:]), axis=1) inv_y = scaler.inverse_transform(inv_y) inv_y = inv_y[:,0]
| 1 2 3 4 5 6 7 8 9 10 |
... # invert scaling for forecast inv_yhat = concatenate((yhat, test_X[:, -7:]), axis=1) inv_yhat = scaler.inverse_transform(inv_yhat) inv_yhat = inv_yhat[:,0] # invert scaling for actual test_y = test_y.reshape((len(test_y), 1)) inv_y = concatenate((test_y, test_X[:, -7:]), axis=1) inv_y = scaler.inverse_transform(inv_y) inv_y = inv_y[:,0] |
We can tie all of these modifications to the above example together. The complete example of multvariate time series forecasting with multiple lag inputs is listed below:
from math import sqrt from numpy import concatenate from matplotlib import pyplot from pandas import read_csv from pandas import DataFrame from pandas import concat from sklearn.preprocessing import MinMaxScaler from sklearn.preprocessing import LabelEncoder from sklearn.metrics import mean_squared_error from keras.models import Sequential from keras.layers import Dense from keras.layers import LSTM # convert series to supervised learning def series_to_supervised(data, n_in=1, n_out=1, dropnan=True): n_vars = 1 if type(data) is list else data.shape[1] df = DataFrame(data) cols, names = list(), list() # input sequence (t-n, ... t-1) for i in range(n_in, 0, -1): cols.append(df.shift(i)) names += [('var%d(t-%d)' % (j+1, i)) for j in range(n_vars)] # forecast sequence (t, t+1, ... t+n) for i in range(0, n_out): cols.append(df.shift(-i)) if i == 0: names += [('var%d(t)' % (j+1)) for j in range(n_vars)] else: names += [('var%d(t+%d)' % (j+1, i)) for j in range(n_vars)] # put it all together agg = concat(cols, axis=1) agg.columns = names # drop rows with NaN values if dropnan: agg.dropna(inplace=True) return agg # load dataset dataset = read_csv('pollution.csv', header=0, index_col=0) values = dataset.values # integer encode direction encoder = LabelEncoder() values[:,4] = encoder.fit_transform(values[:,4]) # ensure all data is float values = values.astype('float32') # normalize features scaler = MinMaxScaler(feature_range=(0, 1)) scaled = scaler.fit_transform(values) # specify the number of lag hours n_hours = 3 n_features = 8 # frame as supervised learning reframed = series_to_supervised(scaled, n_hours, 1) print(reframed.shape) # split into train and test sets values = reframed.values n_train_hours = 365 * 24 train = values[:n_train_hours, :] test = values[n_train_hours:, :] # split into input and outputs n_obs = n_hours * n_features train_X, train_y = train[:, :n_obs], train[:, -n_features] test_X, test_y = test[:, :n_obs], test[:, -n_features] print(train_X.shape, len(train_X), train_y.shape) # reshape input to be 3D [samples, timesteps, features] train_X = train_X.reshape((train_X.shape[0], n_hours, n_features)) test_X = test_X.reshape((test_X.shape[0], n_hours, n_features)) print(train_X.shape, train_y.shape, test_X.shape, test_y.shape) # design network model = Sequential() model.add(LSTM(50, input_shape=(train_X.shape[1], train_X.shape[2]))) model.add(Dense(1)) model.compile(loss='mae', optimizer='adam') # fit network history = model.fit(train_X, train_y, epochs=50, batch_size=72, validation_data=(test_X, test_y), verbose=2, shuffle=False) # plot history pyplot.plot(history.history['loss'], label='train') pyplot.plot(history.history['val_loss'], label='test') pyplot.legend() pyplot.show() # make a prediction yhat = model.predict(test_X) test_X = test_X.reshape((test_X.shape[0], n_hours*n_features)) # invert scaling for forecast inv_yhat = concatenate((yhat, test_X[:, -7:]), axis=1) inv_yhat = scaler.inverse_transform(inv_yhat) inv_yhat = inv_yhat[:,0] # invert scaling for actual test_y = test_y.reshape((len(test_y), 1)) inv_y = concatenate((test_y, test_X[:, -7:]), axis=1) inv_y = scaler.inverse_transform(inv_y) inv_y = inv_y[:,0] # calculate RMSE rmse = sqrt(mean_squared_error(inv_y, inv_yhat)) print('Test RMSE: %.3f' % rmse)
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 |
from math import sqrt from numpy import concatenate from matplotlib import pyplot from pandas import read_csv from pandas import DataFrame from pandas import concat from sklearn.preprocessing import MinMaxScaler from sklearn.preprocessing import LabelEncoder from sklearn.metrics import mean_squared_error from keras.models import Sequential from keras.layers import Dense from keras.layers import LSTM
# convert series to supervised learning def series_to_supervised(data, n_in=1, n_out=1, dropnan=True): n_vars = 1 if type(data) is list else data.shape[1] df = DataFrame(data) cols, names = list(), list() # input sequence (t-n, ... t-1) for i in range(n_in, 0, -1): cols.append(df.shift(i)) names += [('var%d(t-%d)' % (j+1, i)) for j in range(n_vars)] # forecast sequence (t, t+1, ... t+n) for i in range(0, n_out): cols.append(df.shift(-i)) if i == 0: names += [('var%d(t)' % (j+1)) for j in range(n_vars)] else: names += [('var%d(t+%d)' % (j+1, i)) for j in range(n_vars)] # put it all together agg = concat(cols, axis=1) agg.columns = names # drop rows with NaN values if dropnan: agg.dropna(inplace=True) return agg
# load dataset dataset = read_csv('pollution.csv', header=0, index_col=0) values = dataset.values # integer encode direction encoder = LabelEncoder() values[:,4] = encoder.fit_transform(values[:,4]) # ensure all data is float values = values.astype('float32') # normalize features scaler = MinMaxScaler(feature_range=(0, 1)) scaled = scaler.fit_transform(values) # specify the number of lag hours n_hours = 3 n_features = 8 # frame as supervised learning reframed = series_to_supervised(scaled, n_hours, 1) print(reframed.shape)
# split into train and test sets values = reframed.values n_train_hours = 365 * 24 train = values[:n_train_hours, :] test = values[n_train_hours:, :] # split into input and outputs n_obs = n_hours * n_features train_X, train_y = train[:, :n_obs], train[:, -n_features] test_X, test_y = test[:, :n_obs], test[:, -n_features] print(train_X.shape, len(train_X), train_y.shape) # reshape input to be 3D [samples, timesteps, features] train_X = train_X.reshape((train_X.shape[0], n_hours, n_features)) test_X = test_X.reshape((test_X.shape[0], n_hours, n_features)) print(train_X.shape, train_y.shape, test_X.shape, test_y.shape)
# design network model = Sequential() model.add(LSTM(50, input_shape=(train_X.shape[1], train_X.shape[2]))) model.add(Dense(1)) model.compile(loss='mae', optimizer='adam') # fit network history = model.fit(train_X, train_y, epochs=50, batch_size=72, validation_data=(test_X, test_y), verbose=2, shuffle=False) # plot history pyplot.plot(history.history['loss'], label='train') pyplot.plot(history.history['val_loss'], label='test') pyplot.legend() pyplot.show()
# make a prediction yhat = model.predict(test_X) test_X = test_X.reshape((test_X.shape[0], n_hours*n_features)) # invert scaling for forecast inv_yhat = concatenate((yhat, test_X[:, -7:]), axis=1) inv_yhat = scaler.inverse_transform(inv_yhat) inv_yhat = inv_yhat[:,0] # invert scaling for actual test_y = test_y.reshape((len(test_y), 1)) inv_y = concatenate((test_y, test_X[:, -7:]), axis=1) inv_y = scaler.inverse_transform(inv_y) inv_y = inv_y[:,0] # calculate RMSE rmse = sqrt(mean_squared_error(inv_y, inv_yhat)) print('Test RMSE: %.3f' % rmse) |
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
The model is fit as before in a minute or two.
... Epoch 45/50 1s - loss: 0.0143 - val_loss: 0.0154 Epoch 46/50 1s - loss: 0.0143 - val_loss: 0.0148 Epoch 47/50 1s - loss: 0.0143 - val_loss: 0.0152 Epoch 48/50 1s - loss: 0.0143 - val_loss: 0.0151 Epoch 49/50 1s - loss: 0.0143 - val_loss: 0.0152 Epoch 50/50 1s - loss: 0.0144 - val_loss: 0.0149
| 1 2 3 4 5 6 7 8 9 10 11 12 13 |
... Epoch 45/50 1s - loss: 0.0143 - val_loss: 0.0154 Epoch 46/50 1s - loss: 0.0143 - val_loss: 0.0148 Epoch 47/50 1s - loss: 0.0143 - val_loss: 0.0152 Epoch 48/50 1s - loss: 0.0143 - val_loss: 0.0151 Epoch 49/50 1s - loss: 0.0143 - val_loss: 0.0152 Epoch 50/50 1s - loss: 0.0144 - val_loss: 0.0149 |
A plot of train and test loss over the epochs is plotted.
Plot of Loss on the Train and Test Datasets
Finally, the Test RMSE is printed, not really showing any advantage in skill, at least on this problem.
Test RMSE: 27.177
| 1 |
Test RMSE: 27.177 |
I would add that the LSTM does not appear to be suitable for autoregression type problems and that you may be better off exploring an MLP with a large window.
I hope this example helps you with your own time series forecasting experiments.
Further Reading
This section provides more resources on the topic if you are looking go deeper.
- Beijing PM2.5 Data Set on the UCI Machine Learning Repository
- The 5 Step Life-Cycle for Long Short-Term Memory Models in Keras
- Time Series Forecasting with the Long Short-Term Memory Network in Python
- Multi-step Time Series Forecasting with Long Short-Term Memory Networks in Python
Summary
In this tutorial, you discovered how to fit an LSTM to a multivariate time series forecasting problem.
Specifically, you learned:
- How to transform a raw dataset into something we can use for time series forecasting.
- How to prepare data and fit an LSTM for a multivariate time series forecasting problem.
- How to make a forecast and rescale the result back into the original units.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.
讨论见:https://machinelearningmastery.com/multivariate-time-series-forecasting-lstms-keras/
中文翻译,参见:https://blog.csdn.net/qq_28031525/article/details/79046718
本文翻译自Jason Brownlee的博客Multivariate Time Series Forecasting with LSTMs in Keras
传统的线性模型难以解决多变量或多输入问题,而神经网络如LSTM则擅长于处理多个变量的问题,该特性使其有助于解决时间序列预测问题。
在接下来的这篇博客中,你将学会如何利用深度学习库Keras搭建LSTM模型来处理多个变量的时间序列预测问题。
经过这个博客你会掌握:
1. 如何将原始数据转化为适合处理时序预测问题的数据格式;
2. 如何准备数据并搭建LSTM来处理时序预测问题;
3. 如何利用模型预测。
目录
-
-
- 1.空气污染预测
- 2.数据处理
- 3.多变量LSTM预测模型
-
- 3.1 LSTM数据准备
- 3.2 构造模型
- 3.3 模型评估
-
- 4.进一步阅读
-
1.空气污染预测
在这篇博客中,我们将采用空气质量数据集。数据来源自位于北京的美国大使馆在2010年至2014年共5年间每小时采集的天气及空气污染指数。
数据集包括日期、PM2.5浓度、露点、温度、风向、风速、累积小时雪量和累积小时雨量。原始数据中完整的特征如下:
1.No 行数
2.year 年
3.month 月
4.day 日
5.hour 小时
6.pm2.5 PM2.5浓度
7.DEWP 露点
8.TEMP 温度
9.PRES 大气压
10.cbwd 风向
11.lws 风速
12.ls 累积雪量
13.lr 累积雨量 我们可以利用此数据集搭建预测模型,利用前一个或几个小时的天气条件和污染数据预测下一个(当前)时刻的污染程度。
可以在UCI Machine Learning Repository下载数据集。
Beijing PM2.5 Data Set
2.数据处理
在使用数据之前需要对数据做一些处理,待处理部分数据如下:
No,year,month,day,hour,pm2.5,DEWP,TEMP,PRES,cbwd,Iws,Is,Ir
1,2010,1,1,0,NA,-21,-11,1021,NW,1.79,0,0
2,2010,1,1,1,NA,-21,-12,1020,NW,4.92,0,0
3,2010,1,1,2,NA,-21,-11,1019,NW,6.71,0,0
4,2010,1,1,3,NA,-21,-14,1019,NW,9.84,0,0
5,2010,1,1,4,NA,-20,-12,1018,NW,12.97,0,0 粗略的观察数据集会发现最开始的24小时PM2.5值都是NA,因此需要删除这部分数据,对于其他时刻少量的缺省值利用Pandas中的fillna填充;同时需要整合日期数据,使其作为Pandas中索引(index)。
下面的代码完成了以上的处理过程,同时去掉了原始数据中“No”列,并将列命名为更清晰的名字。
from pandas import read_csv
from datetime import datetime
# load data
def parse(x):
return datetime.strptime(x, '%Y %m %d %H')
dataset = read_csv('raw.csv', parse_dates = [['year', 'month', 'day', 'hour']], index_col=0, date_parser=parse)
dataset.drop('No', axis=1, inplace=True)
# manually specify column names
dataset.columns = ['pollution', 'dew', 'temp', 'press', 'wnd_dir', 'wnd_spd', 'snow', 'rain']
dataset.index.name = 'date'
# mark all NA values with 0
dataset['pollution'].fillna(0, inplace=True)
# drop the first 24 hours
dataset = dataset[24:]
# summarize first 5 rows
print(dataset.head(5))
# save to file
dataset.to_csv('pollution.csv')处理后的数据存储在“pollution.csv”文件中,部分如下:
pollution dew temp press wnd_dir wnd_spd snow rain
date
2010-01-02 00:00:00 129.0 -16 -4.0 1020.0 SE 1.79 0 0
2010-01-02 01:00:00 148.0 -15 -4.0 1020.0 SE 2.68 0 0
2010-01-02 02:00:00 159.0 -11 -5.0 1021.0 SE 3.57 0 0
2010-01-02 03:00:00 181.0 -7 -5.0 1022.0 SE 5.36 1 0
2010-01-02 04:00:00 138.0 -7 -5.0 1022.0 SE 6.25 2 0现在的数据格式已经更加适合处理,可以简单的对每列进行绘图。下面的代码加载了“pollution.csv”文件,并对除了类别型特性“风速”的每一列数据分别绘图。
from pandas import read_csv
from matplotlib import pyplot
# load dataset
dataset = read_csv('pollution.csv', header=0, index_col=0)
values = dataset.values
# specify columns to plot
groups = [0, 1, 2, 3, 5, 6, 7]
i = 1
# plot each column
pyplot.figure()
for group in groups:
pyplot.subplot(len(groups), 1, i)
pyplot.plot(values[:, group])
pyplot.title(dataset.columns[group], y=0.5, loc='right')
i += 1
pyplot.show() 运行上述代码,并对7个变量在5年的范围内绘图。
![]()
3.多变量LSTM预测模型
3.1 LSTM数据准备
采用LSTM模型时,第一步需要对数据进行适配处理,其中包括将数据集转化为有监督学习问题和归一化变量(包括输入和输出值),使其能够实现通过前一个时刻(t-1)的污染数据和天气条件预测当前时刻(t)的污染。
以上的处理方式很直接也比较简单,仅仅只是为了抛砖引玉,其他的处理方式也可以探索,比如:
1. 利用过去24小时的污染数据和天气条件预测当前时刻的污染;
2. 预测下一个时刻(t+1)可能的天气条件;
利用上一篇博客中的series_to_supervised()函数将数据集转化为有监督学习问题:How to Convert a Time Series to a Supervised Learning Problem in Python
下面代码中首先加载“pollution.csv”文件,并利用sklearn的预处理模块对类别特征“风向”进行编码,当然也可以对该特征进行one-hot编码。
接着对所有的特征进行归一化处理,然后将数据集转化为有监督学习问题,同时将需要预测的当前时刻(t)的天气条件特征移除,完整代码如下:
# convert series to supervised learning
def series_to_supervised(data, n_in=1, n_out=1, dropnan=True):
n_vars = 1 if type(data) is list else data.shape[1]
df = DataFrame(data)
cols, names = list(), list()
# input sequence (t-n, ... t-1)
for i in range(n_in, 0, -1):
cols.append(df.shift(i))
names += [('var%d(t-%d)' % (j+1, i)) for j in range(n_vars)]
# forecast sequence (t, t+1, ... t+n)
for i in range(0, n_out):
cols.append(df.shift(-i))
if i == 0:
names += [('var%d(t)' % (j+1)) for j in range(n_vars)]
else:
names += [('var%d(t+%d)' % (j+1, i)) for j in range(n_vars)]
# put it all together
agg = concat(cols, axis=1)
agg.columns = names
# drop rows with NaN values
if dropnan:
agg.dropna(inplace=True)
return agg
# load dataset
dataset = read_csv('pollution.csv', header=0, index_col=0)
values = dataset.values
# integer encode direction
encoder = LabelEncoder()
values[:,4] = encoder.fit_transform(values[:,4])
# ensure all data is float
values = values.astype('float32')
# normalize features
scaler = MinMaxScaler(feature_range=(0, 1))
scaled = scaler.fit_transform(values)
# frame as supervised learning
reframed = series_to_supervised(scaled, 1, 1)
# drop columns we don't want to predict
reframed.drop(reframed.columns[[9,10,11,12,13,14,15]], axis=1, inplace=True)
print(reframed.head())
运行上述代码,能看到被转化后的数据集,数据集包括8个输入变量(输入特征)和1个输出变量(当前时刻t的空气污染值,标签)
为了使变量名更直观,笔者修改了series_to_supervised()源码。
pollution(t-1) dew(t-1) temp(t-1) press(t-1) wnd_dir(t-1) wnd_spd(t-1) \
1 0.129779 0.352941 0.245902 0.527273 0.666667 0.002290
2 0.148893 0.367647 0.245902 0.527273 0.666667 0.003811
3 0.159960 0.426471 0.229508 0.545454 0.666667 0.005332
4 0.182093 0.485294 0.229508 0.563637 0.666667 0.008391
5 0.138833 0.485294 0.229508 0.563637 0.666667 0.009912
snow(t-1) rain(t-1) pollution(t)
1 0.000000 0.0 0.148893
2 0.000000 0.0 0.159960
3 0.000000 0.0 0.182093
4 0.037037 0.0 0.138833
5 0.074074 0.0 0.109658 数据集的处理比较简单,还有很多的方式可以尝试,一些可以尝试的方向包括:
1. 对“风向”特征哑编码;
2. 加入季节特征;
3. 时间步长超过1。
其中,上述第三种方式对于处理时间序列问题的LSTM可能是最重要的。
3.2 构造模型
在这一节,我们将构造LSTM模型。
首先,我们需要将处理后的数据集划分为训练集和测试集。为了加速模型的训练,我们仅利用第一年数据进行训练,然后利用剩下的4年进行评估。
下面的代码将数据集进行划分,然后将训练集和测试集划分为输入和输出变量,最终将输入(X)改造为LSTM的输入格式,即[samples,timesteps,features]。
# split into train and test sets
values = reframed.values
n_train_hours = 365 * 24
train = values[:n_train_hours, :]
test = values[n_train_hours:, :]
# split into input and outputs
train_X, train_y = train[:, :-1], train[:, -1]
test_X, test_y = test[:, :-1], test[:, -1]
# reshape input to be 3D [samples, timesteps, features]
train_X = train_X.reshape((train_X.shape[0], 1, train_X.shape[1]))
test_X = test_X.reshape((test_X.shape[0], 1, test_X.shape[1]))
print(train_X.shape, train_y.shape, test_X.shape, test_y.shape)运行上述代码打印训练集和测试集的输入输出格式,其中9K小时数据作训练集,35K小时数据作测试集。
(8760, 1, 8) (8760,) (35039, 1, 8) (35039,) 现在可以搭建LSTM模型了。
LSTM模型中,隐藏层有50个神经元,输出层1个神经元(回归问题),输入变量是一个时间步(t-1)的特征,损失函数采用Mean Absolute Error(MAE),优化算法采用Adam,模型采用50个epochs并且每个batch的大小为72。
最后,在fit()函数中设置validation_data参数,记录训练集和测试集的损失,并在完成训练和测试后绘制损失图。
# design network
model = Sequential()
model.add(LSTM(50, input_shape=(train_X.shape[1], train_X.shape[2])))
model.add(Dense(1))
model.compile(loss='mae', optimizer='adam')
# fit network
history = model.fit(train_X, train_y, epochs=50, batch_size=72, validation_data=(test_X, test_y), verbose=2, shuffle=False)
# plot history
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
pyplot.show()
# design network
model = Sequential()
model.add(LSTM(50, input_shape=(train_X.shape[1], train_X.shape[2])))
model.add(Dense(1))
model.compile(loss='mae', optimizer='adam')
# fit network
history = model.fit(train_X, train_y, epochs=50, batch_size=72, validation_data=(test_X, test_y), verbose=2, shuffle=False)
# plot history
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
pyplot.show()3.3 模型评估
接下里我们对模型效果进行评估。
值得注意的是:需要将预测结果和部分测试集数据组合然后进行比例反转(invert the scaling),同时也需要将测试集上的预期值也进行比例转换。
(We combine the forecast with the test dataset and invert the scaling. We also invert scaling on the test dataset with the expected pollution numbers.)
至于在这里为什么进行比例反转,是因为我们将原始数据进行了预处理(连同输出值y),此时的误差损失计算是在处理之后的数据上进行的,为了计算在原始比例上的误差需要将数据进行转化。同时笔者有个小Tips:就是反转时的矩阵大小一定要和原来的大小(shape)完全相同,否则就会报错。
通过以上处理之后,再结合RMSE(均方根误差)计算损失。
# make a prediction
yhat = model.predict(test_X)
test_X = test_X.reshape((test_X.shape[0], test_X.shape[2]))
# invert scaling for forecast
inv_yhat = concatenate((yhat, test_X[:, 1:]), axis=1)
inv_yhat = scaler.inverse_transform(inv_yhat)
inv_yhat = inv_yhat[:,0]
# invert scaling for actual
test_y = test_y.reshape((len(test_y), 1))
inv_y = concatenate((test_y, test_X[:, 1:]), axis=1)
inv_y = scaler.inverse_transform(inv_y)
inv_y = inv_y[:,0]
# calculate RMSE
rmse = sqrt(mean_squared_error(inv_y, inv_yhat))
print('Test RMSE: %.3f' % rmse)
整个小项目完整代码如下,注意:下例代码假设你已经正确地完成了数据预处理过程,如将下载的“raw.csv” 数据处理成 “pollution.csv“文件中的数据。
from math import sqrt
from numpy import concatenate
from matplotlib import pyplot
from pandas import read_csv
from pandas import DataFrame
from pandas import concat
from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import LabelEncoder
from sklearn.metrics import mean_squared_error
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
# convert series to supervised learning
def series_to_supervised(data, n_in=1, n_out=1, dropnan=True):
n_vars = 1 if type(data) is list else data.shape[1]
df = DataFrame(data)
cols, names = list(), list()
# input sequence (t-n, ... t-1)
for i in range(n_in, 0, -1):
cols.append(df.shift(i))
names += [('var%d(t-%d)' % (j+1, i)) for j in range(n_vars)]
# forecast sequence (t, t+1, ... t+n)
for i in range(0, n_out):
cols.append(df.shift(-i))
if i == 0:
names += [('var%d(t)' % (j+1)) for j in range(n_vars)]
else:
names += [('var%d(t+%d)' % (j+1, i)) for j in range(n_vars)]
# put it all together
agg = concat(cols, axis=1)
agg.columns = names
# drop rows with NaN values
if dropnan:
agg.dropna(inplace=True)
return agg
# load dataset
dataset = read_csv('pollution.csv', header=0, index_col=0)
values = dataset.values
# integer encode direction
encoder = LabelEncoder()
values[:,4] = encoder.fit_transform(values[:,4])
# ensure all data is float
values = values.astype('float32')
# normalize features
scaler = MinMaxScaler(feature_range=(0, 1))
scaled = scaler.fit_transform(values)
# frame as supervised learning
reframed = series_to_supervised(scaled, 1, 1)
# drop columns we don't want to predict
reframed.drop(reframed.columns[[9,10,11,12,13,14,15]], axis=1, inplace=True)
print(reframed.head())
# split into train and test sets
values = reframed.values
n_train_hours = 365 * 24
train = values[:n_train_hours, :]
test = values[n_train_hours:, :]
# split into input and outputs
train_X, train_y = train[:, :-1], train[:, -1]
test_X, test_y = test[:, :-1], test[:, -1]
# reshape input to be 3D [samples, timesteps, features]
train_X = train_X.reshape((train_X.shape[0], 1, train_X.shape[1]))
test_X = test_X.reshape((test_X.shape[0], 1, test_X.shape[1]))
print(train_X.shape, train_y.shape, test_X.shape, test_y.shape)
# design network
model = Sequential()
model.add(LSTM(50, input_shape=(train_X.shape[1], train_X.shape[2])))
model.add(Dense(1))
model.compile(loss='mae', optimizer='adam')
# fit network
history = model.fit(train_X, train_y, epochs=50, batch_size=72, validation_data=(test_X, test_y), verbose=2, shuffle=False)
# plot history
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
pyplot.show()
# make a prediction
yhat = model.predict(test_X)
test_X = test_X.reshape((test_X.shape[0], test_X.shape[2]))
# invert scaling for forecast
inv_yhat = concatenate((yhat, test_X[:, 1:]), axis=1)
inv_yhat = scaler.inverse_transform(inv_yhat)
inv_yhat = inv_yhat[:,0]
# invert scaling for actual
test_y = test_y.reshape((len(test_y), 1))
inv_y = concatenate((test_y, test_X[:, 1:]), axis=1)
inv_y = scaler.inverse_transform(inv_y)
inv_y = inv_y[:,0]
# calculate RMSE
rmse = sqrt(mean_squared_error(inv_y, inv_yhat))
print('Test RMSE: %.3f' % rmse) 运行以上代码,首先将会绘制训练过程中的训练和测试损失图。
![]()
训练中的每个epoch都会记录和绘制训练集和测试集的损失,并在整个训练结束后绘制模型最终的RMSE。
下图中可以看到,整个模型的RMSE达到26.496。
...
Epoch 46/50
0s - loss: 0.0143 - val_loss: 0.0133
Epoch 47/50
0s - loss: 0.0143 - val_loss: 0.0133
Epoch 48/50
0s - loss: 0.0144 - val_loss: 0.0133
Epoch 49/50
0s - loss: 0.0143 - val_loss: 0.0133
Epoch 50/50
0s - loss: 0.0144 - val_loss: 0.0133
Test RMSE: 26.4964.进一步阅读
如果你想继续深入研究,本节提供更多的阅读资源:
1. Beijing PM2.5 Data Set on the UCI Machine Learning Repository
2. The 5 Step Life-Cycle for Long Short-Term Memory Models in Keras
3. Time Series Forecasting with the Long Short-Term Memory Network in Python
4. Multi-step Time Series Forecasting with Long Short-Term Memory Networks in Python
由于博客中代码展示不太方便,本人已将代码上传至Github中,欢迎指正交流。