优化算法之梯度下降算法整理
目录
-
- 1 介绍
- 2 优化方法
-
- 2.1 GD
- 2.2 SGD
- 2.3 mini-batch GD
- 2.4 Momentum
- 2.5 AdaGrad
- 2.6 RMSProp
- 2.7 Adam
- 3 总结
1 介绍
梯度下降 (Gradient Descent) 是一种经典的求极小值的算法，它的主要目的是通过迭代，使得模型参数沿负梯度不断的更新，目标函数逐渐收敛至局部极小值。
梯度下降是机器学习领域用途最广的优化算法，其分类也有多种，了解每种算法的原理是深度学习调参师的必备技能，也是面试中的高频问题，下面将根据算法的发展一一进行介绍。
2 优化方法
2.1 GD
GD是最为传统的梯度下降算法，是在全量的训练集上计算得到一个loss, 计算loss在每个参数上的梯度，然后对模型的参数执行一次更新，公式如下：（ η t \eta_{t} ηt为学习率， g t g_{t} gt为梯度向量）
GD的缺陷：遍历一遍训练集，才对权重进行一次更新，对于样本规模庞大的任务来说，GD的效率非常低下，算法收敛缓慢。
2.2 SGD
SGD (Stochastic Gradient Descent) 随机梯度下降主要是解决GD处理大规模任务效率低下的问题，它每次只随机抽取一个样本来计算loss，然后对参数执行一次更新，迭代速度快。
SGD的缺陷：loss的下降曲线抖动严重，因为根据单个样本的loss计算出的梯度不一定是正确更新方向，比如异常样本。SGD虽然加快了每次迭代的速度，但是达到算法收敛需要更多次的迭代，该方法适合数据不断到来的在线场景。
2.3 mini-batch GD
小批量梯度下降是GD与SGD折中的一种方法，使用全量的数据集计算loss效率低下，使用单个样本loss曲线方向不稳定，所以mini-batch GD使用批量数据来计算loss，样本数量是一个超参数，需要自行调整 (一般从2的幂次上进行选择,方便矩阵运算)。
mini-batch GD的缺陷：很显然，它继承了GD与SGD的优点，loss曲线下降方向比SGD更平稳，迭代效率比GD更高。但从另一个角度看，它也继承了两者的缺点不是么。
2.4 Momentum
Momentum 不同于前面的三种方法，它使用了一种动量的思想，使得loss曲线下降时方向抖动不那么严重。更新公式如下：
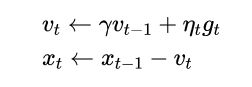在GD中，参数更新量 v t v_{t} vt 的值是 η t g t \eta_{t}g_{t} ηtgt， 只是根据当前的位置，沿梯度下降最大的方向更新，不考虑之前迭代下降的方向，这可能会使梯度方向抖动严重。
而 Momentum 动量法则会同时考虑之前的梯度方向 v t − 1 v_{t-1} vt−1 与该位置的梯度方向 g t g_{t} gt，保留了部分之前的梯度，使得下一次的梯度方向不会跟前一次相差太远，从而使得方向抖动不那么严重。如上式， γ \gamma γ 为动量超参数，用于控制前一轮梯度方向信息所占的比例，当 γ = 0 \gamma=0 γ=0 时退化成GD。
Momentum的缺陷：计算梯度时，所有参数的更新都是使用同一个学习率，即 g t g_{t} gt 向量中所有的梯度都共享学习率 η t \eta_{t} ηt。 如果有的参数梯度较大，则需要使用小学习率保证不会梯度爆炸，但又会导致梯度较小的参数更新太慢，所以需要每个参数拥有自己的学习率。
2.5 AdaGrad
AdaGrad 解决了所有参数共享同一学习率的问题。如下式所示：
对于每次迭代，用 S t S_{t} St 向量记录之前所有梯度 g t g_{t} gt 平方值的累加 (二阶动量)，初始时刻St为0。然后在计算更新量时，根据参数之前累积的各自的梯度平方值计算对应的学习率 (ϵ是为了避免除数为0而添加的常数)，梯度累加值大的参数对于小的学习率，反之对于大的学习率。
AdaGrad的缺陷：如果某个参数的梯度⼀直都较大，那么该参数的学习率将下降较快，更新也会越来越慢；反之，如果某权重的梯度⼀直都较小，那么该元素的学习率将下降较慢，维持大的学习率所以更新较快。AdaGrad算法因为 S t S_{t} St 一直累加，导致学习率不断下降，在迭代后期可能由于学习率过小，更新缓慢。
2.6 RMSProp
RMSProp 解决了学习率不断减小，后期学习缓慢的问题。更新公式如下：
RMSProp将动量思想引入梯度的累加计算中，使用超参数 γ \gamma γ 控制当前梯度值与历史累加的梯度值各自所占的权重，每次只累加前面 S t S_{t} St 的部分值，这样就不会导致St一直累加增大，导致学习率一直下降的问题，比如某参数此次梯度值较小，那么 S t S_{t} St 对应位置的累加值也会缩小，不会一直增大。
RMSProp的缺陷：同AdaGrad，都只是解决了参数对应同一学习率的问题，就是将参数 x t x_{t} xt 更新公式中 g t g_{t} gt 前面的学习率改进为自适应学习率，并没有对梯度 g t g_{t} gt 进行改进, 丢弃了Momentum动量的做法，所以仍会出现loss曲线方向抖动的问题。
2.7 Adam
Adam同时考虑了自适应学习率以及动量梯度，是RMSProp和Momentum的结合，效果一般较好。参数更新公式如下：
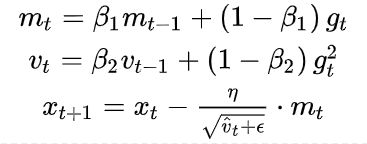m t m_{t} mt 是一阶动量的累加，保留了前一轮梯度方向信息的动量梯度，类似Momentum的做法； v t v_{t} vt 是二阶动量的累加，用于计算自适应学习率，类似于RMSProp的做法。更新参数 x t + 1 x_{t+1} xt+1 时同时使用动量梯度与自适应学习率，效果要优于之前的几种方法。
3 总结
梯度下降是贯穿机器学习与深度学习的经典优化算法，理解其原理才会在训练模型时得心应手的选择合适的梯度下降算法。下面做个对比总结以加深印象，避免混淆。
总结：
1>GD、SGD、mini-batch GD三者只在计算loss使用的样本数量上有差别，GD使用全部样本，SGD使用单个样本，mini-batch GD介于两者之间使用批量样本；
2>Momentum考虑了动量梯度，使得loss曲线没有那么曲折，但是存在参数共用一个学习率的缺陷；
3>AdaGrad与RMSProp引入了自适应学习率，让每个权重拥有自己的学习率。AdaGrad简单的累加梯度平方值会使得学习率不断变小，导致学习困难。RMSProp则在累加时加了相应的比例权重，防止梯度一直累加，解决了学习率一直减小的问题。但二者只考虑了自适应学习率，丢弃了Momentum动量梯度的做法；
4>Adam是Momentum与RMSProp的结合，使用动量方式来计算当前的梯度值，使用累加梯度平方来计算当前学习率，同时应用动量梯度与自适应学习率使得该算法效果优异。
梯度下降算法不只是这几种，这里只介绍了几种经典的算法，了解这些足以应付面试官了。
如果觉得有收获，就请点个赞吧~万分感谢！