NLP经典论文：Sequence to Sequence、Encoder-Decoder 、GRU 笔记

论文

NLP论文笔记合集（持续更新）

原论文：《Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine Translation》

最早的Sequence to Sequence模型：《Sequence to Sequence Learning with Neural Networks》

介绍

2014-06发表的文章，使用了Encoder-Decoder结构，解决了Sequence to Sequence输入长度和输出长度不对等的问题，并首次提出GRU结构。

特点

1. 使用了Encoder-Decoder结构，与RNN神经网络相比，解决了Sequence to Sequence输入长度和输出长度不对等的问题。对于长度为 n 或 m 的输入或输出，RNN神经网络只能解决 n to 1，1 to n 或 n to n 的情况，对 n to m 的问题很是头疼，Encoder-Decoder模型解决了n to m 的问题。Encoder使用RNN类的结构，将输入浓缩成固定长度的 context 向量，作为Decoder的输入，而Decoder中使用RNN类的结构，能够不断将每一次的输出值重新作为输入，再产生下一个输出。
2. 提出的GRU结构，比LSTM结构简单，效果相当。

模型结构

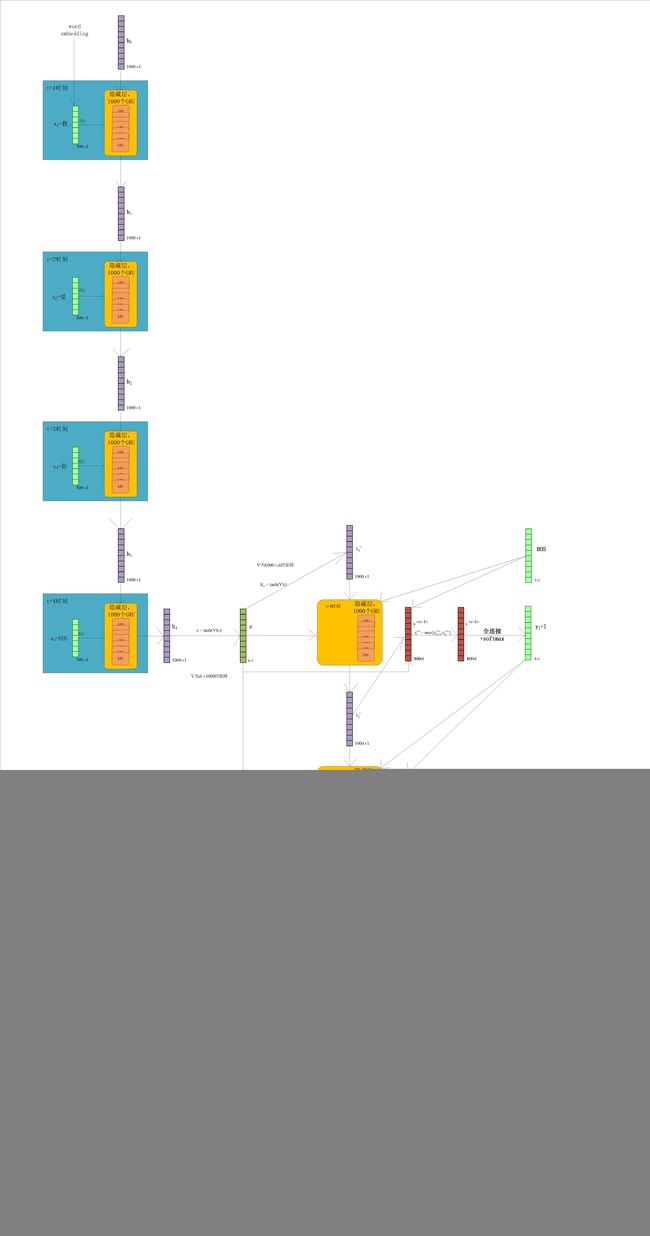
整体结构

输入

$X=({\mathbf{x}}_1,{\mathbf{x}}_2，\dots ,{\mathbf{x}}_T)$，$\mathbf{x}\in R^{d\times 1}$，$\mathbf{x}$为embedding表示的一个中文词，$X$为中文的一个句子，word embedding 矩阵共有 $K$ 个词，每个词用 $d$ 维向量表示。

输出

$Y=({\mathbf{y}}_1,{\mathbf{y}}_2，\dots ,{\mathbf{y}}_{T\prime })$，$\mathbf{y}\in R^{d\times 1}$，$\mathbf{y}$为embedding表示的一个英文词，$Y$为英文的一个句子，word embedding 矩阵共有 $K$ 个词，每个词用 $d$ 维向量表示。

整体流程

流程维度

GRU

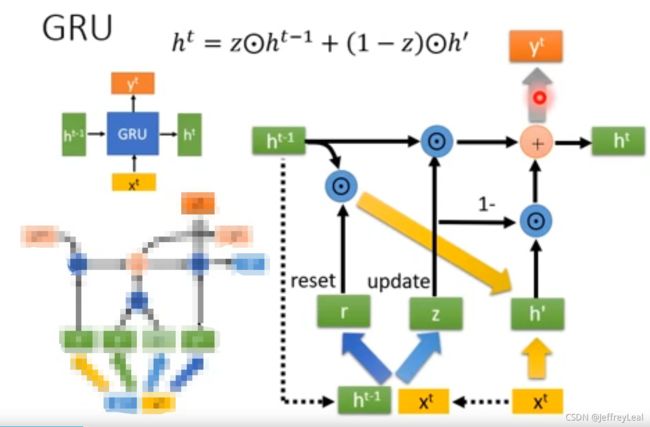
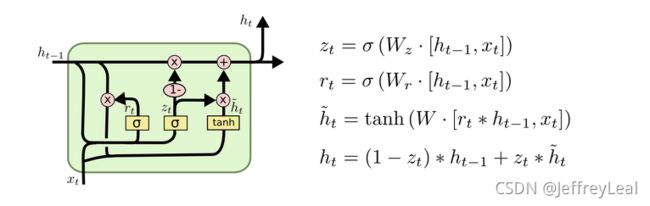
模型结构

GRU单元的理解

我们可以使用如下比喻：
$\mathbf{r}$：本能记忆遗忘系数，即过去记忆自热而然的遗忘速度，衰退系数；
$\mathbf{z}$：自主记忆保留系数，即自己选择记住多少东西
${\mathbf{h}}_{<t-1>}$：上一时刻的记忆，即过去的记忆
${\tilde{\mathbf{h}}}_j^{<t>}$：当前记忆的暂稳态，即刚吸收新知识的时候，新知识在大脑的记忆，是消化后的新知识，短期记忆
${\mathbf{h}}_{<t>}$：当前记忆的稳态，即吸收知识之后的总体记忆，吸收过去记忆与短期记忆后形成的长期记忆
$\mathbf{x}=(x_1,\dots ,x_T)$：新知识
$\mathbf{c}$：工作环境，创作背景，背景知识
$\mathbf{y}=(y_1,\dots ,y_{T\prime })$：作品

每一个隐藏单元是一个大脑。首先，本能记忆遗忘系数 $r_j$ 由以下公式计算：
$$r_j=\sigma ([{\mathbf{W}}_r\mathbf{x}{]}_j+[{\mathbf{U}}_r{\mathbf{h}}_{<t-1>}{]}_j),$$
可以看到，本能记忆遗忘系数 $\mathbf{r}$，是由新知识 $\mathbf{x}$ 和过去的记忆 ${\mathbf{h}}_{<t-1>}$ 决定的。也就是说，大脑在看到新知识之后，基于过去的记忆，可以计算出，对过去记忆自热而然的遗忘速度，这是机体的本能反应。

然后，通过以下公式计算提出的大脑当前时刻的短期记忆 ${\tilde{h}}_j^{<t>}$ ：
$${\tilde{h}}_j^{<t>}=\varphi ([\mathbf{W}\mathbf{x}{]}_j+[\mathbf{U}(\mathbf{r}\odot {\mathbf{h}}_{<t-1>}){]}_j).$$
可以看到，短期记忆 $\mathbf{h}$ 由新知识 $\mathbf{x}$ 、过去的记忆${\mathbf{h}}_{<t-1>}$ 和本能记忆遗忘系数 $r_j$ 决定的。也就是说，在大脑融合新知识和一部分过去的记忆成短期记忆，是新知识消化的过程，新知识在大脑中的反映。

类似地，自主记忆保留系数 $z_j$ 由以下公式计算：
$$z_j=\sigma ([{\mathbf{W}}_z\mathbf{x}{]}_j+[{\mathbf{U}}_z{\mathbf{h}}_{<t-1>}{]}_j).$$
可以看到，自主记忆保留系数 $\mathbf{z}$，是由新知识 $\mathbf{x}$ 和过去的记忆 ${\mathbf{h}}_{<t-1>}$ 决定的。也就是说，大脑在看到新知识之后，再对比过去的知识，自主选择对旧记忆的保留程度，这是非本能反应，是主动的选择。

最后，通过以下公式计算提出的大脑长期记忆 $h_j$ ：
$$h_j^{<t>}=z_j{h}_j^{<t-1>}+(1-z_j){\tilde{h}}_j^{<t>},$$
可以看到，当前长期记忆 ${\mathbf{h}}_{<t>}$ ，保留了一部分过去的记忆，以及筛选了一部分的短期记忆，融合两者形成长期记忆。

假如我们当前的任务是创作金庸风格的文章的话，当前创造词的条件分布是
$$p(y_t|y_{t-1}，y_{t-2}\dots ，y_1,\mathbf{c})=g({\mathbf{h}}_{<t>},y_{t-1},\mathbf{c})$$
可以看到，当前词的预测由当前的长期记忆 ${\mathbf{h}}_{<t>}$ 、上一个创作词 $y_{t-1}$ 和创作风格 $\mathbf{c}$。基于上一个创作词，按照当前的写作内容，写作能力，配合上金庸的创作风格，就能写出金庸风格的文章了。

Encoder

输入

$X=({\mathbf{x}}_1,{\mathbf{x}}_2，\dots ,{\mathbf{x}}_T)$，$\mathbf{x}\in R^{d\times 1}$，$\mathbf{x}$为embedding表示的一个中文词，$X$为中文的一个句子，word embedding 矩阵共有 $K$ 个词，每个词用 $d$ 维向量表示。

隐藏层

隐藏层共有1000个GRU单元。

对于RNN隐藏层来说，输入有$T$个词，就有$T$个输入时刻，每个时刻输入一个词。

t=1时刻

初始化hidden state ${\mathbf{h}}_{<0>}$，${\mathbf{h}}_{<t>}\in R^{1000\times 1}$，根据输入${\mathbf{x}}_1$，计算reset gate ${\mathbf{r}}_{<1>}$、update gate ${\mathbf{z}}_{<1>}$、短期记忆 ${\tilde{\mathbf{h}}}_{<1>}$、长期记忆 ${\mathbf{h}}_{<1>}$。

t时刻

根据输入${\mathbf{x}}_t$，上一时刻的记忆 ${\mathbf{h}}_{<t-1>}$，计算当前时刻的reset gate ${\mathbf{r}}_{<t>}$、update gate ${\mathbf{z}}_{<t>}$、短期记忆 ${\tilde{\mathbf{h}}}_{<t>}$、长期记忆 ${\mathbf{h}}_{<t>}$。
$${\mathbf{r}}_{<t>}=\sigma ({\mathbf{W}}_r\mathbf{x}+{\mathbf{U}}_r{\mathbf{h}}_{<t-1>}),$$$${\mathbf{z}}_{<t>}=\sigma ({\mathbf{W}}_z\mathbf{x}+{\mathbf{U}}_z{\mathbf{h}}_{<t-1>}),$$$${\tilde{\mathbf{h}}}_{<t>}=\varphi (\mathbf{W}\mathbf{x}+\mathbf{U}({\mathbf{r}}_{<t>}\odot {\mathbf{h}}_{<t-1>})),$$$${\mathbf{h}}_{<t>}={\mathbf{z}}_{<t>}\odot {\mathbf{h}}_{<t-1>}+(1-{\mathbf{z}}_{<t>})\odot {\tilde{\mathbf{h}}}_{<t>},$$
其中$\odot$代表2个向量在对应位置上元素相乘，$\sigma 、\varphi$ 分别表示 sigmoid 和 tanh 激活函数。${\mathbf{h}}_{<t-1>}$、$1$、${\mathbf{r}}_{<t>}$、${\mathbf{z}}_{<t>}$、${\tilde{\mathbf{h}}}_{<t>}$、${\mathbf{h}}_{<t>}\in R^{1000\times 1}$。${\mathbf{W}}_r、{\mathbf{W}}_z、\mathbf{W}\in R^{1000\times d}$。${\mathbf{U}}_r、{\mathbf{U}}_z、\mathbf{U}\in R^{1000\times 1000}$。

t=T时刻

RNN隐藏层经过 $T$ 个时刻的计算，最终得到${\mathbf{h}}_{<T>}$，经过下式计算，可得到上下文向量$\mathbf{c}$：
$$\mathbf{c}=tanh({\mathbf{V}\mathbf{h}}_{<T>}).$$
其中 $V\in R^{d_c\times 1000}，\mathbf{c}\in R^{d_c\times 1}$。$\mathbf{c}$ 包含了输入的全部信息。

Decoder

隐藏层也是有1000个GRU单元。

对于RNN隐藏层来说，输出有$T\prime$个词，每个时刻输出一个词。

t=1时刻

这里的 $t$ 时刻跟encoder的时刻不是同一时刻，而是encoder完成它的计算以后，decoder才开始自己的时序。

初始化hidden state ${\mathbf{h}}_{<0>}^{\prime }$：
$${\mathbf{h}}_{<0>}^{\prime }=tanh({\mathbf{V}}^{\prime }\mathbf{c}),$$
其中${\mathbf{V}}^{\prime }\in R^{1000\times d_c}$。

给予输出${\mathbf{y}}_0=BOS$，$BOS$ 为begin of sentence，句子起始符号，是输出的embedding中的词，与输入的embedding不是同一个，$\mathbf{y}\in R^{K\times 1}$。计算reset gate ${\mathbf{r}}_{<1>}^{\prime }$、update gate ${\mathbf{z}}_{<1>}^{\prime }$、短期记忆 ${\tilde{\mathbf{h}}}_{<1>}^{\prime }$、长期记忆 ${\mathbf{h}}_{<1>}^{\prime }$。

t时刻

GRU层

根据输入${\mathbf{y}}_{t-1}$，上一时刻的记忆 ${\mathbf{h}}_{<t-1>}^{\prime }$，计算当前时刻的reset gate ${\mathbf{r}}_{<t>}^{\prime }$、update gate ${\mathbf{z}}_{<t>}^{\prime }$、短期记忆 ${\tilde{\mathbf{h}}}_{<t>}^{\prime }$、长期记忆 ${\mathbf{h}}_{<t>}^{\prime }$。
$${\mathbf{r}}_{<t>}^{\prime }=\sigma ({\mathbf{W}}_r^{\prime }\mathbf{y}+{\mathbf{U}}_r^{\prime }{\mathbf{h}}_{<t-1>}^{\prime }+{\mathbf{C}}_r\mathbf{c}),$$$${\mathbf{z}}_{<t>}^{\prime }=\sigma ({\mathbf{W}}_z^{\prime }\mathbf{y}+{\mathbf{U}}_z^{\prime }{\mathbf{h}}_{<t-1>}^{\prime }+{\mathbf{C}}_z\mathbf{c}),$$$${\tilde{\mathbf{h}}}_{<t>}^{\prime }=\varphi ({\mathbf{W}}^{\prime }\mathbf{y}+{\mathbf{r}}_{<t>}^{\prime }\odot ({\mathbf{U}}^{\prime }{\mathbf{h}}_{<t-1>}^{\prime }+\mathbf{C}\mathbf{c})),$$$${\mathbf{h}}_{<t>}^{\prime }={\mathbf{z}}_{<t>}^{\prime }\odot {\mathbf{h}}_{<t-1>}^{\prime }+(1-{\mathbf{z}}_{<t>}^{\prime })\odot {\tilde{\mathbf{h}}}_{<t>}^{\prime },$$
其中$\odot$代表2个向量在对应位置上元素相乘，$\sigma 、\varphi$ 分别表示 sigmoid 和 tanh 激活函数。${\mathbf{h}}_{<t-1>}^{\prime }$、$1$、${\mathbf{r}}_{<t>}^{\prime }$、${\mathbf{z}}_{<t>}^{\prime }$、${\tilde{\mathbf{h}}}_{<t>}^{\prime }$、${\mathbf{h}}_{<t>}^{\prime }\in R^{1000\times 1}$。${\mathbf{W}}_r^{\prime }、{\mathbf{W}}_z^{\prime }、{\mathbf{W}}^{\prime }\in R^{1000\times d}$。${\mathbf{U}}_r^{\prime }、{\mathbf{U}}_z^{\prime }、{\mathbf{U}}^{\prime }\in R^{1000\times 1000}$。${\mathbf{C}}_r、{\mathbf{C}}_z、\mathbf{C}\in R^{1000\times d_c}$。

全连接层

将${\mathbf{h}}_{<t>}^{\prime }、{\mathbf{y}}_{t-1}、\mathbf{c}$传入全连接层：

$${\mathbf{s}}_{<t>}^{\prime }={\mathbf{O}}_h{\mathbf{h}}_{<t>}^{\prime }+{\mathbf{O}}_y{\mathbf{y}}_{t-1}+{\mathbf{O}}_c\mathbf{c}$$
其中，${\mathbf{O}}_h\in R^{2000\times 1000},{\mathbf{O}}_y\in R^{2000\times d},{\mathbf{O}}_c\in R^{2000\times d_c},{\mathbf{s}}_{<t>}^{\prime }\in R^{2000\times 1}$。

max pooling层

${\mathbf{s}}_{<t>}^{\prime }$经过 max pooling：

$$s_i^{<t>}=\max \{s_{2i-1}^{\prime <t>},s_{2i}^{\prime <t>}\}$$
$s_i^{<t>}$为${\mathbf{s}}_{<t>}$的第 $i$ 个词，${\mathbf{s}}_{<t>}\in R^{1000\times 1}$。

全连接层+softmax层

最后${\mathbf{s}}_{<t>}$传入全连接层+softmax，预测为字典里面第 $j$ 个词的概率为：
$$p({\mathbf{y}}_{t,j}=1|{\mathbf{y}}_{t-1},...,{\mathbf{y}}_1,\mathbf{X})=\frac{exp({\mathbf{g}}_j{\mathbf{s}}_{<t>})}{\sum _{j\prime =1}^{K}exp({\mathbf{g}}_{j\prime }{\mathbf{s}}_{<t>})}$$
其中$\mathbf{g}\in \mathbf{G},\mathbf{G}\in R^{K\times 1000}$。

得到预测词 ${\mathbf{y}}_t$。

t=T’时刻

RNN隐藏层经过 $T\prime$ 个时刻的计算，最终得到$Y=({\mathbf{y}}_1,{\mathbf{y}}_2，\dots ,{\mathbf{y}}_{T\prime })$。

文章部分翻译

2 RNN Encoder–Decoder

2.1 Preliminary: Recurrent Neural Networks

循环神经网络（RNN）是由隐藏状态$\mathbf{h}$和可选输出$\mathbf{y}$组成的神经网络，该输出$\mathbf{y}$在可变长度序列$\mathbf{x}=（x_1，\dots ，x_T）$上进行计算。在每个时间步 $t$，RNN的隐藏状态${\mathbf{h}}_{<h>}$的更新由
$${\mathbf{h}}_{<t>}=f({\mathbf{h}}_{<t-1>},x_t),(1)$$
其中$f$是一个非线性激活函数。$f$可以像logistic sigmoid函数一样简单，其中sigmoid的参数与输入元素数量相匹配，也可以像长短时记忆（LSTM）单元一样复杂（Hochreiter和Schmidhuber，1997）。

RNN可以通过训练如何预测序列中的下一个symbol来学习序列的概率分布。那样的话，每个时间步 $t$ 的输出是条件分布$p(x_t|x_{t-1},\dots ,x_1)$。例如，输出多项式分布（1-of-K coding，one-hot）可以通过softmax激活函数得到
$$p(x_{t,j}=1|x_{t-1},...,x_1)=\frac{exp({\mathbf{w}}_j{\mathbf{h}}_{<t>})}{\sum _{j\prime =1}^{V}exp({\mathbf{w}}_{j\prime }{\mathbf{h}}_{<t>})}$$
对于所有可能的$j=1,...,K$， 其中${\mathbf{w}}_j$是权重矩阵$\mathbf{W}$的行。通过组合这些概率，我们可以计算可能的序列$\mathbf{x}$通过
$$p(\mathbf{x})=\prod _{t=1}^{T}p(x_t|x_{t-1},\dots ,x_1)(3)$$

按照这种分布，可以直接通过在每个时间步对一个symbol进行迭代采样，来对新序列进行采样。

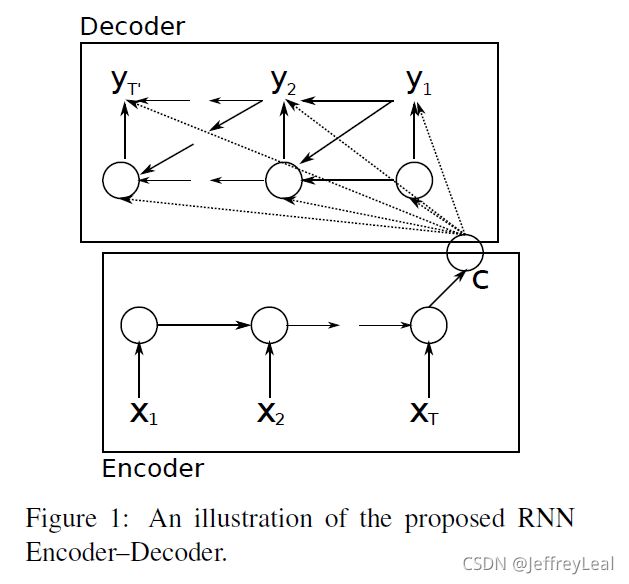
2.2 RNN Encoder–Decoder

在本文中，我们提出了一种新的神经网络结构，该结构学习如何将可变长度序列编码为固定长度向量，并将给定的固定长度向量解码回可变长度序列。从概率的角度来看，这个新模型是一种学习变长序列在另一个变长序列上的条件分布的通用方法，例如$p(y_1，\dots ，y_T\prime |x_1，\dots ，x_T)$，其中应注意输入和输出序列长度$T$和$T\prime$可能会有所不同。

编码器是一个RNN，按顺序读取输入序列$\mathbf{x}$的每个symbol。当它读取每个symbol时，RNN的隐藏状态根据等式（1）改变。读取序列末尾（由序列末尾符号标记）后，RNN的隐藏状态是整个输入序列的摘要$c$。

该模型的解码器是另一个RNN，该RNN经过训练，通过给定的隐藏状态${\mathbf{h}}_{<t>}$预测下一个symbol $y_t$来生成输出序列。但是，与第2.1节中描述的RNN不同，$y_t$和${\mathbf{h}}_{<t>}$还基于条件$y_{t-1}$和输入序列的摘要$\mathbf{c}$。因此，解码器在时间t的隐藏状态通过以下公式计算：
$${\mathbf{h}}_{<t>}=f({\mathbf{h}}_{<t-1>},y_{t-1},\mathbf{c}),$$
同样，下一个symbol的条件分布是
$$p(y_t|y_{t-1}，y_{t-2}\dots ，y_1,\mathbf{c})=g({\mathbf{h}}_{<t>},y_{t-1},\mathbf{c})$$
对于给定的激活函数$f$和$g$（后者必须产生有效概率，例如，使用softmax）。

请参考图1，以获取提出的模型架构的图形描述。

提出的RNN Encoder–Decoder的两个组件被联合训练以最大化条件对数似然
$$\underset{\theta }{\max }\frac{1}{N}\sum _{n=1}^N\log p_{\theta }({\mathbf{y}}_n|{\mathbf{x}}_n),(4)$$
其中$\theta$是模型参数集，每个$({\mathbf{x}}_n,{\mathbf{y}}_n)$是训练集中的对（输入序列，输出序列）。在我们的例子中，由于解码器的输出（从输入开始）是可微的，我们可以使用基于梯度的算法来估计模型参数。

一旦对RNN编码器-解码器进行了训练，该模型可用于两种方式。一种方法是给定输入序列，使用模型生成的目标序列。另一方面，该模型可用于对给定的一对输入和输出序列进行评分，其中评分仅为等式（3）和（4）中的概率$p_{\theta }(\mathbf{y}|\mathbf{x})$。

2.3 Hidden Unit that Adaptively Remembers and Forgets

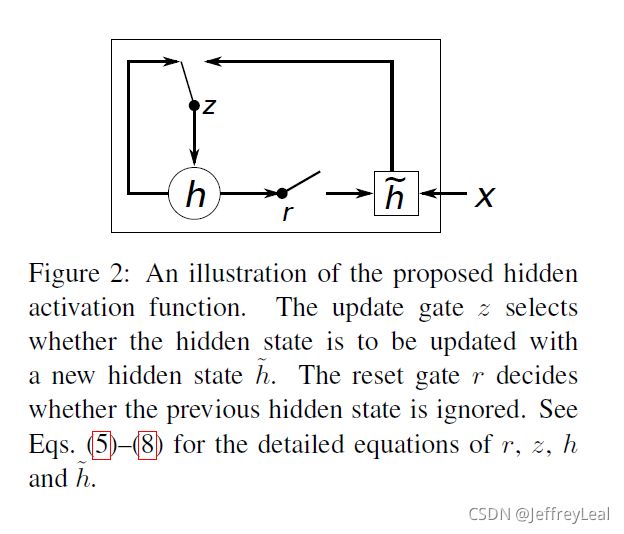
除了一种新颖的模型架构外，我们还提出了一种新型的隐藏单元（式（1）中的$f$），该隐藏单元源自LSTM单元，但计算和实现起来要简单得多。图2展示了所提出的隐藏单元的图形描述。

让我们描述如何计算第$j$个隐藏单元的激活。首先，重置门$r_j$由以下公式计算：
$$r_j=\sigma ([{\mathbf{W}}_r\mathbf{x}{]}_j+[{\mathbf{U}}_r{\mathbf{h}}_{<t-1>}{]}_j),(5)$$
其中$\sigma$是logistic sigmoid函数，$[.{]}_j$表示向量的第j个元素。$\mathbf{x}$和${\mathbf{h}}_{<t-1>}$分别是输入和先前的隐藏状态。${\mathbf{W}}_r$和${\mathbf{U}}_r$是习得的权重矩阵。

类似地，更新门$z_j$由以下公式计算：
$$z_j=\sigma ([{\mathbf{W}}_z\mathbf{x}{]}_j+[{\mathbf{U}}_z{\mathbf{h}}_{<t-1>}{]}_j).(6)$$
然后，通过以下公式计算提出的单元$h_j$的实际激活：
$$h_j^{<t>}=z_j{h}_j^{<t-1>}+(1-z_j){\tilde{h}}_j^{<t>},(7)$$
其中
$${\tilde{h}}_j^{<t>}=\varphi ([\mathbf{W}\mathbf{x}{]}_j+[\mathbf{U}(\mathbf{r}\odot {\mathbf{h}}_{<t-1>}){]}_j).(8)$$
在此公式中，当重置门接近0时，隐藏状态被强制忽略先前的隐藏状态，并仅使用当前输入重置。这有效地使得隐藏状态删除以后发现的任何不相关信息，从而得到更紧凑的表示。

另一方面，更新门控制多少信息量会从先前的隐藏状态带到当前的隐藏状态。这类似于LSTM网络中的存储单元，有助于RNN记住长期信息。此外，这可能被视为leaky-integration unit的adaptive variant （Bengio等人，2013年）。

由于每个隐藏单元都有单独的重置和更新门，因此每个隐藏单元将学习捕获不同时间尺度上的依赖关系。那些学习捕捉短期依赖关系的单元往往具有经常处于活动状态的重置门，但那些捕捉长期依赖关系的单元将具有大部分处于活动状态的更新门。

在我们的初步实验中，我们发现使用这种有门控的新单元是至关重要的。我们使用常用的无门控tanh单位无法得到有意义的结果。

3 Statistical Machine Translation

在一个常用的统计机器翻译系统（SMT）中，系统（特别是译码器）的目标是给定源语句$\mathbf{e}$，找到的翻译$\mathbf{f}$，从而最大化
$$p(\mathbf{f}|\mathbf{e})\propto p(\mathbf{e}|\mathbf{f})p(\mathbf{f}),$$
其中，右侧的第一项称为翻译模型，后一项称为语言模型（参见，例如，（Koehn，2005））。然而，在实践中，大多数SMT系统将对数p（f | e）建模为具有附加特征和相应权重的对数线性模型：
$$\log p(\mathbf{f}|\mathbf{e})=\sum _{n=1}^N{w}_n{f}_n(\mathbf{f},\mathbf{e})+\log Z(\mathbf{e}),(9)$$
其中$f_n$和$w_n$分别是第$n$个特征和权重。$Z(\mathbf{e})$是不依赖于权重的归一化常数。权重通常以最大化验证集上的BLEU分数来进行优化。在（Koehn等人，2003年）和（Marcu和Wong，2002年）介绍的基于短语的SMT框架中，翻译模型$\log p(\mathbf{f}|\mathbf{e})$被分解为匹配源句子中的短语和目标句子中的短语的翻译概率。在对数线性模型中，这些概率再次被视为附加特征（见等式（9）），并相应地进行加权，以最大化BLEU分数。

自（Bengio等人，2003年）提出神经网络语言模型以来，神经网络已广泛应用于SMT系统。在许多情况下，神经网络被用来重新审视翻译模型的假设（n-最佳列表）（参见，例如，（Schwenk等人，2006））。然而最近，训练神经网络以使用源句子（或短语对）的表示作为额外的输入来对翻译句子进行评分引起了广泛的兴趣。例如，见（Schwenk，2012），（Son等人，2012）和（Zou等人，2013）。

3.1 Scoring Phrase Pairs with RNN Encoder–Decoder

在这里，我们建议在短语对照表上训练RNN编码器-解码器（见第2.2节），并在调整SMT解码器时，将其分数用作等式（9）中对数线性模型的附加特征。

当我们训练RNN编码器-解码器时，我们忽略原始语料库中每个短语对的（标准化）频率。采取这一措施的目的是：（1）减少从大型短语表中根据归一化频率随机选择短语对的计算花费；（2）确保RNN编码器-解码器不会根据短语对的出现次数简单地学习对短语进行排序。这种选择的一个根本原因是短语表中现有的翻译概率已经反映了原始语料库中短语对的频率。对于RNN编码器-解码器的固定容量，我们试图确保模型的大部分容量集中于学习语言规律，即区分似是而非的翻译，或学习似是而非翻译的“复杂多变体”（概率集中区域）。

一旦RNN编码器-解码器经过训练，我们将为每个短语对添加一个新的分数到现有短语表中。这使得新的分数加入到现有的优化算法，而计算的额外开销最小。

正如Schwenk在（Schwenk，2012）中指出的那样，可以用提出的RNN编码器-解码器完全替换现有短语表。在这种情况下，对于给定的源短语，RNN编码器-解码器将需要生成（好的）目标短语列表。然而，这需要重复执行计算量巨大的取样步骤。因此，本文只考虑短语表中短语对的重新排序问题。

3.2 Related Approaches: Neural Networks in Machine Translation

在给出实证结果之前，我们讨论了一些最近提出在SMT环境下使用神经网络的工作。

Schwenk in（Schwenk，2012）提出了一种类似的短语对评分方法。他没有使用基于RNN的神经网络，而是使用了一个前馈神经网络，该网络具有固定大小的输入（在他的例子中为7个单词，较短短语为零填充）和固定大小的输出（目标语言中为7个单词）。当它专门用于SMT系统的短语评分时，最大短语长度通常选择较小。然而，随着短语长度的增加，或者当我们将神经网络应用于其他可变长度序列数据时，神经网络能够处理可变长度的输入和输出是很重要的。提出的RNN编码器-解码器非常适合这些应用。

与（Schwenk，2012）类似，Devlin等人（Devlin等人，2014）提出使用前馈神经网络对翻译模型建模，但每次预测目标短语中的一个单词。他们提出了一个令人印象深刻的改进，但他们的方法仍然要求输入短语（或上下文词）的最大长度事先固定。

虽然这并不完全是他们训练的神经网络，但（Zou等人，2013年）的作者提出学习双语单词/短语的embedding。他们使用学习到的embedding来计算短语对之间的距离，该距离在SMT系统中用作短语对的附加分数。

在（Chandar等人，2014年）中，对前馈神经网络进行了训练，以学习词袋表示的输入短语到输出短语的映射。这与提出的RNN编码器-解码器和（Schwenk，2012）中提出的模型密切相关，只是它们对短语的输入表示是词袋模型的表示。在（Gao等人，2013年）中也提出了使用词袋表示的类似方法。早些时候，在（Socher et al.，2011）中提出了使用两个递归神经网络的类似编码器-解码器模型，但其模型仅限于单语设置，即该模型重构输入句子。最近，在（Auli et al.，2013）中提出了另一种使用RNN的编码器-解码器模型，其中解码器以源语句或源上下文的表示为条件。

提出的RNN编码器-解码器与（Zou等人，2013年）和（Chandar等人，2014年）中的方法之间的一个重要区别是，考虑了源短语和目标短语中单词的顺序。RNN编码器-解码器自然地区分具有相同单词但顺序不同的序列，而上述方法有效地忽略了顺序信息。

与提出的RNN编码器-解码器相关的最接近的方法是（Kalchbrenner和Blunsom，2013）中提出的循环连续翻译模型（模型2）。在他们的论文中，他们提出了一个由编码器和解码器组成的类似模型。与我们的模型不同的是，他们使用卷积n-gram模型（CGM）作为编码器，使用逆CGM和循环神经网络的混合作为解码器。然而，他们评估了他们的模型，重新审视了传统SMT系统提出的n-最佳列表，并计算了黄金标准翻译的复杂性。

4 Experiments

我们评估了WMT’14研讨会英语/法语翻译任务的方法。

4.4 Word and Phrase Representations

由于所提出的RNN编码器-解码器并不是专门为机器翻译任务而设计的，这里我们简要介绍一下训练模型的特性。

一段时间以来，人们已经知道，使用神经网络的连续空间语言模型能够学习语义上有意义的embedding（参见，例如，（Bengio et al.，2003；Mikolov et al.，2013））。由于所提出的RNN编码器-解码器也投射到一个单词序列并从该序列映射回一个连续的空间向量，因此我们期望所提出的模型也具有类似的特性。

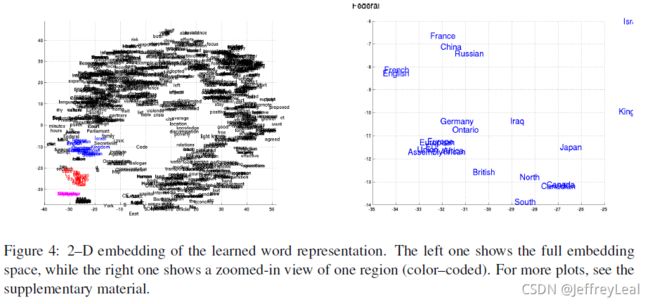
图4中的左图显示了使用RNN编码器-解码器学习的词嵌入矩阵对单词进行的2-D的 embedding。该映射由最近提出的Barnes Hut SNE（van der Maaten，2013）完成。我们可以清楚地看到语义相似的单词彼此聚集在一起（参见图4中的放大图）。

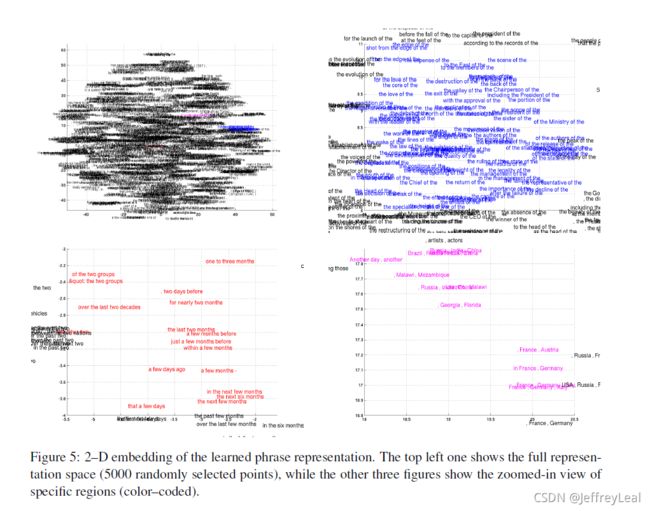
提出的RNN编码器-解码器自然生成短语的连续空间表示。这种情况下的表示（图1中的c）是1000维向量。与单词表示类似，我们使用图5中的Barnes-Hut SNE可视化表示由四个或更多单词组成的短语。

从可视化的角度来看，RNN编码器-解码器可以捕获短语的语义和句法结构。例如，在左下角的图中，大多数短语都与时间长短有关，而那些语法相似的短语则聚集在一起。右下角的图显示了语义相似的短语集群（国家或地区）。另一方面，右上角的图显示了语法相似的短语。

4.1 Data and Baseline System

4.1.1 RNN Encoder–Decoder

A RNN Encoder–Decoder

在本文中，我们详细描述了实验中使用的RNN编码器-解码器的体系结构。

让我们用$X=({\mathbf{x}}_1,{\mathbf{x}}_2，\dots ,{\mathbf{x}}_N)$表示源短语，用$Y=({\mathbf{y}}_1,{\mathbf{y}}_2，\dots ,{\mathbf{y}}_M)$表示目标短语。每个短语是$K$维one-hot向量的序列，向量中只有一个元素为1，所有其他元素为0。非零元素（1）的索引指示由向量表示的单词。

(注：感觉这里的$X$是应该是一个句子，不过短语和句子其实本质上是一样的，$({\mathbf{x}}_1,{\mathbf{x}}_2，\dots ,{\mathbf{x}}_N)$是句子里面的词，每一个词${\mathbf{x}}_i$用$K$维one-hot向量表示）

A.1 Encoder

源短语的每个单词都嵌入到500维向量空间中：$e({\mathbf{x}}_i)\in R^{500}$。$e(\mathbf{x})$在第4.4节中用于将单词形象化。

编码器的隐藏状态由1000个隐藏单元组成，在时刻 $t$，每个隐藏单元的计算公式为
$$h_j^{<t>}=z_j{h}_j^{<t-1>}+(1-z_j){\tilde{h}}_j^{<t>},$$
其中
$${\tilde{h}}_j^{<t>}=tanh([\mathbf{W}e({\mathbf{x}}_t){]}_j+[\mathbf{U}(\mathbf{r}\odot {\mathbf{h}}_{<t-1>}){]}_j),$$$$z_j=\sigma ([{\mathbf{W}}_{z}e({\mathbf{x}}_t){]}_j+[{\mathbf{U}}_z{\mathbf{h}}_{<t-1>}{]}_j),$$$$r_j=\sigma ([{\mathbf{W}}_{r}e({\mathbf{x}}_t){]}_j+[{\mathbf{U}}_r{\mathbf{h}}_{<t-1>}{]}_j).$$
$\sigma$和$\odot$分别是logistic sigmoid函数和元素乘法。为了使方程更清晰，我们省略了偏差。初始隐态$h_j^{<0>}$固定为0。

一旦计算了$N$步（源短语的结尾）处的隐藏状态，则源短语 $\mathbf{c}$ 的表示为
$$\mathbf{c}=tanh({\mathbf{V}\mathbf{h}}^{<N>}).$$

A.1.1 Decoder

解码器首先使用初始化隐藏状态
$$h^{\prime <0>}=tanh({\mathbf{V}}^{\prime }\mathbf{c}),$$
其中我们将使用${\cdot }^{\prime }$区分解码器和编码器的参数。

解码器在时间 $t$ 的隐藏状态由以下公式计算：
$$h_j^{\prime <t>}=z_j^{\prime }{h}_j^{\prime <t-1>}+(1-z_j^{\prime }){\tilde{h}}_j^{\prime <t>},$$
其中
$${\tilde{h}}_j^{\prime <t>}=tanh([{\mathbf{W}}^{\prime }e({\mathbf{y}}_{t-1}){]}_j+r_j^{\prime }[{\mathbf{U}}^{\prime }{\mathbf{h}}_{<t-1>}^{\prime }+\mathbf{C}\mathbf{c}{]}_j),$$$$z_j^{\prime }=\sigma ([{\mathbf{W}}_z^{\prime }e({\mathbf{y}}_{t-1}){]}_j+[{\mathbf{U}}_z^{\prime }{\mathbf{h}}_{<t-1>}^{\prime }{]}_j+[{\mathbf{C}}_z\mathbf{c}{]}_j),$$$$r_j^{\prime }=\sigma ([{\mathbf{W}}_r^{\prime }e({\mathbf{y}}_{t-1}){]}_j+[{\mathbf{U}}_r^{\prime }{\mathbf{h}}_{<t-1>}^{\prime }{]}_j+[{\mathbf{C}}_r\mathbf{c}{]}_j).$$
$e({\mathbf{y}}_0)$是一个全零向量。与编码器的情况类似，$e(\mathbf{y})$是目标字的embedding。

与只编码源短语的编码器不同，解码器学习生成目标短语。在每个时间 $t$，解码器通过以下方式计算生成第 $j$ 个字的概率：
$$p(y_{t,j}=1|{\mathbf{y}}_{t-1},...,{\mathbf{y}}_1,\mathbf{X})=\frac{exp({\mathbf{g}}_j{\mathbf{s}}_{<t>})}{\sum _{j\prime =1}^{K}exp({\mathbf{g}}_{j\prime }{\mathbf{s}}_{<t>})}$$
其中${\mathbf{s}}_{<t>}$的第 $i$ 个元素是
$$s_i^{<t>}=\max \{s_{2i-1}^{\prime <t>},s_{2i}^{\prime <t>}\}$$
并且
$${\mathbf{s}}^{\prime <t>}={\mathbf{O}}_h{\mathbf{h}}^{\prime <t>}+{\mathbf{O}}_y{\mathbf{y}}_{t-1}+{\mathbf{O}}_c\mathbf{c}$$
简单来说，$s_i^{<t>}$是所谓的最大输出单元。

为了提高计算效率，不使用单个矩阵输出权重 $\mathbf{G}$，我们使用两个矩阵的乘积
$$\mathbf{G}={\mathbf{G}}_l{\mathbf{G}}_r$$
其中${\mathbf{G}}_l\in R^{K\times 500}$和${\mathbf{G}}_r\in R^{500\times 1000}$

B Word and Phrase Representations

这里，我们展示了单词和短语表示的放大图，在图4–5中。

相关视频

Sequence-to-sequence Learning

相关笔记

论文笔记：GRU、Encoder-Decoder
详解从 Seq2Seq模型、RNN结构、Encoder-Decoder模型 到 Attention模型
Understanding LSTM Networks

相关复现

pytorch

bentrevett/pytorch-seq2seq

tensorflow

keras

API

pytorch API:

GRU

tensorflow API