[论文解读]Fast-Tracker:在复杂环境中敏捷跟踪目标的鲁棒性空中系统
标题:Fast-Tracker: A Robust Aerial System for Tracking Agile
Target in Cluttered Environments
作者:Zhichao Han*, Ruibin Zhang*, Neng Pan*, Chao Xu, and Fei Gao
来源:https://arxiv.org/pdf/2011.03968v1.pdf
代码:https://github.com/ZJU-FAST-Lab/Fast-tracker
文章目录
- 摘要
- 主要贡献
- 一、原理
-
- 1.目标未知的运动预测
-
- 1.1 带约束的贝塞尔预测轨迹
- 1.2 目标重定位
- 2.安全的轨迹跟踪规划
-
- 2.1 目标导向的运动学跟踪路径搜索
- 2.1.1 邻节点扩展
- 2.1.2 损失函数
- 2.2 最优时空轨迹生成
- 二、实验结果
-
- 1. 实验平台
- 2. 实际场景测试
- 三、总结
摘要
本文提出了一种在无人机在目标行动和稠密环境未知的情况,实现自主敏捷跟踪目标的系统方案。
我们的工作主要分为两个部分:目标运动预测和跟踪轨迹规划。
- 目标运动预测:利用目标历史的观测值信息,在考虑目标动态约束的情况下预测目标的未来运动轨迹。
- 跟踪轨迹规划器:传统的规划结构。前端采用考虑运动学的搜索方法,通过启发式的方法搜索出一条安全的跟踪轨迹。后端优化器将其优化为时空最优且无碰撞的轨迹。
主要贡献
- 目标运动未知情况下基于贝塞尔多面体约束的轻量级运动预测方法;
- 一个安全的跟踪轨迹规划器,包括考虑目标的运动学搜索前端规划器和基于时空最优的轨迹规划后端优化器。
- 集成感知功能的系统解决方案,并进行广泛评估。
![[论文解读]Fast-Tracker:在复杂环境中敏捷跟踪目标的鲁棒性空中系统_第1张图片](http://img.e-com-net.com/image/info8/b6262b54027f4e639e3f75e8bc5ea5c2.jpg)
![[论文解读]Fast-Tracker:在复杂环境中敏捷跟踪目标的鲁棒性空中系统_第2张图片](http://img.e-com-net.com/image/info8/a4b1d1f3d693445689186256f6596fe2.jpg)
一、原理
1.目标未知的运动预测
1.1 带约束的贝塞尔预测轨迹
我们利用伯恩斯坦基础多项式(称为贝塞尔曲线)来描述目标的预测轨迹。 n阶贝塞尔曲线表示为:
![[论文解读]Fast-Tracker:在复杂环境中敏捷跟踪目标的鲁棒性空中系统_第3张图片](http://img.e-com-net.com/image/info8/82069d6742854417b8cd94947ac94d28.jpg)
其中每个 b n i b^i_n bni是一个n阶Bernstein多项式,[ c 0 c_0 c0, c 1 c_1 c1,…, c n c_n cn]是贝塞尔曲线的控制点集合。
我们将观测到的处于世界坐标下目标的位置和时间戳加入到一个长度为L的FIFO队列。该队列表示为 Q t a r g e t Q_{target} Qtarget = [ q 1 q_1 q1, q 2 q_2 q2,…, q L q_L qL],其中 q i q_i qi = { p t i p_{t_i} pti, t i t_i ti}。 Q t a r g e t Q_{target} Qtarget包含的时间范围为[ t 1 t_1 t1, t L t_L tL],其中 t L t_L tL表示的是当前时间。当获得新的目标观测值时,\拟合过去的观测值来生成新的目标预测轨迹 B ^ ( t ) \hat{B}(t) B^(t)。 预测时间范围为( t L t_L tL, t p t_p tp],在该段时间内我们来预测目标运动,所提出的目标运动预测方法如图3所示。
![[论文解读]Fast-Tracker:在复杂环境中敏捷跟踪目标的鲁棒性空中系统_第4张图片](http://img.e-com-net.com/image/info8/43f37013480940c78b9caf6a926ddd99.jpg)
过去的观测结果可信度会随着时间的流逝而降低,观测值越靠前,在损失函数中所占权重就越低。我们选择添加权重 w t i w_{t_i} wti来区分不同时间的置信度。使用双曲线 t a n tan tan h ( x ) h(x) h(x)计算权重:
![[论文解读]Fast-Tracker:在复杂环境中敏捷跟踪目标的鲁棒性空中系统_第5张图片](http://img.e-com-net.com/image/info8/6c1e43f3066246bb931d92aeef256026.jpg)
当 t i t_i ti与当前时间 t L t_L tL之间的时间差增大时,其函数值会迅速减小,从而可以有效地区分不同观测值的置信度。
整体损失函数设计如下:
![[论文解读]Fast-Tracker:在复杂环境中敏捷跟踪目标的鲁棒性空中系统_第6张图片](http://img.e-com-net.com/image/info8/9de0298446d7461ab3f3e237476c996b.jpg)
损失函数包含两部分,第一部分是为了尽可能减少目标轨迹和观测值之间的距离残差,第二部分是添加了二阶正交项以避免过度拟合。 w p w_p wp代表权重值。
为了确保目标预测轨迹的动力学可行性,需要将预测速度和加速度约束在[- v m p v_{mp} vmp, v m p v_{mp} vmp]和[- a m p a_{mp} amp, a m p a_{mp} amp]中。 由于贝塞尔曲线´的凸包性和hodograph性,我们只需要在x,y,z之外的一维µ上对每个控制点 c i c_i ci施加以下约束:
![[论文解读]Fast-Tracker:在复杂环境中敏捷跟踪目标的鲁棒性空中系统_第7张图片](http://img.e-com-net.com/image/info8/306ac93908cd41eb93c5b990b655f2a9.jpg) 其中,n是贝塞尔曲线的阶数,st是时间比例因子。
其中,n是贝塞尔曲线的阶数,st是时间比例因子。
贝塞尔曲线二范数正定,所以目标预测问题是带约束的QP问题。 我们使用OOQP来构建和解决所提出带约束的贝塞尔回归问题。
1.2 目标重定位
无人机在失去目标观测值的情况下应该采取有效的策略主动探索并重新定位目标。在多数情况下,无人机可以快速到达目标最后的观测位置,并沿着目标预测轨迹来重新定位目标,具体步骤如下:
1)首先,通过路径搜索算法来获得起点(无人机的当前位置)与目的地(最后的目标观测值)之间的最短安全路径 p o b s p_{obs} pobs。然后,离散化最后一段的目标预测轨迹。若预测轨迹会撞上障碍物,则利用局部路径搜索算法来生成无碰撞路径 p p r e p_{pre} ppre。将 p o b s p_{obs} pobs和 p p r e p_{pre} ppre进行连接为完整的重定位路径 p r p_r pr;
2)基于 p r p_r pr生成飞行走廊;
3)在飞行走廊内生成时空最优且无碰撞的轨迹作为最终的重新定位轨迹;
4)在重新定位过程中,如果沿着重新定位轨迹观察到新的障碍物,则会生成一条新的安全轨迹。
![[论文解读]Fast-Tracker:在复杂环境中敏捷跟踪目标的鲁棒性空中系统_第8张图片](http://img.e-com-net.com/image/info8/73b911eedfda4888bd97fb0c6ae61b73.jpg)
2.安全的轨迹跟踪规划
2.1 目标导向的运动学跟踪路径搜索
运动学搜索方法是基于混合A *算法,该算法通过离散化控制输入来扩展生成节点(运动原语),可以在体素网格图中搜索出安全且动力学可行的轨迹。方法包含邻节点的扩展和启发式函数设计,算法框架如下:
![[论文解读]Fast-Tracker:在复杂环境中敏捷跟踪目标的鲁棒性空中系统_第9张图片](http://img.e-com-net.com/image/info8/56855e6a518e4220a3ddcea08fa4c74c.jpg)
![[论文解读]Fast-Tracker:在复杂环境中敏捷跟踪目标的鲁棒性空中系统_第10张图片](http://img.e-com-net.com/image/info8/28d9709219b44c69badc4d35bbef9e4b.jpg)
2.1.1 邻节点扩展
无人机状态向量表示为:x = ( p x , p y , p z , v x , v y , v z ) T (p_x, p_y, p_z,v_x, v_y, v_z)^T (px,py,pz,vx,vy,vz)T
控制输入:加速度 u u u,令 u u u ∈ U U U:= [- a m t a_{mt} amt, a m t a_{mt} amt ] ⊂ R 3 R^3 R3
我们统一用 u D u_D uD来表示离散的 u u u序列:= {- a m t a_{mt} amt, − n a − 1 n a a m t -\frac {n_a - 1}{n_a}a_{mt} −nana−1amt, … , n a − 1 n a a m t \frac {n_a - 1}{n_a}a_{mt} nana−1amt, a m t a_{mt} amt },时间序列 Δ T \Delta T ΔT表示为{ 1 n t Δ T m \frac {1}{n_t}\Delta T_m nt1ΔTm, 2 n t Δ T m \frac {2}{n_t}\Delta T_m nt2ΔTm, …, n t − 1 n t Δ T m \frac {n_t - 1}{n_t}\Delta T_m ntnt−1ΔTm, Δ T \Delta T ΔT }。该状态方程可以表示为:![[论文解读]Fast-Tracker:在复杂环境中敏捷跟踪目标的鲁棒性空中系统_第11张图片](http://img.e-com-net.com/image/info8/b139258236c64622b91aebf8d27cd7be.jpg)
其中 X k − 1 X_{k-1} Xk−1表示之前的状态,给出 X k − 1 X_{k-1} Xk−1, u D u_D uD, Δ T \Delta T ΔT可以得到基于运动学的扩展节点。每次扩展都能生成 ( 2 n a + 1 ) 3 . n t (2n_a + 1)^3.n_t (2na+1)3.nt个节点。
2.1.2 损失函数
节点的损失函数表示为 f c = g c + h c f_c = g_c + h_c fc=gc+hc。 g c g_c gc表示从初始状态 x 0 x_0 x0到当前状态 x c x_c xc的实际代价,而 h c h_c hc表示用于快速搜索的启发式代价。
首先介绍 f c f_c fc部分,为了权衡控制效果和轨迹的时间,我们将能量-时间代价最小化为:

在每次扩展节点的时候,输入离散的 u D u_D uD和 Δ T \Delta T ΔT表示为 e c = ( ∣ ∣ u D ∣ ∣ 2 + ρ ) Δ T e_c = (||u_D||^2 + \rho ) \Delta T ec=(∣∣uD∣∣2+ρ)ΔT,根据该定义,如果到 x c x_c xc的最佳路径 x 0 x_0 x0包含m个运动原语,则 g c g_c gc可以表示为:
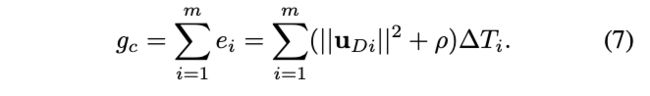
启发式函数 h c h_c hc分为两部分:

距离损失函数 D ( X c , X g ) D(X_c, X_g ) D(Xc,Xg):无人机当前状态 X c X_c Xc到目状态 X g X_g Xg的距离。
目标状态 x g x_g xg:由跟踪目标的当前状态 X t c X_{tc} Xtc和预测t时刻后状态 X t p X_{tp} Xtp的中间量得到。

其中 φ φ φ表示权重。
预测状态 X t p X_{tp} Xtp:有预测轨迹 B ^ ( t ) \hat{B}(t) B^(t)得出,速度量是 B ^ ( t ) \hat{B}(t) B^(t)的一阶导数, X t p ( t ) X_{tp}(t) Xtp(t) = { P t p , V t p P_{tp}, V_{tp} Ptp,Vtp} = { B ^ ( t ) , B ^ ( 1 ) ( t ) \hat{B}(t), \hat{B}^{(1)}(t) B^(t),B^(1)(t)}。其中 D ( X c , X g ) D(X_c, X_g ) D(Xc,Xg)采用 X c X_c Xc到 X g X_g Xg的OBVP距离,转换为两点边界值问题(BVP),用于求解最小化动态损失函数的最优路径。
![[论文解读]Fast-Tracker:在复杂环境中敏捷跟踪目标的鲁棒性空中系统_第12张图片](http://img.e-com-net.com/image/info8/09ebf71c05ac4518a4e7991ba728c39b.jpg)
2.2 最优时空轨迹生成
我们使用提出的高效优化方法生成分段多项式轨迹,参考Generating large-scale trajectories efficiently usingdouble descriptions of polynomials。
![[论文解读]Fast-Tracker:在复杂环境中敏捷跟踪目标的鲁棒性空中系统_第13张图片](http://img.e-com-net.com/image/info8/1e87d04a7d0145139074f9b4afe87960.jpg)
二、实验结果
1. 实验平台
实验在四旋翼平台上进行(如图7所示)。目标设置为携带二维码标签移动的人。我们使用视觉基准系统AprilTag来检测二维码标签。此外,还有三个摄像机组成的FOV摄像机阵列来检测目标。 由于视场角较宽,所以无人机不必面对目标。我们将无人机设计成面向跟踪轨迹的切线方向,以确保可以完全观察到周围的障碍物。系统总运行时间约为20毫秒。整个系统的重规划频率设置为15Hz,足以满足大多数跟踪任务的需求。
![[论文解读]Fast-Tracker:在复杂环境中敏捷跟踪目标的鲁棒性空中系统_第17张图片](http://img.e-com-net.com/image/info8/3a9097a2a7b4407ababe728d0d26502e.jpg)
2. 实际场景测试
室内室外测试,目标以1.3m的平均速度移动,无人机的跟踪速度达到3m/s。
![[论文解读]Fast-Tracker:在复杂环境中敏捷跟踪目标的鲁棒性空中系统_第18张图片](http://img.e-com-net.com/image/info8/03ac41a246594406b56fde556dda2140.jpg)
Fast-Tracker: A Robust Aerial System for Tracking Agile Target
三、总结
在本文中,我们提出了一种用于无人机空中跟随的系统解决方案。首先,提出了一种利用过去的目标观测来预测未来目标运动的目标运动预测方法。接着,我们提出一种基于启发式运动动力学的路径搜索器,并基于目标运动预测在密集环境中搜索出安全的跟踪轨迹。最后,将其优化为安全且动态可行的轨迹。所提出的方法已集成到具有考虑许多工程因素的机载四旋翼无人机系统中。大量的实验和基准对比确认了所提出系统的高效行、有效性以及鲁棒性。
将来,我们将专注于在跟踪任务期间实现动态避障。此外,我们将改进对象检测方法,使所提出的系统适用于更广义的场景。
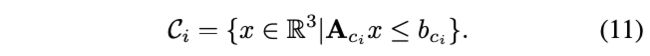

![[论文解读]Fast-Tracker:在复杂环境中敏捷跟踪目标的鲁棒性空中系统_第14张图片](http://img.e-com-net.com/image/info8/5ad65d27bbd14ea7bd6edc534b7ef0f3.jpg)
![[论文解读]Fast-Tracker:在复杂环境中敏捷跟踪目标的鲁棒性空中系统_第15张图片](http://img.e-com-net.com/image/info8/3186364bb421447cb5343efd782fdff2.jpg)
![[论文解读]Fast-Tracker:在复杂环境中敏捷跟踪目标的鲁棒性空中系统_第16张图片](http://img.e-com-net.com/image/info8/988f0d8c01fe416788687da8c6de2838.jpg)