【opencv4.3.0教程】04之基础结构及其常用功能介绍1
目录
一、前言
二、OpenCV基础结构
0、引入
1、基础结构都有啥
2、类型简述
0.介绍
1.Complex
2.Point_
3.Point3_
4.Size_
5.Rect_
6.RotatedRect
7.Range
8.Scalar_
9.KeyPoint
10.DMatch
11.TermCriteria
三、Point_
1、定义
1.构造函数
2.基本操作
3.成员变量
4.使用时的数据类型
2、常用方法
1.构造函数
2.常用基本操作
四、Size_
1、定义
1.构造函数
2.基本操作
3.成员变量
4.使用时的数据类型
2、常用方法
1.构造函数
2.常用基本操作
重要!说在后面的话
一、前言
上一篇文章,我们讲了Mat类,Mat类是最重要的基础结构,没有之一,因为所有的操作,都是基于你先定义了一个Mat类,然后再做深入操作。但是在OpenCV中,不仅仅有Mat类一个基础结构。
除了Mat类之外,还有哪些基础结构,他们有哪些基本用法呢?接下来就跟我一起走进这节课,来了解更多的基础结构吧!
给大家的小建议:
这一部分其实在后面的使用中并不是特别的重要,但是作为讲解,必须要放在这里讲解,如果你是初学者,你可以跳过这一部分的内容。
所以,对这一部分的内容,推荐这几种方式阅读:
1.兴趣了解,看一下,了解一下;
2.学到后面,用到一个没有见过的类型,过来看一下,理解一下;
3.已经对OpenCV有一定认知基础,过来巩固一下知识;
4.比较深入了解OpenCV,通过阅读基本类型,能够通过阅读本文构建一个更为完整的框架;
5.OpenCV大牛,对本文内容批评指正。
二、OpenCV基础结构
0、引入
在上一节内容中,我们讲到了OpenCV最基本的结构,也是最常用的结构Mat,在使用Mat的过程中,我们还涉及到了如下几个结构:
const Rect& roi;
const Range* ranges;
const Point_<_Tp>& pt;
const Point3_<_Tp>& pt;
const Scalar& s;啥?
你敢说我没讲?
回去好好看看上一篇博客去!
1、基础结构都有啥
当然结构不只有这些,那基础结构都有啥呢?
让我们打开OpenCV,找到types.hpp文件,看一下描述:
/*M///
//
// IMPORTANT: READ BEFORE DOWNLOADING, COPYING, INSTALLING OR USING.
//
// By downloading, copying, installing or using the software you agree to this license.
// If you do not agree to this license, do not download, install,
// copy or use the software.
//
//
// License Agreement
// For Open Source Computer Vision Library
//
// Copyright (C) 2000-2008, Intel Corporation, all rights reserved.
// Copyright (C) 2009, Willow Garage Inc., all rights reserved.
// Copyright (C) 2013, OpenCV Foundation, all rights reserved.
// Third party copyrights are property of their respective owners.
//
// Redistribution and use in source and binary forms, with or without modification,
// are permitted provided that the following conditions are met:
//
// * Redistribution's of source code must retain the above copyright notice,
// this list of conditions and the following disclaimer.
//
// * Redistribution's in binary form must reproduce the above copyright notice,
// this list of conditions and the following disclaimer in the documentation
// and/or other materials provided with the distribution.
//
// * The name of the copyright holders may not be used to endorse or promote products
// derived from this software without specific prior written permission.
//
// This software is provided by the copyright holders and contributors "as is" and
// any express or implied warranties, including, but not limited to, the implied
// warranties of merchantability and fitness for a particular purpose are disclaimed.
// In no event shall the Intel Corporation or contributors be liable for any direct,
// indirect, incidental, special, exemplary, or consequential damages
// (including, but not limited to, procurement of substitute goods or services;
// loss of use, data, or profits; or business interruption) however caused
// and on any theory of liability, whether in contract, strict liability,
// or tort (including negligence or otherwise) arising in any way out of
// the use of this software, even if advised of the possibility of such damage.
//
//M*/好吧,其实这个并不是很重要,重要的是下面,让我们一起走进这些基础结构,首先我们看一下这些基础结构的描述。
#include
#include
#include
#include
#include "opencv2/core/cvdef.h"
#include "opencv2/core/cvstd.hpp"
#include "opencv2/core/matx.hpp"
namespace cv
{
//! @addtogroup core_basic
//! @{
Complex //
/** @brief A complex number class.
The template class is similar and compatible with std::complex, however it provides slightly
more convenient access to the real and imaginary parts using through the simple field access, as opposite
to std::complex::real() and std::complex::imag().
*/
Point_
/** @brief Template class for 2D points specified by its coordinates `x` and `y`.
An instance of the class is interchangeable with C structures, CvPoint and CvPoint2D32f . There is
also a cast operator to convert point coordinates to the specified type. The conversion from
floating-point coordinates to integer coordinates is done by rounding. Commonly, the conversion
uses this operation for each of the coordinates. Besides the class members listed in the
declaration above, the following operations on points are implemented:
@code
pt1 = pt2 + pt3;
pt1 = pt2 - pt3;
pt1 = pt2 * a;
pt1 = a * pt2;
pt1 = pt2 / a;
pt1 += pt2;
pt1 -= pt2;
pt1 *= a;
pt1 /= a;
double value = norm(pt); // L2 norm
pt1 == pt2;
pt1 != pt2;
@endcode
For your convenience, the following type aliases are defined:
@code
typedef Point_ Point2i;
typedef Point2i Point;
typedef Point_ Point2f;
typedef Point_ Point2d;
@endcode
Example:
@code
Point2f a(0.3f, 0.f), b(0.f, 0.4f);
Point pt = (a + b)*10.f;
cout << pt.x << ", " << pt.y << endl;
@endcode
*/
Point3_
/** @brief Template class for 3D points specified by its coordinates `x`, `y` and `z`.
An instance of the class is interchangeable with the C structure CvPoint2D32f . Similarly to
Point_ , the coordinates of 3D points can be converted to another type. The vector arithmetic and
comparison operations are also supported.
The following Point3_\<\> aliases are available:
@code
typedef Point3_ Point3i;
typedef Point3_ Point3f;
typedef Point3_ Point3d;
@endcode
@see cv::Point3i, cv::Point3f and cv::Point3d
*/
Size_
/** @brief Template class for specifying the size of an image or rectangle.
The class includes two members called width and height. The structure can be converted to and from
the old OpenCV structures CvSize and CvSize2D32f . The same set of arithmetic and comparison
operations as for Point_ is available.
OpenCV defines the following Size_\<\> aliases:
@code
typedef Size_ Size2i;
typedef Size2i Size;
typedef Size_ Size2f;
@endcode
*/
Rect_
/** @brief Template class for 2D rectangles
described by the following parameters:
- Coordinates of the top-left corner. This is a default interpretation of Rect_::x and Rect_::y
in OpenCV. Though, in your algorithms you may count x and y from the bottom-left corner.
- Rectangle width and height.
OpenCV typically assumes that the top and left boundary of the rectangle are inclusive, while the
right and bottom boundaries are not. For example, the method Rect_::contains returns true if
\f[x \leq pt.x < x+width,
y \leq pt.y < y+height\f]
Virtually every loop over an image ROI in OpenCV (where ROI is specified by Rect_\ ) is
implemented as:
@code
for(int y = roi.y; y < roi.y + roi.height; y++)
for(int x = roi.x; x < roi.x + roi.width; x++)
{
// ...
}
@endcode
In addition to the class members, the following operations on rectangles are implemented:
- \f$\texttt{rect} = \texttt{rect} \pm \texttt{point}\f$ (shifting a rectangle by a certain offset)
- \f$\texttt{rect} = \texttt{rect} \pm \texttt{size}\f$ (expanding or shrinking a rectangle by a
certain amount)
- rect += point, rect -= point, rect += size, rect -= size (augmenting operations)
- rect = rect1 & rect2 (rectangle intersection)
- rect = rect1 | rect2 (minimum area rectangle containing rect1 and rect2 )
- rect &= rect1, rect |= rect1 (and the corresponding augmenting operations)
- rect == rect1, rect != rect1 (rectangle comparison)
This is an example how the partial ordering on rectangles can be established (rect1 \f$\subseteq\f$
rect2):
@code
template inline bool
operator <= (const Rect_<_Tp>& r1, const Rect_<_Tp>& r2)
{
return (r1 & r2) == r1;
}
@endcode
For your convenience, the Rect_\<\> alias is available: cv::Rect
*/
/ RotatedRect /
/** @brief The class represents rotated (i.e. not up-right) rectangles on a plane.
Each rectangle is specified by the center point (mass center), length of each side (represented by
#Size2f structure) and the rotation angle in degrees.
The sample below demonstrates how to use RotatedRect:
@snippet snippets/core_various.cpp RotatedRect_demo

@sa CamShift, fitEllipse, minAreaRect, CvBox2D
*/
Range /
/** @brief Template class specifying a continuous subsequence (slice) of a sequence.
The class is used to specify a row or a column span in a matrix ( Mat ) and for many other purposes.
Range(a,b) is basically the same as a:b in Matlab or a..b in Python. As in Python, start is an
inclusive left boundary of the range and end is an exclusive right boundary of the range. Such a
half-opened interval is usually denoted as \f$[start,end)\f$ .
The static method Range::all() returns a special variable that means "the whole sequence" or "the
whole range", just like " : " in Matlab or " ... " in Python. All the methods and functions in
OpenCV that take Range support this special Range::all() value. But, of course, in case of your own
custom processing, you will probably have to check and handle it explicitly:
@code
void my_function(..., const Range& r, ....)
{
if(r == Range::all()) {
// process all the data
}
else {
// process [r.start, r.end)
}
}
@endcode
*/
Scalar_ ///
/** @brief Template class for a 4-element vector derived from Vec.
Being derived from Vec\<_Tp, 4\> , Scalar\_ and Scalar can be used just as typical 4-element
vectors. In addition, they can be converted to/from CvScalar . The type Scalar is widely used in
OpenCV to pass pixel values.
*/
/// KeyPoint
/** @brief Data structure for salient point detectors.
The class instance stores a keypoint, i.e. a point feature found by one of many available keypoint
detectors, such as Harris corner detector, #FAST, %StarDetector, %SURF, %SIFT etc.
The keypoint is characterized by the 2D position, scale (proportional to the diameter of the
neighborhood that needs to be taken into account), orientation and some other parameters. The
keypoint neighborhood is then analyzed by another algorithm that builds a descriptor (usually
represented as a feature vector). The keypoints representing the same object in different images
can then be matched using %KDTree or another method.
*/
DMatch /
/** @brief Class for matching keypoint descriptors
query descriptor index, train descriptor index, train image index, and distance between
descriptors.
*/
/ TermCriteria //
/** @brief The class defining termination criteria for iterative algorithms.
You can initialize it by default constructor and then override any parameters, or the structure may
be fully initialized using the advanced variant of the constructor.
*/
//! @} core_basic
/ raster image moments //
//! @addtogroup imgproc_shape
//! @{
/** @brief struct returned by cv::moments
The spatial moments \f$\texttt{Moments::m}_{ji}\f$ are computed as:
\f[\texttt{m} _{ji}= \sum _{x,y} \left ( \texttt{array} (x,y) \cdot x^j \cdot y^i \right )\f]
The central moments \f$\texttt{Moments::mu}_{ji}\f$ are computed as:
\f[\texttt{mu} _{ji}= \sum _{x,y} \left ( \texttt{array} (x,y) \cdot (x - \bar{x} )^j \cdot (y - \bar{y} )^i \right )\f]
where \f$(\bar{x}, \bar{y})\f$ is the mass center:
\f[\bar{x} = \frac{\texttt{m}_{10}}{\texttt{m}_{00}} , \; \bar{y} = \frac{\texttt{m}_{01}}{\texttt{m}_{00}}\f]
The normalized central moments \f$\texttt{Moments::nu}_{ij}\f$ are computed as:
\f[\texttt{nu} _{ji}= \frac{\texttt{mu}_{ji}}{\texttt{m}_{00}^{(i+j)/2+1}} .\f]
@note
\f$\texttt{mu}_{00}=\texttt{m}_{00}\f$, \f$\texttt{nu}_{00}=1\f$
\f$\texttt{nu}_{10}=\texttt{mu}_{10}=\texttt{mu}_{01}=\texttt{mu}_{10}=0\f$ , hence the values are not
stored.
The moments of a contour are defined in the same way but computed using the Green's formula (see
). So, due to a limited raster resolution, the moments
computed for a contour are slightly different from the moments computed for the same rasterized
contour.
@note
Since the contour moments are computed using Green formula, you may get seemingly odd results for
contours with self-intersections, e.g. a zero area (m00) for butterfly-shaped contours.
*/ 2、类型简述
0.介绍
在这里给大家简单介绍一下这里的一些类,了解一下他们是做什么的。
1.Complex
第一个是一个复数类,这个比较简单,学过高中数学的,对其基本内容也比较清楚,没有什么太多要说明的,不常用。
2.Point_
这个算是OpenCV中比较基础的类了,表示的是二维点,既然是二维点,我们就一般使用两个坐标x和y来表示。我们能想到的有关于二维点集的操作,基本上在这里都有实现,在后面,我们还会详细说明。
3.Point3_
这个表示的也是点,表示的是三维点它的常用类型有:
typedef Point3_ Point3i;
typedef Point3_ Point3f;
typedef Point3_ Point3d; 在后面,我们详细讲解二维点的时候,我们发现它的定义是:
typedef Point_ Point2i;
typedef Point_ Point2l;
typedef Point_ Point2f;
typedef Point_ Point2d;
typedef Point2i Point; 通过这个对比,我们就能知道这里面的2表示的是二维,3表示的是三维。
4.Size_
这个是用于指定图像或矩形大小的简短模板类。这个也是我们经常会使用到的,这个类包括两个成员变量:width和height,表示图像或者矩阵的大小。在后面我们也会详细讲解。
5.Rect_
这个用于描述二维矩形,主要有两个部分的参数:
1.图像矩阵的左上角坐标。
2.图像矩阵的宽度和高度。
这个类型相比较上面的类型多了定位功能。
6.RotatedRect
上面表示的矩形是横平竖直的矩形,但是我们生活中遇到的矩形可能是歪着的,这个类表示的就是带有旋转角度的矩形。既然如此,那它的参数也就增加了。
因为是带有旋转角度,所以它的定位点,不再是左上角点,而是中心点,然后有四条边的长度(Size2f类型),还有最重要的旋转角度。
RotatedRect(const Point2f& center, const Size2f& size, float angle);我们也知道,如果一个矩形,我们给定了三个顶点,另外一个顶点的坐标也就知道了,所以在具体使用中,还有一种构造方式:
RotatedRect(const Point2f& point1, const Point2f& point2, const Point2f& point3);7.Range
这个是用于指定序列的连续子序列(切片)的模板类。重点在于,这个指定序列是什么?其实就是我们上一部分讲的Mat,虽然它是一个二维矩阵,但是它在存储的过程中是以一维数组的方式存储的。如果你学过python的话,这个跟python的range是类似的。只不过python中的可以设置步长,这个是连续的,也就是步长固定为1。
它最常用的构造函数如下:
Range::Range(int _start, int _end)8.Scalar_
这个也算是OpenCV中比较基础的类了,简单一点来说,我们一般用这个类来定义像素值,比如:
Scalar(0, 0, 255); //红色
Scalar(0, 255, 0); //绿色
Scalar(255, 0, 0); //蓝色在后面我们还会详细讲到,所以在这里就不过多说明啦!
9.KeyPoint
首先我们翻译一下这个名字,叫:关键点。这个是角点检测器的结构。由许多可用的关键点检测器之一找到的点特征,例如Harris角检测器等等。
在后面实战中,还会给大家介绍到。
10.DMatch
这个和上面的KeyPoint算是一个类型的,他们都是用作特征匹配的。这个类别用于查询描述符索引、列车描述符索引、列车图像索引和描述符之间的距离。
11.TermCriteria
这个是定义迭代算法终止条件的类。我们可以使用默认构造函数初始化它,然后重写任何参数,或者可以使用构造函数的高级变量完全初始化结构。
上面那个是整体介绍,主要是让大家能够简单了解都有哪些东西,确实太多啦,所以在这里,给大家讲解一下常用的成员及方法。其他没有讲到的,在后面使用中,我们还会逐步详细说明。
三、Point_
首先我们必须要讲的是Point_,这个是二维图像中非常基本的类了,就包括小学生也知道:
点构成线,线构成面,面构成体。
让我们从定义出发,一步一步来了解它吧!
1、定义
首先,我们要先看一下它的定义,定义如下:
template class Point_
{
public:
typedef _Tp value_type;
//! default constructor
Point_();
Point_(_Tp _x, _Tp _y);
Point_(const Point_& pt);
Point_(Point_&& pt) CV_NOEXCEPT;
Point_(const Size_<_Tp>& sz);
Point_(const Vec<_Tp, 2>& v);
Point_& operator = (const Point_& pt);
Point_& operator = (Point_&& pt) CV_NOEXCEPT;
//! conversion to another data type
template operator Point_<_Tp2>() const;
//! conversion to the old-style C structures
operator Vec<_Tp, 2>() const;
//! dot product
_Tp dot(const Point_& pt) const;
//! dot product computed in double-precision arithmetics
double ddot(const Point_& pt) const;
//! cross-product
double cross(const Point_& pt) const;
//! checks whether the point is inside the specified rectangle
bool inside(const Rect_<_Tp>& r) const;
_Tp x; //!< x coordinate of the point
_Tp y; //!< y coordinate of the point
};
typedef Point_ Point2i;
typedef Point_ Point2l;
typedef Point_ Point2f;
typedef Point_ Point2d;
typedef Point2i Point;
template class DataType< Point_<_Tp> >
{
public:
typedef Point_<_Tp> value_type;
typedef Point_::work_type> work_type;
typedef _Tp channel_type;
enum { generic_type = 0,
channels = 2,
fmt = traits::SafeFmt::fmt + ((channels - 1) << 8)
#ifdef OPENCV_TRAITS_ENABLE_DEPRECATED
,depth = DataType::depth
,type = CV_MAKETYPE(depth, channels)
#endif
};
typedef Vec vec_type;
};
namespace traits {
template
struct Depth< Point_<_Tp> > { enum { value = Depth<_Tp>::value }; };
template
struct Type< Point_<_Tp> > { enum { value = CV_MAKETYPE(Depth<_Tp>::value, 2) }; };
} // namespace
这里面最基本的定义主要包括如下三部分:
1.构造函数
几个构造函数,用于生成Point对象:
//! default constructor
Point_();
Point_(_Tp _x, _Tp _y);
Point_(const Point_& pt);
Point_(Point_&& pt) CV_NOEXCEPT;
Point_(const Size_<_Tp>& sz);
Point_(const Vec<_Tp, 2>& v);2.基本操作
几个基本操作,具体含义及其定义方式如下:
//! 两个赋值运算符
Point_& operator = (const Point_& pt);
Point_& operator = (Point_&& pt) CV_NOEXCEPT;
//! 点积
_Tp dot(const Point_& pt) const;
//! 双精度算法计算点积
double ddot(const Point_& pt) const;
//! 交叉积
double cross(const Point_& pt) const;
//! 检查点是否在指定的矩形内
bool inside(const Rect_<_Tp>& r) const;
3.成员变量
两个类体成员变量,大家肯定也能知道,就是两个坐标值:
_Tp x; //!< x coordinate of the point
_Tp y; //!< y coordinate of the point
4.使用时的数据类型
当我们定义了Point_类之后,我们要根据点的数据定义其具体使用时候的数据类型:
typedef Point_ Point2i;
typedef Point_ Point2l;
typedef Point_ Point2f;
typedef Point_ Point2d;
typedef Point2i Point;
其中,前四个指定 了Point_类的数据,分别是int,int64,float,double,在一般情况下,我们都会使用int类型的Point_,所以我们默认Point2i为Point。
2、常用方法
接下来我们要说的就是常用成员,它的全部成员函数还是很多的,我们只讲最常用的几个,为了方便大家快速理解,我们分类说明。
1.构造函数
构造函数如下:
template inline
Point_<_Tp>::Point_()
: x(0), y(0) {}
template inline
Point_<_Tp>::Point_(_Tp _x, _Tp _y)
: x(_x), y(_y) {}
template inline
Point_<_Tp>::Point_(const Point_& pt)
: x(pt.x), y(pt.y) {}
template inline
Point_<_Tp>::Point_(Point_&& pt) CV_NOEXCEPT
: x(std::move(pt.x)), y(std::move(pt.y)) {}
template inline
Point_<_Tp>::Point_(const Size_<_Tp>& sz)
: x(sz.width), y(sz.height) {}
template inline
Point_<_Tp>::Point_(const Vec<_Tp,2>& v)
: x(v[0]), y(v[1]) {} 最基本的构造函数,就是构造一个空的点,然后将坐标置为(0,0)。
Point p1 = Point();然后我们最常用的一个是使用两个点的坐标来创建一个点。
Point p2 = Point(1, 2);最基本的构造函数,就是构造一个空的点,然后将坐标置为(0,0)。
Point p3 = Point(p2);我们可以将上面的点输出,也可以访问点的两个坐标,代码和结果如下:
cout << "p1 = " << p1 << endl;
cout << "p1 = " << p2 << endl;
cout << "p3 = " << p3 << endl;
cout << "p3.x = " << p3.x << " , p3.y = " << p3.y << endl;2.常用基本操作
常用基本操作主要包括两个点的运算(包括以点表示的向量的运算,比如点(1,2)表示向量(1,2)),点的数乘运算等等,具体如下:
template inline
Point_<_Tp>& Point_<_Tp>::operator = (Point_&& pt) CV_NOEXCEPT
{
x = std::move(pt.x); y = std::move(pt.y);
return *this;
}
template template inline
Point_<_Tp>::operator Point_<_Tp2>() const
{
return Point_<_Tp2>(saturate_cast<_Tp2>(x), saturate_cast<_Tp2>(y));
}
template inline
Point_<_Tp>::operator Vec<_Tp, 2>() const
{
return Vec<_Tp, 2>(x, y);
}
template inline
_Tp Point_<_Tp>::dot(const Point_& pt) const
{
return saturate_cast<_Tp>(x*pt.x + y*pt.y);
}
template inline
double Point_<_Tp>::ddot(const Point_& pt) const
{
return (double)x*(double)(pt.x) + (double)y*(double)(pt.y);
}
template inline
double Point_<_Tp>::cross(const Point_& pt) const
{
return (double)x*pt.y - (double)y*pt.x;
}
template inline bool
Point_<_Tp>::inside( const Rect_<_Tp>& r ) const
{
return r.contains(*this);
}
template static inline
Point_<_Tp>& operator += (Point_<_Tp>& a, const Point_<_Tp>& b)
{
a.x += b.x;
a.y += b.y;
return a;
}
template static inline
Point_<_Tp>& operator -= (Point_<_Tp>& a, const Point_<_Tp>& b)
{
a.x -= b.x;
a.y -= b.y;
return a;
}
template static inline
Point_<_Tp>& operator *= (Point_<_Tp>& a, int b)
{
a.x = saturate_cast<_Tp>(a.x * b);
a.y = saturate_cast<_Tp>(a.y * b);
return a;
}
template static inline
Point_<_Tp>& operator *= (Point_<_Tp>& a, float b)
{
a.x = saturate_cast<_Tp>(a.x * b);
a.y = saturate_cast<_Tp>(a.y * b);
return a;
}
template static inline
Point_<_Tp>& operator *= (Point_<_Tp>& a, double b)
{
a.x = saturate_cast<_Tp>(a.x * b);
a.y = saturate_cast<_Tp>(a.y * b);
return a;
}
template static inline
Point_<_Tp>& operator /= (Point_<_Tp>& a, int b)
{
a.x = saturate_cast<_Tp>(a.x / b);
a.y = saturate_cast<_Tp>(a.y / b);
return a;
}
template static inline
Point_<_Tp>& operator /= (Point_<_Tp>& a, float b)
{
a.x = saturate_cast<_Tp>(a.x / b);
a.y = saturate_cast<_Tp>(a.y / b);
return a;
}
template static inline
Point_<_Tp>& operator /= (Point_<_Tp>& a, double b)
{
a.x = saturate_cast<_Tp>(a.x / b);
a.y = saturate_cast<_Tp>(a.y / b);
return a;
}
template static inline
double norm(const Point_<_Tp>& pt)
{
return std::sqrt((double)pt.x*pt.x + (double)pt.y*pt.y);
}
template static inline
bool operator == (const Point_<_Tp>& a, const Point_<_Tp>& b)
{
return a.x == b.x && a.y == b.y;
}
template static inline
bool operator != (const Point_<_Tp>& a, const Point_<_Tp>& b)
{
return a.x != b.x || a.y != b.y;
}
template static inline
Point_<_Tp> operator + (const Point_<_Tp>& a, const Point_<_Tp>& b)
{
return Point_<_Tp>( saturate_cast<_Tp>(a.x + b.x), saturate_cast<_Tp>(a.y + b.y) );
}
template static inline
Point_<_Tp> operator - (const Point_<_Tp>& a, const Point_<_Tp>& b)
{
return Point_<_Tp>( saturate_cast<_Tp>(a.x - b.x), saturate_cast<_Tp>(a.y - b.y) );
}
template static inline
Point_<_Tp> operator - (const Point_<_Tp>& a)
{
return Point_<_Tp>( saturate_cast<_Tp>(-a.x), saturate_cast<_Tp>(-a.y) );
}
template static inline
Point_<_Tp> operator * (const Point_<_Tp>& a, int b)
{
return Point_<_Tp>( saturate_cast<_Tp>(a.x*b), saturate_cast<_Tp>(a.y*b) );
}
template static inline
Point_<_Tp> operator * (int a, const Point_<_Tp>& b)
{
return Point_<_Tp>( saturate_cast<_Tp>(b.x*a), saturate_cast<_Tp>(b.y*a) );
}
template static inline
Point_<_Tp> operator * (const Point_<_Tp>& a, float b)
{
return Point_<_Tp>( saturate_cast<_Tp>(a.x*b), saturate_cast<_Tp>(a.y*b) );
}
template static inline
Point_<_Tp> operator * (float a, const Point_<_Tp>& b)
{
return Point_<_Tp>( saturate_cast<_Tp>(b.x*a), saturate_cast<_Tp>(b.y*a) );
}
template static inline
Point_<_Tp> operator * (const Point_<_Tp>& a, double b)
{
return Point_<_Tp>( saturate_cast<_Tp>(a.x*b), saturate_cast<_Tp>(a.y*b) );
}
template static inline
Point_<_Tp> operator * (double a, const Point_<_Tp>& b)
{
return Point_<_Tp>( saturate_cast<_Tp>(b.x*a), saturate_cast<_Tp>(b.y*a) );
}
template static inline
Point_<_Tp> operator * (const Matx<_Tp, 2, 2>& a, const Point_<_Tp>& b)
{
Matx<_Tp, 2, 1> tmp = a * Vec<_Tp,2>(b.x, b.y);
return Point_<_Tp>(tmp.val[0], tmp.val[1]);
}
template static inline
Point3_<_Tp> operator * (const Matx<_Tp, 3, 3>& a, const Point_<_Tp>& b)
{
Matx<_Tp, 3, 1> tmp = a * Vec<_Tp,3>(b.x, b.y, 1);
return Point3_<_Tp>(tmp.val[0], tmp.val[1], tmp.val[2]);
}
template static inline
Point_<_Tp> operator / (const Point_<_Tp>& a, int b)
{
Point_<_Tp> tmp(a);
tmp /= b;
return tmp;
}
template static inline
Point_<_Tp> operator / (const Point_<_Tp>& a, float b)
{
Point_<_Tp> tmp(a);
tmp /= b;
return tmp;
}
template static inline
Point_<_Tp> operator / (const Point_<_Tp>& a, double b)
{
Point_<_Tp> tmp(a);
tmp /= b;
return tmp;
}
为什么这里有很多重载函数?
这里面有很多,因为涉及到具体类型,所以需要写很多重载函数,这也是函数多的原因,但是真正的没有几类。
比如实现乘法,乘法运算符的左右两边可能是点和数,也可能是数和点,数的类型可能是整型int,可能是单精度浮点型float,可能是双精度浮点型double。这些在具体实现都是要写清楚的。
下面我们举几个例子来讲解一下常用的几个方法:
比如上面我们说到了点的基本操作,在这里也有实现,我们先把这几个实现一下:
Point p2 = Point(1, 2);
Point p4 = Point(7, 8);
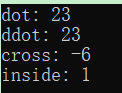
cout << "dot: " << p2.dot(p4) << endl;
cout << "ddot: " << p2.ddot(p4) << endl;
cout << "cross: " << p2.cross(p4) << endl;
cout << "inside: " << p2.inside(Rect(0, 0, 5, 5)) << endl;结果如下:
然后还有几个我们很熟悉的运算符,我们举几个例子:
Point p2 = Point(1, 2);
Point p3 = Point(p2);
if (p2 == p3) cout << "p2 == p3" << endl;
else cout << "p2 != p3" << endl;
cout << "norm(p2) = " << norm(p2) << endl;
cout << "p2 + p3 = " << p2 + p3 << endl;
cout << "p2 - p3 = " << p2 - p3 << endl;
cout << "p2 * 2 = " << p2 * 2 << endl;
cout << "p2 / 2 = " << p2 / 2 << endl;
四、Size_
接下来我们要讲的是Size_,这个表达的就是尺寸,在二维图像中,尺寸当然就是图像的长和宽啦!接下来让我们走进它吧!
1、定义
首先,我们要先看一下它的定义,定义如下:
template class Size_
{
public:
typedef _Tp value_type;
//! default constructor
Size_();
Size_(_Tp _width, _Tp _height);
Size_(const Size_& sz);
Size_(Size_&& sz) CV_NOEXCEPT;
Size_(const Point_<_Tp>& pt);
Size_& operator = (const Size_& sz);
Size_& operator = (Size_&& sz) CV_NOEXCEPT;
//! the area (width*height)
_Tp area() const;
//! aspect ratio (width/height)
double aspectRatio() const;
//! true if empty
bool empty() const;
//! conversion of another data type.
template operator Size_<_Tp2>() const;
_Tp width; //!< the width
_Tp height; //!< the height
};
typedef Size_ Size2i;
typedef Size_ Size2l;
typedef Size_ Size2f;
typedef Size_ Size2d;
typedef Size2i Size;
template class DataType< Size_<_Tp> >
{
public:
typedef Size_<_Tp> value_type;
typedef Size_::work_type> work_type;
typedef _Tp channel_type;
enum { generic_type = 0,
channels = 2,
fmt = DataType::fmt + ((channels - 1) << 8)
#ifdef OPENCV_TRAITS_ENABLE_DEPRECATED
,depth = DataType::depth
,type = CV_MAKETYPE(depth, channels)
#endif
};
typedef Vec vec_type;
};
namespace traits {
template
struct Depth< Size_<_Tp> > { enum { value = Depth<_Tp>::value }; };
template
struct Type< Size_<_Tp> > { enum { value = CV_MAKETYPE(Depth<_Tp>::value, 2) }; };
} // namespace 这里面最基本的定义主要包括如下三部分:
1.构造函数
几个构造函数,用于生成size对象:
//! default constructor
Size_();
Size_(_Tp _width, _Tp _height);
Size_(const Size_& sz);
Size_(Size_&& sz) CV_NOEXCEPT;
Size_(const Point_<_Tp>& pt);2.基本操作
几个基本操作,具体含义及其定义方式如下:
//! 两个赋值运算符
Size_& operator = (const Size_& sz);
Size_& operator = (Size_&& sz) CV_NOEXCEPT;
//! 面积 (width*height)
_Tp area() const;
//! 宽高比 (width/height)
double aspectRatio() const;
//! 判断是否为空
bool empty() const;3.成员变量
两个类体成员变量,大家肯定也能知道,就是宽高:
_Tp width; //!< the width
_Tp height; //!< the height4.使用时的数据类型
当我们定义了Size_类之后,我们要根据点的数据定义其具体使用时候的数据类型:
typedef Size_ Size2i;
typedef Size_ Size2l;
typedef Size_ Size2f;
typedef Size_ Size2d;
typedef Size2i Size; 其中,前四个指定 了Size_类的数据,分别是int,int64,float,double,在一般情况下,我们都会使用int类型的Size_,所以我们默认Size2i为Size。
2、常用方法
接下来我们要说的就是常用成员,它的全部成员函数还是很多的,我们只讲最常用的几个,为了方便大家快速理解,我们分类说明。
注:
大家会发现这个跟我们上面讲到Point类似,所以我们就不占字数进行代码举例啦,大家可以参考Point类的内容,如果有问题,可以随时跟我交流。
1.构造函数
构造函数如下:
template inline
Size_<_Tp>::Size_()
: width(0), height(0) {}
template inline
Size_<_Tp>::Size_(_Tp _width, _Tp _height)
: width(_width), height(_height) {}
template inline
Size_<_Tp>::Size_(const Size_& sz)
: width(sz.width), height(sz.height) {}
template inline
Size_<_Tp>::Size_(Size_&& sz) CV_NOEXCEPT
: width(std::move(sz.width)), height(std::move(sz.height)) {}
template inline
Size_<_Tp>::Size_(const Point_<_Tp>& pt)
: width(pt.x), height(pt.y) {}
template template inline
Size_<_Tp>::operator Size_<_Tp2>() const
{
return Size_<_Tp2>(saturate_cast<_Tp2>(width), saturate_cast<_Tp2>(height));
}
2.常用基本操作
常用基本操作主要包括基本赋值操作:
template inline
Size_<_Tp>& Size_<_Tp>::operator = (const Size_<_Tp>& sz)
{
width = sz.width; height = sz.height;
return *this;
}
template inline
Size_<_Tp>& Size_<_Tp>::operator = (Size_<_Tp>&& sz) CV_NOEXCEPT
{
width = std::move(sz.width); height = std::move(sz.height);
return *this;
} 类体内基本操作:
template inline
_Tp Size_<_Tp>::area() const
{
const _Tp result = width * height;
CV_DbgAssert(!std::numeric_limits<_Tp>::is_integer
|| width == 0 || result / width == height); // make sure the result fits in the return value
return result;
}
template inline
double Size_<_Tp>::aspectRatio() const
{
return width / static_cast(height);
}
template inline
bool Size_<_Tp>::empty() const
{
return width <= 0 || height <= 0;
}
运算符,包括赋值运算符(*=,/=,+=,-= ),四则运算符(+,-,*,/),等于不等于(==,!=)
template static inline
Size_<_Tp>& operator *= (Size_<_Tp>& a, _Tp b)
{
a.width *= b;
a.height *= b;
return a;
}
template static inline
Size_<_Tp> operator * (const Size_<_Tp>& a, _Tp b)
{
Size_<_Tp> tmp(a);
tmp *= b;
return tmp;
}
template static inline
Size_<_Tp>& operator /= (Size_<_Tp>& a, _Tp b)
{
a.width /= b;
a.height /= b;
return a;
}
template static inline
Size_<_Tp> operator / (const Size_<_Tp>& a, _Tp b)
{
Size_<_Tp> tmp(a);
tmp /= b;
return tmp;
}
template static inline
Size_<_Tp>& operator += (Size_<_Tp>& a, const Size_<_Tp>& b)
{
a.width += b.width;
a.height += b.height;
return a;
}
template static inline
Size_<_Tp> operator + (const Size_<_Tp>& a, const Size_<_Tp>& b)
{
Size_<_Tp> tmp(a);
tmp += b;
return tmp;
}
template static inline
Size_<_Tp>& operator -= (Size_<_Tp>& a, const Size_<_Tp>& b)
{
a.width -= b.width;
a.height -= b.height;
return a;
}
template static inline
Size_<_Tp> operator - (const Size_<_Tp>& a, const Size_<_Tp>& b)
{
Size_<_Tp> tmp(a);
tmp -= b;
return tmp;
}
template static inline
bool operator == (const Size_<_Tp>& a, const Size_<_Tp>& b)
{
return a.width == b.width && a.height == b.height;
}
template static inline
bool operator != (const Size_<_Tp>& a, const Size_<_Tp>& b)
{
return !(a == b);
} 重要!说在后面的话
哈,就先写到这里吧!因为确实是太多了,以至于博客温馨提醒,说读完可能需要一个小时让我删减内容。因为是讲基础,所以我得详细说一下,可能确实说的内容太多啦。
其实我纠结了一上午到底要不要写这一部分内容。
不写呢?这个东西是基础,在以后会经常用到,如果讲到了,就会很感觉很突兀。
写呢?确实不知道该怎么把握这个度。是要写成一本词典类型的吗?大可不必这样,这样既没有主次之分,又让整片博客太过于臃肿。还是讲几个重要的,把常用的说一下就好。但是这样讲的太简单了,觉得还是不太好。
所以我想了一下,要写,而且,要在上面两种写的方式取个折中。
从源码角度带领大家,整体看一下都有啥,了解了之后,将每种类型简单说明,让大家能够有个整体认识,能够知道都有哪几种类型,类型的含义是啥,表示的是什么数据。然后我们从中挑选出最常用的,详细讲解!从定义,方法,实战角度,全面了解。
学习之路,道阻且长!这个疫情,放慢了每个人的脚步,也让我想了很多,我研究生的方向,已经有所改变,跟计算机视觉可能没有直接关系了,但是,我喜欢,我还是想花一定的时间,放在这上面。
人,真的,要想想自己想要什么,愿不愿意为了喜欢的东西,去付出自己的时间和经历。曾经的我太年轻,没有坚持好好学数学,但这世上没有卖后悔药的,现在,我有了一个比较喜欢的东西,再难,我也要坚持下去!
我也希望大家能够借助疫情这次机会,静下心来,想想自己到底该做点什么,该怎么做?理想有时候很丰满,既然这么丰满,那我们为什么不努力去追寻一下呢?
正如开题的话!
我想:骨干的现实,会在追逐理想的我们面前屈服!